極座標による2重積分のとき，なぜ微小面積要素が $dx\, dy \rightarrow rdr\,d\theta$ となるのか。

2次元極座標とヤコビアン

2点 $P(x, y), \ Q(x + dx, y + dy)$ を考える。2点を結ぶベクトルは
$$ \overrightarrow{{PQ}} = dx \,\boldsymbol{i} + dy\, \boldsymbol{j}$$
ここで，$\boldsymbol{i}, \ \boldsymbol{j}$ はデカルト座標系の基本ベクトル。

一般に，2つのベクトルから作られる平行四辺形の面積はベクトルの外積を使って書けるから，この $\overrightarrow{{PQ}}$ を対角線とする平行四辺形の面積 $S$ は

$$ S = |dx\, \boldsymbol{i} \times dy\, \boldsymbol{j}| = dx\,dy\,|\boldsymbol{k}| = dx\,dy$$

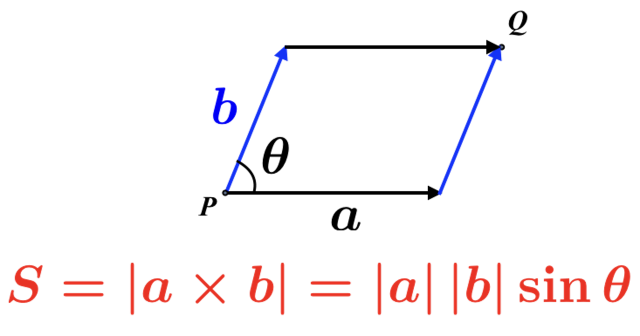
座標変換
\begin{eqnarray}x = x(r, \theta) = r\cos\theta, \quad y = y(r, \theta)=r\sin\theta
\end{eqnarray}
によって，
\begin{eqnarray}\overrightarrow{PQ} &=& dx \,\boldsymbol{i} + dy\, \boldsymbol{j}\\
&=& \left(\frac{\partial x}{\partial r} dr + \frac{\partial x}{\partial \theta} d\theta\right) \boldsymbol{i} +\left(\frac{\partial y}{\partial r} dr + \frac{\partial y}{\partial \theta} d\theta\right) \boldsymbol{j}\\
&=&dr \left(\frac{\partial x}{\partial r} \boldsymbol{i} + \frac{\partial y}{\partial r}\boldsymbol{j}\right) + d\theta \left(\frac{\partial x}{\partial \theta} \boldsymbol{i} + \frac{\partial y}{\partial \theta}\boldsymbol{j}\right) \\
&\equiv& dr \,\boldsymbol{e}_r + d\theta\, \boldsymbol{e}_{\theta}
\end{eqnarray}

したがって，$\overrightarrow{PQ}$ を対角線とする微小平行四辺形の面積 $dS$ を極座標で表すと，
\begin{eqnarray} dS &=& |dr\,\boldsymbol{e}_r \times d\theta\,\boldsymbol{e}_{\theta} |\\
&=& dr\,d\theta \left| \left(\frac{\partial x}{\partial r} \boldsymbol{i} + \frac{\partial y}{\partial r}\boldsymbol{j}\right)\times \left(\frac{\partial x}{\partial \theta} \boldsymbol{i} + \frac{\partial y}{\partial \theta}\boldsymbol{j}\right)\right|\\
&=& dr\,d\theta\left(\frac{\partial x}{\partial r} \frac{\partial y}{\partial \theta} – \frac{\partial y}{\partial r}\frac{\partial x}{\partial \theta}\right) |\boldsymbol{i} \times \boldsymbol{j}|\\
&=& dr\,d\theta\left(\frac{\partial x}{\partial r} \frac{\partial y}{\partial \theta} – \frac{\partial y}{\partial r}\frac{\partial x}{\partial \theta}\right) |\boldsymbol{k}|\\
&\equiv& dr\,d\theta \frac{\partial(x,y)}{\partial(r,\theta)}
\end{eqnarray}

ここで，$$ \frac{\partial(x,y)}{\partial(r,\theta)} \equiv
\begin{vmatrix}
\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\
\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta}\\
\end{vmatrix}
= \frac{\partial x}{\partial r} \frac{\partial y}{\partial \theta} – \frac{\partial y}{\partial r}\frac{\partial x}{\partial \theta}$$ をヤコビアンという。

極座標への変換の場合はヤコビアンが以下のように計算できて
$$\frac{\partial(x,y)}{\partial(r,\theta)} = \cos\theta\cdot r\,\sin\theta – \sin\theta\,\cdot (-r\,\sin\theta) = r$$
最終的に
$$ dS = dx\,dy = \frac{\partial(x,y)}{\partial(r,\theta)} dr\,d\theta = r\, dr\,d\theta$$ となる。

一般の2次元の座標変換 $x = x(u,v), \ y = y(u, v)$ に対しても
$$ dS = dx\,dy = \frac{\partial(x,y)}{\partial(u,v)} du\,dv$$

ということで，ヤコビアンというものが，ベクトルの外積が面積になるのだということと，合成関数の偏微分の規則から理解することができた。

3次元の座標変換とヤコビアン

また，3次元の座標変換 $x = x(u,v,w), \ y = y(u, v,w), \ z = z(u,v,w)$ についても，3つの線形独立なベクトル $\boldsymbol{a}, \ \boldsymbol{b}, \boldsymbol{c}$ から作られる立体（平行六面体）の体積 $V$ が

$$ V = \boldsymbol{a}\cdot(\boldsymbol{b}\times\boldsymbol{c})$$

であることを使うと，微小体積要素 $dV$ が

$$ dV = dx\,dy\,dz = \frac{\partial(x,y,z)}{\partial(u,v,w)} du\,dv\,dw$$

となることが示される。

微小変位ベクトル

$$d\boldsymbol{r} = dx \,\boldsymbol{i} + dy\,\boldsymbol{j} + dz\,\boldsymbol{k}$$

3本の（線形独立な）ベクトル $dx\, \boldsymbol{i}, \ dy\, \boldsymbol{j}, \ dz\,\boldsymbol{k}$ からつくられる微小な平行6面体の体積 $dV$ は

\begin{eqnarray}
dV &=& \left(dx\, \boldsymbol{i} \right) \cdot \left( \left(dy\, \boldsymbol{j} \right)\times\left(dz\,\boldsymbol{k} \right)\right) \\
&=& dx\,dy\, dz\, \boldsymbol{i} \cdot(\boldsymbol{j}\times\boldsymbol{k}) \\
&=& dx\,dy\, dz\, \boldsymbol{i} \cdot \boldsymbol{i} \\
&=& dx\,dy\, dz
\end{eqnarray}

一方，座標変換

\begin{eqnarray}
x &=& x(u, v, w) \\
y &=& y(u, v, w) \\
z &=& z(u, v, w) \\
\end{eqnarray}

により，全微分は

\begin{eqnarray}
dx &=& \frac{\partial x}{\partial u} du + \frac{\partial x}{\partial v} dv +\frac{\partial x}{\partial w} dw \\
dy &=& \frac{\partial y}{\partial u} du + \frac{\partial y}{\partial v} dv +\frac{\partial y}{\partial w} dw \\
dz &=& \frac{\partial z}{\partial u} du + \frac{\partial z}{\partial v} dv +\frac{\partial z}{\partial w} dw \\
\end{eqnarray}

となるから，微小変位ベクトルは以下のように書くことができる。

\begin{eqnarray}
d \boldsymbol{r}&=& dx \,\boldsymbol{i} + dy\,\boldsymbol{j} + dz\,\boldsymbol{k} \\
&=& \ \ \ \left(\frac{\partial x}{\partial u} du + \frac{\partial x}{\partial v} dv +\frac{\partial x}{\partial w} dw \right)\boldsymbol{i} \\
&& + \left(\frac{\partial y}{\partial u} du + \frac{\partial y}{\partial v} dv +\frac{\partial y}{\partial w} dw \right) \boldsymbol{j} \\
&& + \left(\frac{\partial z}{\partial u} du + \frac{\partial z}{\partial v} dv +\frac{\partial z}{\partial w} dw \right) \boldsymbol{k} \\
&=& du\, \boldsymbol{e}_u + dv\,\boldsymbol{e}_v + dw\, \boldsymbol{e}_w
\end{eqnarray}

ここで，

\begin{eqnarray}
\boldsymbol{e}_u&\equiv& \frac{\partial x}{\partial u} \boldsymbol{i} + \frac{\partial y}{\partial u} \boldsymbol{j} + \frac{\partial z}{\partial u} \boldsymbol{k} \\
\boldsymbol{e}_v&\equiv& \frac{\partial x}{\partial v} \boldsymbol{i} + \frac{\partial y}{\partial v} \boldsymbol{j} + \frac{\partial z}{\partial v} \boldsymbol{k} \\
\boldsymbol{e}_w&\equiv& \frac{\partial x}{\partial w} \boldsymbol{i} + \frac{\partial y}{\partial w} \boldsymbol{j} + \frac{\partial z}{\partial w} \boldsymbol{k}
\end{eqnarray}

ということで，体積要素 $dV$ は3本のベクトル $du\, \boldsymbol{e}_u,\ dv\,\boldsymbol{e}_v, \, dw\, \boldsymbol{e}_w$ からつくられる平行6面体の体積としても表されるから

\begin{eqnarray}
dV = dx\,dy\,dz = du\,dv\,dw \, \boldsymbol{e}_u \cdot(\boldsymbol{e}_v \times\boldsymbol{e}_w)
\end{eqnarray}

ベクトルのスカラー三重積は，3つのベクトルの成分を並べた $3\times 3$ 行列の（転置行列でも可）の行列式と等しいことはここでわかっているので

\begin{eqnarray}
\boldsymbol{e}_u \cdot(\boldsymbol{e}_v \times\boldsymbol{e}_w)
&=& \det \begin{pmatrix}
\frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} & \frac{\partial z}{\partial u} \\
\frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} & \frac{\partial z}{\partial v} \\
\frac{\partial x}{\partial w} & \frac{\partial y}{\partial w} & \frac{\partial z}{\partial w}
\end{pmatrix} \\
&=&
\det \begin{pmatrix}
\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w} \\
\frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w} \\
\frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w}
\end{pmatrix} \\
&=& \frac{\partial(x,y,z)}{\partial(u,v,z)}
\end{eqnarray}

したがって，

\begin{eqnarray}
dV = dx\,dy\,dz = \frac{\partial(x,y,z)}{\partial(u,v,z)} du\,dv\,dw
\end{eqnarray}

円筒座標とヤコビアン

\begin{eqnarray}
x &=& \rho \cos\phi \\
y &=& \rho \sin\phi \\
z &=& z
\end{eqnarray}

$$\frac{\partial(x,y,z)}{\partial(\rho, \phi, z)} =\frac{\partial(x,y)}{\partial(\rho, \phi)} = \rho$$

したがって

$$dV = \frac{\partial(x,y,z)}{\partial(\rho, \phi, z)} d\rho\,d\phi\, dz = \rho\, d\rho\,d\phi\, dz$$

極座標とヤコビアン

\begin{eqnarray}
x &=& r \sin\theta \cos\phi \\
y &=& r \sin\theta \sin\phi \\
z &=& r \cos\theta \\
\end{eqnarray}

$$\frac{\partial(x,y,z)}{\partial(r, \theta, \phi)} = r^2 \sin\theta$$

したがって

$$dV = \frac{\partial(x,y,z)}{\partial(r, \theta, \phi)} dr\, d\theta\, d\phi = r^2 dr\, \sin\theta\, d\theta\, d\phi$$

Maxima-Jupyter でヤコビアンの計算

2次元極座標とヤコビアン

\begin{eqnarray}
x &=& r\cos\phi \\
y &=& r\sin\phi
\end{eqnarray}

In [1]:

x: r * cos(phi);
y: r * sin(phi);

Out[1]:

\[\tag{${\it \%o}_{1}$}\cos \varphi\,r\]

Out[1]:

\[\tag{${\it \%o}_{2}$}\sin \varphi\,r\]

Maxima の jacobian() は「関数行列」であり，「関数行列式」にするにはさらに determinant() をとる必要がある。

In [2]:

determinant(jacobian([x,y], [r,phi]))$
trigsimp(%);

Out[2]:

\[\tag{${\it \%o}_{4}$}r\]

3次元円筒座標とヤコビアン

\begin{eqnarray}
x &=& \rho \cos\phi \\
y &=& \rho \sin\phi \\
z &=& z
\end{eqnarray}

In [3]:

x: rho * cos(phi);
y: rho * sin(phi);

Out[3]:

\[\tag{${\it \%o}_{5}$}\cos \varphi\,\rho\]

Out[3]:

\[\tag{${\it \%o}_{6}$}\sin \varphi\,\rho\]

In [4]:

determinant(jacobian([x,y,z], [rho,phi,z]))$
trigsimp(%);

Out[4]:

\[\tag{${\it \%o}_{8}$}\rho\]

3次元極座標とヤコビアン

\begin{eqnarray}
x &=& r\sin\theta \cos\phi \\
y &=& r\sin\theta \sin\phi \\
z &=& r \cos\theta
\end{eqnarray}

In [5]:

x: r * sin(theta) * cos(phi);
y: r * sin(theta) * sin(phi);
z: r * cos(theta);

Out[5]:

\[\tag{${\it \%o}_{9}$}\cos \varphi\,r\,\sin \vartheta\]

Out[5]:

\[\tag{${\it \%o}_{10}$}\sin \varphi\,r\,\sin \vartheta\]

Out[5]:

\[\tag{${\it \%o}_{11}$}r\,\cos \vartheta\]

In [6]:

determinant(jacobian([x,y,z], [r,theta,phi]))$
trigsimp(%);

Out[6]:

\[\tag{${\it \%o}_{13}$}r^2\,\sin \vartheta\]

参考：極座標による2重積分とヤコビアン

2次元極座標とヤコビアン

3次元の座標変換とヤコビアン

円筒座標とヤコビアン

極座標とヤコビアン

Maxima-Jupyter でヤコビアンの計算

2次元極座標とヤコビアン

3次元円筒座標とヤコビアン

3次元極座標とヤコビアン

このページの目次

このセクションの構成