$$I = \iint_D dx dy, \quad D: x^2 + y^2 \leq 1$$
\(\displaystyle I = \iint_D dx dy\) は領域 \(D\) の面積を表すのであった。 \(D: x^2 + y^2 \leq 1\) つまり,領域 \(D\) は半径 \(1\) の円の内部の面積であるから,半径 \(r\) の円の面積の公式 \(S = \pi r^2\) より \(I = \pi\) である。
では実際に \(\displaystyle \iint_{D} dx dy\) をどうやって計算するか,2つの方法を紹介する。
累次積分を使う
領域 \(D\) の条件式から,
$$D: x^2 + y^2 \leq 1 \quad \Rightarrow \quad y^2 \leq 1 – x^2 $$
$$\therefore -\sqrt{1-x^2} \leq y \leq \sqrt{1-x^2} $$
\begin{eqnarray}
I &=& \iint_{x^2 + y^2 \leq 1} dx dy \\
&=& \int_{-1}^{1} \left\{\int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} dy\right\} dx\\
&=& 2 \int_{-1}^1 \sqrt{1-x^2} dx
\end{eqnarray}
高校数学では,$y = f(x)$ と $y = g(x)$ が区間 $a \leq x \leq b$ で $f(x) \geq g(x)$ のとき,$y = f(x), \ y = g(x), \ x = a, \ x = b$ で囲まれる部分の面積 $S$ が
$$S = \int_a^b \left( f(x) – g(x) \right) \, dx$$
となると習ったと思うが,この式が上記の累次積分で導かれたことになる。
ここで,\(x = \sin\theta\) と変数変換すると,\(\sqrt{1-x^2} = \cos\theta, dx = \cos\theta d\theta\)。
\begin{eqnarray}
I &=& 2 \int_{-1}^1 \sqrt{1-x^2} dx \\
&=& 2 \int_{-\pi/2}^{\pi/2} \cos^2\theta d\theta\\
&=& \int_{-\pi/2}^{\pi/2} (1 + \cos 2\theta) d\theta \\
&=&\left[ \theta + \frac{1}{2}\sin 2\theta\right]_{-\pi/2}^{\pi/2} = \pi
\end{eqnarray}
$$\therefore I = \pi$$
極座標による2重積分
そもそも微小面積要素 \(dx dy\) とは,2点 \(P(x, y), \ Q(x + dx, y + dy)\) を対角線とする微小長方形の面積であった。これを極座標で表すと,\(P(r,\theta), \ Q(r + dr, \theta + d\theta)\) を対角線とする微小長方形の面積となり,\( dr \times r d\theta\) となる。
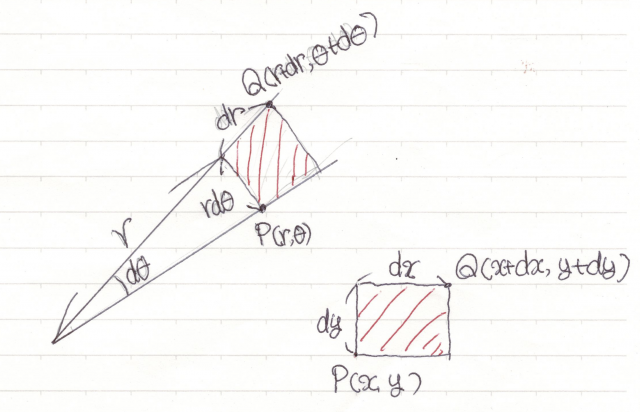
極座標で表すと,領域 \(D: x^2 + y^2 \leq 1\) は \(D: 0 \leq r \leq 1, \ 0 \leq \theta \leq 2\pi\) となる。つまり,
\begin{eqnarray} \iint_{D} dx dy
&=& \iint_D r dr \,d\theta \\
&=& \int_{0\leq \theta \leq 2\pi} \left\{\int_{0\leq r \leq 1} r dr\right\} d \theta\\
&=& \int_0^{2 \pi} d \theta \int_0^1 r dr \\
&=& 2\pi \times \left[\frac{r^2}{2}\right]_0^1 = \pi
\end{eqnarray}