例題
$\displaystyle \iint_D (2 + x)\, dx\, dy, \quad D: x^2 + y^2 \leq 1$
領域 $D$ は原点を中心とした半径 $1$ の円の内部であるから,
$$D: -1 \leq x \leq 1, \quad -\sqrt{1 -x^2} \leq y \leq \sqrt{1 -x^2}$$
したがって,累次積分の要領で
\begin{eqnarray}
\iint_D (2 + x) dx\, dy &=& \int_{-1}^1 dx \int_{-\sqrt{1 -x^2}}^{\sqrt{1 -x^2}} dy \, (2+x) \\
&=& \int_{-1}^1 dx\ (2 + x)\, \biggl[\,y\,\biggr]_{-\sqrt{1 -x^2}}^{\sqrt{1 -x^2}} \\
&=& \int_{-1}^1 dx \, (4 + 2 x) \sqrt{1 -x^2} \\
&=& 4 \int_{-1}^1 \sqrt{1 -x^2}\, dx + \int_{-1}^1 2 x \sqrt{1 -x^2}\, dx \\
&=& \cdots \\
&=& 2 \pi
\end{eqnarray}
(学生諸君はちゃんと定積分の部分を省略せずに計算過程を明示して計算するのですよ。)
この立体は,$z$ 軸を中心軸とした底面が半径 $1$ の円と,$z=2$ を含む平面 $z = f(x, y) = 2 + x$ で区切られた立体であるから…
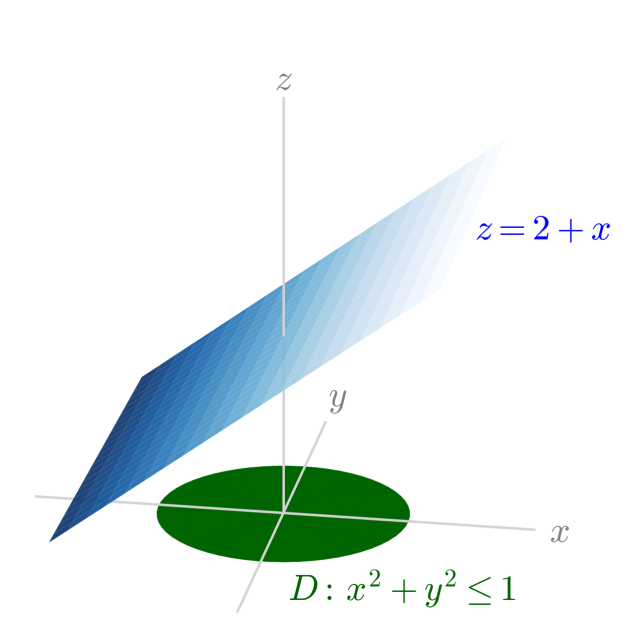
底面が半径 $1$ の円である円柱を,$z=2$ を含む平面 $z = f(x, y) = 2 + x$ で斜めに切ったものの下部の体積に相当する。
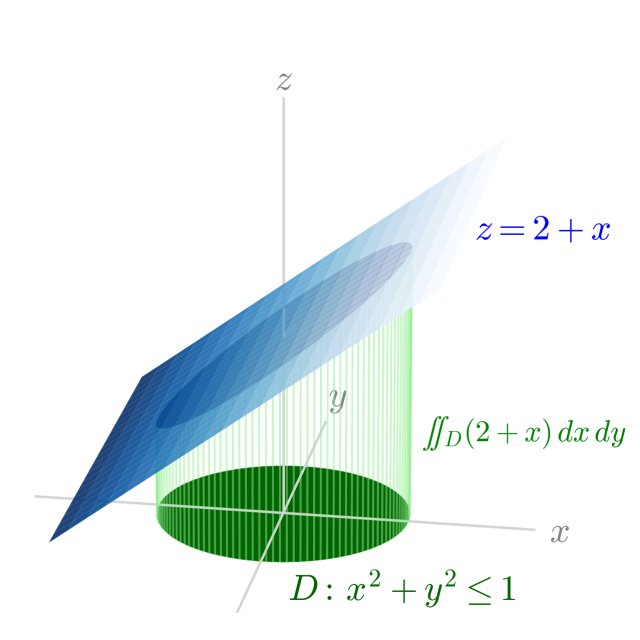
つまり,底面積が半径 $r=1$ の円の面積 $\pi\,r^2 = \pi$,高さが $h = 4$ の円柱の体積の半分であるから…
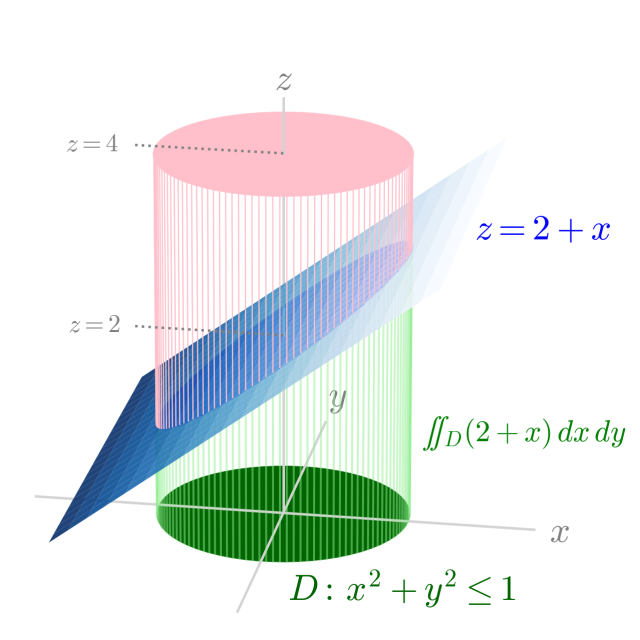
$$ V = \pi\,r^2 \times h \times \frac{1}{2} = 2 \pi$$
と,確かになっている。
