最後に，微分形で書かれているマクスウェル方程式を積分形で理解するために必要な，ベクトル場の積分公式についてまとめておきます。
多重積分：多変数関数の積分
1変数関数 $f(x)$ の積分は
$$\int_a^b f(x) dx$$
と書くのであった。電磁気学では1変数関数だけでなく，一般に空間座標 $x, y, z$ および時間座標 $y$ の4つの変数に依存する関数（多変数関数，スカラー場・ベクトル場）の積分が出てくる。このような多変数関数の積分のことを多重積分という。
2重積分・面積分
2変数関数 $f(x, y)$ の領域 $D$ での積分
$$\iint_D f(x, y) \ dx\, dy$$
は，多重積分のうちで特に2重積分と呼ばれる。面積要素 $dx\, dy$ は何も $xy$ 平面上に限らないので一般に$ dx\, dy \ \rightarrow \ dS$ と書いて
$$\iint_D f(x, y) \ dS$$
を「面積分」という。（「面積分」とすべきか「面積積分」とすべきは悩むところ。Wikipedia でも微妙にぶれていると思われ，2重積分は「面積分」なのに3重積分は「体積積分」としている。）
具体的な計算は，たとえば領域 $D$ が
$$D: x_1 \leq x \leq x_2, \ y_1 \leq y \leq y_2$$
であれば
\begin{eqnarray}
\iint_D f(x, y) \ dS &=&\iint_D f(x, y) \ dx\, dy \\
&=& \int_{y_1}^{y_2} \left\{\int_{x_1}^{x_2} f(x, y) \,dx \right\} dy
\end{eqnarray}
のように1変数ずつ積分していく。また，積分変数とその積分範囲（下端・上端）を明確にするために，以下のような記法も使われる。
\begin{eqnarray}
\iint_D f(x, y) \ dS &=&\iint_D f(x, y) \ dx\, dy \\
&=& \int_{y_1}^{y_2} dy \int_{x_1}^{x_2} dx \, f(x, y)
\end{eqnarray}
2次元極座標系の面積要素
領域 $D$ によっては，デカルト座標 $x, y$ よりも以下で定義される極座標 $\rho, \, \phi$ を使って積分したほうが便利な場合がある。（$r$ は3次元極座標の場合にとっておく。）
\begin{eqnarray}
x &=& \rho \cos\phi \\
y &=& \rho \sin\phi
\end{eqnarray}
この場合の面積要素 $dS$ は以下のようになることに注意。（「参考：極座標による2重積分とヤコビアン」のページを参照。）
$$dS = dx\, dy \Rightarrow \rho\, d\rho \,d\phi$$
3重積分・体積積分
3変数関数 $f(x, y, z)$ の領域 $V$ での積分
$$\iiint_V f(x, y, z) \ dx\, dy\, dz$$
は，多重積分のうちで特に3重積分と呼ばれる。体積要素 $dx\, dy\, dz$ は一般に$ dx\, dy\, dz \ \rightarrow \ dV$ と書いて
$$\iiint_V f(x, y, z) \, dV$$
を「体積積分」という。
具体的な計算は，たとえば領域 $V$ が
$$V: x_1 \leq x \leq x_2, \ y_1 \leq y \leq y_2, \ z_1 \leq z \leq z_2$$
であれば
\begin{eqnarray}
\iiint_V f(x, y, z) \, dV &=&\iiint_V f(x, y, z) \ dx\, dy\, dz\\
&=& \int_{z_1}^{z_2} \left\{ \int_{y_1}^{y_2} \left\{\int_{x_1}^{x_2} f(x, y, z) \,dx \right\} dy\right\} dz
\end{eqnarray}
のように1変数ずつ積分していく。また，積分変数とその積分範囲（下端・上端）を明確にするために，以下のような記法も使われる。
\begin{eqnarray}
\iiint_V f(x, y, z) \ dV &=&\iiint_V f(x, y, z) \ dx\, dy\, dz\\
&=& \int_{z_1}^{z_2} dz \int_{y_1}^{y_2} dy \int_{x_1}^{x_2} dx \, f(x, y, z)
\end{eqnarray}
3次元円筒座標系の体積要素
領域 $V$ によっては，デカルト座標 $x, y, z$ よりも以下で定義される円筒座標 $\rho, \, \phi, \,z$ を使って積分したほうが便利な場合がある。（$r$ は3次元極座標の場合にとっておく。）
\begin{eqnarray}
x &=& \rho \cos\phi \\
y &=& \rho \sin\phi \\
z &=& z
\end{eqnarray}
この場合の体積要素 $dV$ は以下のようになることに注意。（「参考：極座標による2重積分とヤコビアン」のページを参照。）
$$dV = dx\, dy\,dz \Rightarrow \rho\, d\rho \,d\phi\, dz$$
3次元極座標系の体積要素
領域 $V$ によっては，デカルト座標 $x, y, z$ よりも以下で定義される極座標 $r, \,\theta\, \phi$ を使って積分したほうが便利な場合がある。
\begin{eqnarray}
x &=& r \sin\theta \cos\phi \\
y &=& r \sin\theta \sin\phi \\
z &=& r \cos\theta
\end{eqnarray}
この場合の体積要素 $dV$ は以下のようになることに注意。
$$dV = dx\, dy\, dz \Rightarrow r^2 dr\, \sin\theta\, d\theta\, d\phi$$
勾配 grad の線積分
1変数関数 \( f(x) \) について，\( x \) から \(x + dx \) までの無限小変化分は（ \(dx \) の1次までとるとして）
$$df \equiv f(x + dx) -f(x) \simeq \frac{df}{dx} dx$$
したがって，\( x = x_1 \) から \( x = x_2 \) までの \( f(x) \) の変化分は以下のような積分で書ける。
$$ \int_{x_1}^{x_2} \frac{df}{dx} dx = f(x_2) -f(x_1)$$
多変数関数であるスカラー場 \( \varphi(x, y, z) \) の場合も同様に
\begin{eqnarray}
d\varphi &\equiv& \varphi(x+dx, y+dy, z + dz) -\varphi(x, y, z) \\
&=& \frac{\partial \varphi}{\partial x} dx + \frac{\partial \varphi}{\partial y} dy + \frac{\partial \varphi}{\partial z} dz \\
&\simeq& (\nabla \varphi)\cdot d\boldsymbol{r} \end{eqnarray}
ここで $$d\boldsymbol{r}
= dx \,\boldsymbol{i} + dy \,\boldsymbol{j} + dz \,\boldsymbol{k}$$
したがって，空間の点 \( \boldsymbol{r}_1 \) から点 \( \boldsymbol{r}_2 \) までの \( \varphi(\boldsymbol{r}) \) の変化分は以下のような線積分で書ける。
$$\int_{\boldsymbol{r}_1}^{\boldsymbol{r}_2} \nabla \varphi\cdot d\boldsymbol{r} = \int_{\boldsymbol{r}_1}^{\boldsymbol{r}_2} d\varphi = \varphi(\boldsymbol{r}_2) -\varphi(\boldsymbol{r}_1) $$
$d\boldsymbol{r}$ は $\boldsymbol{r}_1$ から $\boldsymbol{r}_2$ までを結ぶ曲線 $C$ にそった微小接ベクトルであるから，この線積分の値は曲線 $C$ の取り方に依存しそうなものだが，結果は，$\varphi(\boldsymbol{r}_2) -\varphi(\boldsymbol{r}_1)$ となり，2点の位置のみで決まり，2点を結ぶ曲線の取り方には依存しない。この理由は，もう少し後でストークスの定理を知ると理解できるようになる。
発散 div の体積積分と閉曲面を貫く外向きの全流速：ガウスの定理
ベクトル場 \( \boldsymbol{a} \) が，何か（エネルギーとか熱量とか）の単位面積あたりの流れを表すもの（流束密度ベクトル，この場合の「密度」とは「面密度」のこと）と想像しよう。
微小面積 \( dS \) を垂直に貫いて流れる量（流束）は，\( dS \) に垂直な単位ベクトル \( \boldsymbol{n} \) を使って \( \boldsymbol{a}\cdot\boldsymbol{n}\ dS \) となる。したがって，面積 \( S \) を垂直に貫いて流れる量（外向きの全流速）は
$$ \iint_S \boldsymbol{a}\cdot\boldsymbol{n} \ dS $$
ガウスの定理とは，ベクトル場の発散の体積についての積分に関する定理で以下のように書ける。
$$ \iiint_V \nabla\cdot \boldsymbol{a}\, dV = \iint_S \boldsymbol{a}\cdot\boldsymbol{n} \ dS $$ ここで，\( S \) は体積 \( V \) を囲む閉曲面である。
ガウスの定理を言葉で表すと，「ベクトル場の発散の体積積分（いわば体積 $V$ 内の全発散）は，その体積を囲む閉曲面を貫く外向きの全流速である」ということになる。
証明は別ページ「参考：ガウスの定理の証明」で。
ちなみに，「線積分」は「線積分」で問題ないが，ある量 \( f(x,y,z) \) の体積 \( V \) 内での積分
$$ \iiint_{V} f\, dxdydz, \quad \iiint_{V} f \,dV$$ などを「体積分」と呼ぶべきか「体積積分」と呼ぶべきか悩む。同様に，ある量 \( f(x,y,z) \) の面積 \( S \) 内での積分
$$ \iint_{S} f\ dx\, dy, \quad \iint_{S} f \ dS$$ などを「面積分」と呼ぶべきか「面積積分」と呼ぶべきかも少し悩む。
回転 rot の面積分と閉曲線に沿った循環：ストークスの定理
ベクトル場 \(\boldsymbol{a} \) の閉曲線 \(C \) に沿った成分をちょうど1周分線積分することを以下のように書く。
$$\oint_{C} \boldsymbol{a}\cdot d\boldsymbol{r} $$ この量を閉曲線（あるいはループ）\( C \) のまわりの循環と呼ぶ。
ストークスの定理とは，ベクトル場の回転の垂直成分の面積分に関する定理で以下のように書ける。
$$ \iint_{S} (\nabla\times \boldsymbol{a})\cdot \boldsymbol{n}\ dS = \oint_{C} \boldsymbol{a}\cdot d\boldsymbol{r} $$ ここで，\( S \) は閉曲線 \( C \) を縁とする任意の曲面である。単に閉曲線 \( C \) を縁とする曲面といっても無数にあると思うが，実は左辺の面積分はその曲面の取り方によらないことも示すことができる。
ストークスの定理を言葉で表すと，「ベクトル場の回転の垂直成分の面積分は，その面積の境界である閉曲線に沿った循環である」ということになる。
やはり証明は別ページ「参考：ストークスの定理の証明」で。
参考：勾配の線積分が経路の取り方に依存しないこと
さて，もしベクトル $\boldsymbol{a}$ があるスカラー関数 $\varphi$ の勾配 grad で書けるとしよう。そうすると，
\begin{eqnarray}
\boldsymbol{a} &\equiv& \nabla \varphi \\
\therefore \ \ \iint_{S} (\nabla\times (\nabla \varphi))\cdot \boldsymbol{n}\ dS &=& \oint_{C} (\nabla \varphi)\cdot d\boldsymbol{r}
\end{eqnarray}
ベクトル解析の恒等式
$$\nabla\times (\nabla \varphi) = \boldsymbol{0}$$
を使うと，
$$\oint_{C} (\nabla \varphi)\cdot d\boldsymbol{r} = 0$$
このことから，スカラー場 $\varphi(\boldsymbol{r})$ の勾配 $\nabla \varphi$ の線積分が経路によらずに，端点での値だけで決まることが以下のようにしてわかる。
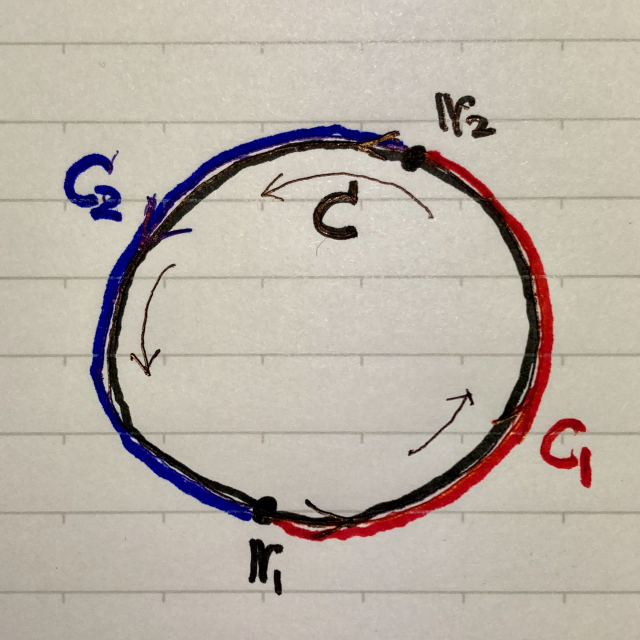
図のように，$\boldsymbol{r}_1$ から点 $\boldsymbol{r}_2$ までの曲線 ${\color{red}{C_1}}$ と，$\boldsymbol{r}_2$ から点 $\boldsymbol{r}_1$ までの曲線 ${\color{blue}{C_2}}$ からなる閉曲線 $C$ を考えると，
\begin{eqnarray}
0 = \oint_{C} (\nabla \varphi)\cdot d\boldsymbol{r} &=&
{\color{red}{\int_{C_1}}} (\nabla \varphi)\cdot d\boldsymbol{r} +
{\color{blue}{\int_{C_2}}} (\nabla \varphi)\cdot d\boldsymbol{r} \\
\therefore\ \ {\color{red}{\int_{C_1}}} (\nabla \varphi)\cdot d\boldsymbol{r} &=&
-{\color{blue}{\int_{C_2}}} (\nabla \varphi)\cdot d\boldsymbol{r} \\
\therefore\ \ {\color{red}{\int_{\boldsymbol{r}_1}^{\boldsymbol{r}_2}}} (\nabla \varphi)\cdot d\boldsymbol{r} &=&
-{\color{blue}{\int_{\boldsymbol{r}_2}^{\boldsymbol{r}_1}}} (\nabla \varphi)\cdot d\boldsymbol{r} \\
\therefore \ \
\therefore\ \ {\color{red}{\int_{\boldsymbol{r}_1}^{\boldsymbol{r}_2}}} (\nabla \varphi)\cdot d\boldsymbol{r} &=&
{\color{blue}{\int_{\boldsymbol{r}_1}^{\boldsymbol{r}_2}}} (\nabla \varphi)\cdot d\boldsymbol{r}
\end{eqnarray}
このことは，$\boldsymbol{r}_1$ から $\boldsymbol{r}_2$ までの線積分の値が曲線 ${\color{red}{C_1}}$ に沿って計算しても，曲線 ${\color{blue}{C_2}}$ に沿って計算しても同じということ，つまり線積分 $\displaystyle \int_{\boldsymbol{r}_1}^{\boldsymbol{r}_2} (\nabla \varphi)\cdot d\boldsymbol{r}$ は $\boldsymbol{r}_1$ から $\boldsymbol{r}_2$ までの経路の取り方に依存しないということを表す。