ベクトルの足し算,引き算,内積,外積,三重積。
- ベクトル同士の足し算,引き算は,成分同士の足し算,引き算。
$$\boldsymbol{a} \pm \boldsymbol{b} = (a_x \pm b_x) \boldsymbol{i} +(a_y \pm b_y) \boldsymbol{j}+(a_z \pm b_z) \boldsymbol{k}$$ - ベクトルの定数倍は,全成分を定数倍。
$$ k\, \boldsymbol{a} = k\, a_x\, \boldsymbol{i} + k\, a_y\, \boldsymbol{j} + k\, a_z\, \boldsymbol{k} $$ - ベクトルの「割り算」(ベクトルで「割る」こと)は定義されない。
- 掛け算については,2種類,内積(スカラー積)と外積(ベクトル積)。それぞれ,\(\cdot\) と \(\times\) という別の記号で表す。
ベクトルの内積
ベクトルの内積とは2つのベクトルからスカラーを作る演算であり,\(\cdot\) で表す。
基本ベクトル同士の内積の定義
デカルト座標系の基本ベクトル同士の内積を次のように定義する。
$${\color{blue}\boldsymbol{i}\cdot\boldsymbol{i}} = {\color{blue}\boldsymbol{j}\cdot\boldsymbol{j}} = {\color{blue}\boldsymbol{k}\cdot\boldsymbol{k}} =1$$$$ \boldsymbol{i}\cdot\boldsymbol{j} =\boldsymbol{j}\cdot\boldsymbol{i} = 0$$$$\boldsymbol{j}\cdot\boldsymbol{k} =\boldsymbol{k}\cdot\boldsymbol{j} = 0$$$$\boldsymbol{k}\cdot\boldsymbol{i} =\boldsymbol{i}\cdot\boldsymbol{k} = 0$$
自分自身との内積は \(1\)。自分自身以外との内積は \(0\)。
一般のベクトル同士の内積は…
$$\boldsymbol{a} = a_x \, \boldsymbol{i} + a_y \, \boldsymbol{j} +a_z \, \boldsymbol{k}$$ $$\boldsymbol{b} = b_x \, \boldsymbol{i} + b_y \, \boldsymbol{j} +b_z \, \boldsymbol{k}$$ とすると,基本ベクトル同士の内積の定義から(内積について分配則が成り立つことを前提として)以下のような結果が導かれる。
\begin{eqnarray}
\boldsymbol{a}\cdot\boldsymbol{b} &=& \left( a_x \, \boldsymbol{i} + a_y \, \boldsymbol{j} +a_z \, \boldsymbol{k} \right) \cdot \left( b_x \, \boldsymbol{i} + b_y \, \boldsymbol{j} +b_z \, \boldsymbol{k}\right) \\
&=& {\color{white}{ + }\ \ } a_x b_x\, {\color{blue}\boldsymbol{i} \cdot \boldsymbol{i}} +
a_x b_y\, \boldsymbol{i} \cdot \boldsymbol{j} +
a_x b_z\, \boldsymbol{i} \cdot \boldsymbol{k} \\
&& + a_y b_x\, \boldsymbol{j} \cdot \boldsymbol{i} +
a_y b_y\, {\color{blue}\boldsymbol{j} \cdot \boldsymbol{j}} +
a_y b_z\, \boldsymbol{j} \cdot \boldsymbol{k} \\
&& + a_z b_x\, \boldsymbol{k} \cdot \boldsymbol{i} +
a_z b_y\, \boldsymbol{k} \cdot \boldsymbol{j} +
a_z b_z\, {\color{blue}\boldsymbol{k} \cdot \boldsymbol{k}} \\
&=& a_x b_x + a_y b_y + a_z b_z
\end{eqnarray}
すなわち
$$\boldsymbol{a}\cdot\boldsymbol{b} = a_x b_x + a_y b_y + a_z b_z$$
以後はこれを一般のベクトル同士の内積の定義にする。
ベクトルの内積について
- 内積記号省略不可! \( \boldsymbol{a}\cdot \boldsymbol{b} \) を \( \boldsymbol{a}\ \boldsymbol{b} \) なんて書いたらダメ!
- 交換則が成り立つ: \(\boldsymbol{a}\cdot\boldsymbol{b} = \boldsymbol{b}\cdot\boldsymbol{a} \)
- 分配則が成り立つ: \(\boldsymbol{a}\cdot (\boldsymbol{b} + \boldsymbol{c}) = \boldsymbol{a}\cdot\boldsymbol{b} + \boldsymbol{a}\cdot\boldsymbol{c}\), etc.
ベクトルの大きさ
$$ |\boldsymbol{a} | \equiv \sqrt{\boldsymbol{a}\cdot\boldsymbol{a}} = \sqrt{a_x^2 + a_y^2 + a_z^2} $$
内積のもう一つの表し方
$$\boldsymbol{a}\cdot\boldsymbol{b} = |\boldsymbol{a} | |\boldsymbol{b} | \cos\theta$$ ここで \(\theta \) は2つのベクトルのなす角。
教科書によっては(ほとんどのテキストでは),\(\boldsymbol{a}\cdot\boldsymbol{b} \equiv |\boldsymbol{a} | |\boldsymbol{b} | \cos\theta\) を内積の「定義」としているものもあるが,ここではこれを第1義的な定義としては採用しない。なぜなら,この定義の右辺に現れるベクトルの大きさ \( |\boldsymbol{a} |\) は,自分自身との内積の平方根として定義されるはずであり,ベクトルの大きさを使う前に内積を定義しておくことが必要かなと考えるからである。
この式については,もう一つの定義として頭ごなしに覚えるというよりも,最初に導いた定義:
$$\boldsymbol{a}\cdot\boldsymbol{b} = a_x b_x + a_y b_y + a_z b_z$$ から導かれることを示すことができる。
説明の概要は以下の通り:
簡単のために,\( \boldsymbol{a}, \boldsymbol{b} \) は \(xy\) 平面上にあるとし,さらに \( \boldsymbol{a} \) は\(x\) 軸上,\(+x\) の向きにあるとする。すると,
\begin{eqnarray}
\boldsymbol{a} &=& (a_x, a_y, a_z) = (|\boldsymbol{a}|, 0, 0) \\
\boldsymbol{b} &=& (b_x, b_y, b_z) = (|\boldsymbol{b}| \cos\theta, |\boldsymbol{b}| \sin\theta, 0) \end{eqnarray}
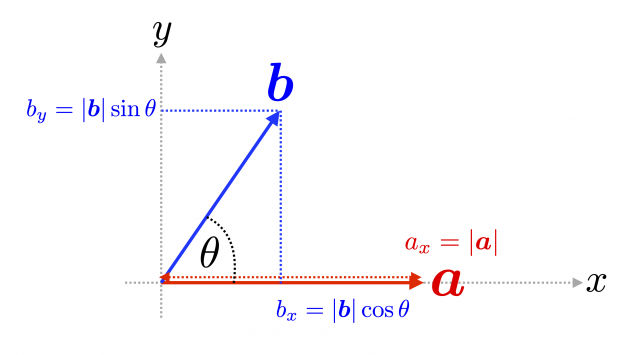
内積の定義から
\begin{eqnarray}
\boldsymbol{a}\cdot\boldsymbol{b} &=& a_x b_x + a_y b_y + a_z b_z \\
&=& a_x b_x + 0 + 0\\
&=& |\boldsymbol{a}|\, |\boldsymbol{b}| \cos\theta
\end{eqnarray} いったん証明されると,この式は座標系の取り方によらずに成り立つので,\( \boldsymbol{a}, \boldsymbol{b} \) が \(xy\) 平面上にないような一般の場合にも成り立つ。
この表し方からすぐにわかること:ゼロ・ベクトルでない2つのベクトル \(\boldsymbol{a}, \, \boldsymbol{b} \) の内積がゼロであれば,2つのベクトルは直交する。
$$\boldsymbol{a}\cdot\boldsymbol{b} = 0 \quad\Leftrightarrow \quad \cos\theta = 0 \quad\Leftrightarrow\quad \theta = \frac{\pi}{2}, \ \ \mbox{i.e.,}\ \ \boldsymbol{a}\perp\boldsymbol{b}$$
あらためて基本ベクトル同士の内積の定義を解釈する
さて,2つのベクトルの内積が
$$\boldsymbol{a}\cdot\boldsymbol{b} = |\boldsymbol{a} | |\boldsymbol{b} | \cos\theta$$
ここで \(\theta \) は2つのベクトルのなす角,特に自分自身との内積は
$$\boldsymbol{a}\cdot\boldsymbol{a} = |\boldsymbol{a} |^2$$
となることがわかったので,あらためて,基本ベクトルの内積の定義を解釈してみる。
$$\boldsymbol{i}\cdot\boldsymbol{i} = \boldsymbol{j}\cdot\boldsymbol{j} = \boldsymbol{k}\cdot\boldsymbol{k} =1$$
ということは,基本ベクトルの大きさが $1$ であることを示す。また,
$$ \boldsymbol{i}\cdot\boldsymbol{j} =\boldsymbol{j}\cdot\boldsymbol{i} = 0$$$$\boldsymbol{j}\cdot\boldsymbol{k} =\boldsymbol{k}\cdot\boldsymbol{j} = 0$$$$\boldsymbol{k}\cdot\boldsymbol{i} =\boldsymbol{i}\cdot\boldsymbol{k} = 0$$
は基本ベクトル $\boldsymbol{i}, \, \boldsymbol{j}, \, \boldsymbol{k}$ は互いに直交していることを示している。
このように,大きさが $1$ で互いに直交している基本ベクトルのことを正規直交基底などと言ったりする。
ベクトルの外積
3次元ベクトル同士のもうひとつの掛け算。外積とは,2つのベクトルから別のベクトルをつくる演算。外積の記号は $\times $。掛け算と同じ記号だが,省略不可! 答えがベクトルになることに注意。
基本ベクトル同士の外積の定義
\begin{eqnarray}
{\color{blue}\boldsymbol{i}\times \boldsymbol{j}} &=& \boldsymbol{k} \\
{\color{blue}\boldsymbol{j}\times \boldsymbol{k}} &=& \boldsymbol{i} \\
{\color{blue}\boldsymbol{k}\times \boldsymbol{i}} &=& \boldsymbol{j}
\end{eqnarray}
サイクリック(循環的)であることに注意。また,
\begin{eqnarray}
{\color{green}\boldsymbol{j}\times \boldsymbol{i}} &=& -{\color{blue}\boldsymbol{i}\times \boldsymbol{j}} = -\boldsymbol{k} \\
{\color{green}\boldsymbol{k}\times \boldsymbol{j}} &=& -{\color{blue}\boldsymbol{j}\times \boldsymbol{k}} = -\boldsymbol{i} \\
{\color{green}\boldsymbol{i}\times \boldsymbol{k}} &=& -{\color{blue}\boldsymbol{k}\times \boldsymbol{i}} = -\boldsymbol{j}
\end{eqnarray}
順序を変えると負号がつくことに注意。最後に,
$$ \boldsymbol{i} \times \boldsymbol{i} = \boldsymbol{j} \times \boldsymbol{j} = \boldsymbol{k} \times \boldsymbol{k} = \boldsymbol{0}$$
自分自身との外積はゼロ・ベクトル。
一般のベクトル同士の外積は…
$$\boldsymbol{a} = a_x \, \boldsymbol{i} + a_y \, \boldsymbol{j} +a_z \, \boldsymbol{k}$$
$$\boldsymbol{b} = b_x \, \boldsymbol{i} + b_y \, \boldsymbol{j} +b_z \, \boldsymbol{k}$$
とすると,基本ベクトル同士の外積の定義から(外積について分配則が成り立つことを前提として)以下のような結果が導かれる。
\begin{eqnarray}
\boldsymbol{a}\times\boldsymbol{b} &=& \left( a_x \, \boldsymbol{i} + a_y \, \boldsymbol{j} +a_z \, \boldsymbol{k} \right) \times \left( b_x \, \boldsymbol{i} + b_y \, \boldsymbol{j} +b_z \, \boldsymbol{k}\right) \\
&=&{\color{white}{+}\ \ }{\color{gray}{a_x b_x\, \boldsymbol{i} \times \boldsymbol{i} }}+
a_x b_y\, {\color{blue}\boldsymbol{i} \times \boldsymbol{j} }+
a_x b_z\, {\color{green}\boldsymbol{i} \times \boldsymbol{k} }\\
&& + a_y b_x\, {\color{green}\boldsymbol{j} \times \boldsymbol{i} }+
{\color{gray}{a_y b_y\, \boldsymbol{j} \times \boldsymbol{j} }}+
a_y b_z\, {\color{blue}\boldsymbol{j} \times \boldsymbol{k}} \\
&& + a_z b_x\, {\color{blue}\boldsymbol{k} \times \boldsymbol{i}} +
a_z b_y\, {\color{green}\boldsymbol{k} \times \boldsymbol{j}} +
{\color{gray}{a_z b_z\, \boldsymbol{k} \times \boldsymbol{k} }}\\
&=& {\color{white}{+}\ \ }
a_x b_y\, {\color{blue}\boldsymbol{i} \times \boldsymbol{j} }
\, -\, a_x b_z\, {\color{blue}\boldsymbol{k} \times \boldsymbol{i}} \\
&& \, -\, a_y b_x\, {\color{blue}\boldsymbol{i} \times \boldsymbol{j}}
+
a_y b_z\, {\color{blue}\boldsymbol{j} \times \boldsymbol{k}} \\
&& + a_z b_x\, {\color{blue}\boldsymbol{k} \times \boldsymbol{i} }
-a_z b_y\, {\color{blue}\boldsymbol{j} \times \boldsymbol{k} }
\\
&=& (a_y b_z -a_z b_y) \,\boldsymbol{i} + (a_z b_x -a_x b_z) \,\boldsymbol{j} +(a_x b_y -a_y b_x) \,\boldsymbol{k}
\end{eqnarray}
すなわち
$$\boldsymbol{a}\times\boldsymbol{b} = (a_y b_z -a_z b_y) \,\boldsymbol{i} + (a_z b_x -a_x b_z) \,\boldsymbol{j} +(a_x b_y -a_y b_x) \,\boldsymbol{k} $$ 以後はこれを外積の定義として,これを使って計算する。
ベクトルの外積については,交換則が成り立たない
\begin{eqnarray}
\boldsymbol{b} \times \boldsymbol{a} &=& {\color{white}{+}\ \ }
(b_y a_z -b_z a_y) \,\boldsymbol{i} +(b_z a_x -b_x a_z) \,\boldsymbol{j} + (b_x a_y -b_y a_x) \,\boldsymbol{k} \\
&=& -(a_y b_z -a_z b_y) \,\boldsymbol{i} -(a_z b_x -a_x b_z) \,\boldsymbol{j} -(a_x b_y -a_y b_x) \,\boldsymbol{k} \\
&=& -\boldsymbol{a} \times \boldsymbol{b}
\end{eqnarray}
つまり,$$\boldsymbol{b} \times \boldsymbol{a} = -\boldsymbol{a} \times \boldsymbol{b}$$ 順序を交換するとマイナスがつくということで「反交換」であるという言い方もある。
外積の反交換性からすぐに導かれることがある。それは,自分自身との外積はゼロ・ベクトルであること。証明は簡単で,反交換であることから
$$ {\color{blue}\boldsymbol{a}} \times\boldsymbol{a} = -\boldsymbol{a} \times {\color{blue}\boldsymbol{a}}$$
左辺に移行して
$$ 2 \,\boldsymbol{a} \times\boldsymbol{a} = \boldsymbol{0} \quad\therefore \boldsymbol{a} \times\boldsymbol{a} = \boldsymbol{0} $$
ベクトルの外積について
- 外積記号省略不可! \(\boldsymbol{a}\times\boldsymbol{b}\) を \(\boldsymbol{a}\,\boldsymbol{b}\) なんて省略して書いたらダメ!
- 交換則は成り立たない: \( \boldsymbol{a} \times \boldsymbol{b} \neq \boldsymbol{b} \times \boldsymbol{a}\) むしろ反交換である:\( \boldsymbol{a} \times \boldsymbol{b} = -\boldsymbol{b} \times \boldsymbol{a}\)
- 分配則が成り立つ: \(\boldsymbol{a}\times\left( \boldsymbol{b} + \boldsymbol{c}\right) = \boldsymbol{a}\times\boldsymbol{b} + \boldsymbol{a}\times\boldsymbol{c}\), etc.
外積のもう一つの表し方
$$\boldsymbol{a} \times \boldsymbol{b} = |\boldsymbol{a}| |\boldsymbol{b}| \sin\theta \ \boldsymbol{n}$$ ここで \(\theta\) は2つのベクトル \(\boldsymbol{a}, \, \boldsymbol{b} \) のなす角であり,\(\boldsymbol{n}\) は \(\boldsymbol{a}\) にも \(\boldsymbol{b}\) にも直交し,向きが \(\boldsymbol{a}\) から \(\boldsymbol{b}\) に右ねじを回したときの進行方向であるような単位ベクトル。
この表し方も,上に述べたベクトルの外積の定義から求められることを示す。
説明の概要は以下の通り:
簡単のために,\( \boldsymbol{a}, \boldsymbol{b} \) は \(xy\) 平面上にあるとし,さらに \( \boldsymbol{a} \) は\(x\) 軸上,\(+x\) の向きにあるとする。すると,
\begin{eqnarray}
\boldsymbol{a} &=& (a_x, a_y, a_z) = (|\boldsymbol{a}|, 0, 0) \\
\boldsymbol{b} &=& (b_x, b_y, b_z) = (|\boldsymbol{b}| \cos\theta, |\boldsymbol{b}| \sin\theta, 0) \end{eqnarray} 外積の定義から
\begin{eqnarray} \left(\boldsymbol{a}\times\boldsymbol{b} \right)_x &=& a_y b_z -a_z b_y = 0 \\
\left(\boldsymbol{a}\times\boldsymbol{b} \right)_y &=& a_z b_x -a_x b_z = 0 \\
\left(\boldsymbol{a}\times\boldsymbol{b} \right)_z &=& a_x b_y -a_y b_x = |\boldsymbol{a}|\,|\boldsymbol{b}| \sin\theta \\
\therefore \boldsymbol{a}\times\boldsymbol{b} &=& |\boldsymbol{a}|\,|\boldsymbol{b}| \sin\theta \,\boldsymbol{k}
\equiv
|\boldsymbol{a}|\,|\boldsymbol{b}| \sin\theta \,\boldsymbol{n}
\end{eqnarray}
(ここでは \(\boldsymbol{n}\) すなわち \(\boldsymbol{k}\) が \(\boldsymbol{a}\) にも \(\boldsymbol{b}\) にも直交する単位ベクトル。)いったん証明されると,この式は座標系の取り方によらずに成り立つので,\( \boldsymbol{a}, \boldsymbol{b} \) が \(xy\) 平面上にないような一般の場合にも成り立つ。
\(| \boldsymbol{a} \times \boldsymbol{b} |\) は2つのベクトル \(\boldsymbol{a}, \, \boldsymbol{b} \) で作られる平行四辺形の面積を表すことは以下の図からわかる。
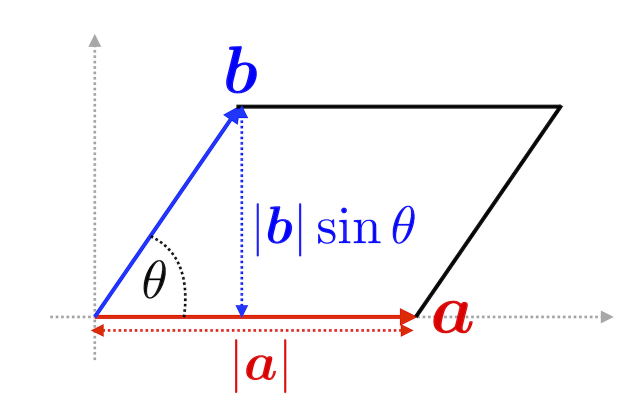
また,自分自身との外積はゼロベクトルであることはすでに述べたが,2つのベクトルが平行であれば,外積はゼロベクトルである。証明は以下の通り。
\(\boldsymbol{b}\) が \(\boldsymbol{a}\) に平行であるということは,ある定数 \(k\) を使って,\(\boldsymbol{b}= k \boldsymbol{a}\) と書けるということ。したがって,
$$\boldsymbol{a}\times\boldsymbol{b} = \boldsymbol{a}\times(k \boldsymbol{a} ) = k \boldsymbol{a}\times\boldsymbol{a} =\boldsymbol{0}$$
ベクトルの三重積
3つのベクトルによる「掛け算」
スカラー三重積
3つのベクトルの「掛け算」によって最終的にスカラーをつくる演算なので,ベクトルの「スカラー三重積」と呼ぶ(まぎらわしい)。
$$\boldsymbol{a}\cdot (\boldsymbol{b} \times \boldsymbol{c})$$ これがスカラーをつくるということは,以下のようにしてわかる。
- 先にかっこで囲まれた部分を計算するので \( (\boldsymbol{b} \times \boldsymbol{c}) \) は外積なのでベクトルを作る。これをたとえば \(\boldsymbol{d}\) としよう。$$\boldsymbol{b} \times \boldsymbol{c} = \boldsymbol{d}$$
- 次に,\(\boldsymbol{a}\cdot\boldsymbol{d}\) を計算するが,これは内積なので最終的に答えはスカラー。
スカラー三重積の重要な公式
$$ \boldsymbol{a}\cdot (\boldsymbol{b} \times \boldsymbol{c}) = \boldsymbol{b}\cdot (\boldsymbol{c} \times \boldsymbol{a}) = \boldsymbol{c}\cdot (\boldsymbol{a} \times \boldsymbol{b}) $$
\boldsymbol{a}\cdot (\boldsymbol{b} \times \boldsymbol{c}) &=&
a_x (\boldsymbol{b} \times \boldsymbol{c})_x + a_y (\boldsymbol{b} \times \boldsymbol{c})_y + a_z (\boldsymbol{b} \times \boldsymbol{c})_z \\
&=& a_x ({\color{blue}{b_y}} c_z -{\color{green}{b_z}} c_y) + a_y ({\color{green}{b_z}} c_x -{\color{red}{b_x}} c_z) + a_z ({\color{red}{b_x}} c_y -{\color{blue}{b_y}} c_x) \\
&=& {\color{red}{b_x}} (c_y a_z -c_z a_y) + {\color{blue}{b_y}} (c_z a_x -c_x a_z) + {\color{green}{b_z}} (c_x a_y -c_y a_x) \\
&=& b_x (\boldsymbol{c}\times\boldsymbol{a})_x + b_y (\boldsymbol{c}\times\boldsymbol{a})_y + b_z (\boldsymbol{c}\times\boldsymbol{a})_z \\
&=& \boldsymbol{b}\cdot (\boldsymbol{c}\times\boldsymbol{a})
\end{eqnarray}
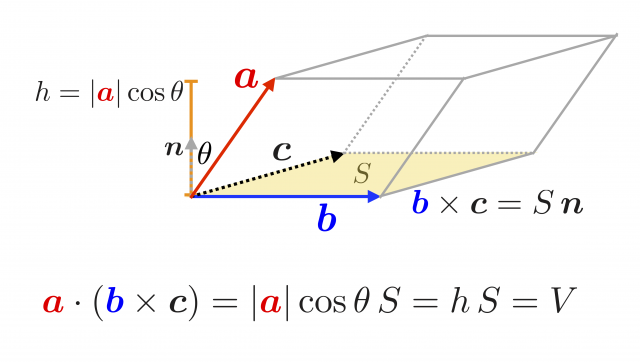
参考:
ベクトル三重積
- 先にかっこで囲まれた部分の計算。\( (\boldsymbol{b}\times\boldsymbol{c}) \) は外積なのでベクトルを作る。これをたとえば \(\boldsymbol{d}\) としよう。
- 次に,\( \boldsymbol{a}\times\boldsymbol{d} \) を計算するが,これは外積なので最終的に答えはベクトル。
外積の「結合則」は成り立たない。つまり,$$\boldsymbol{a} \times (\boldsymbol{b}\times\boldsymbol{c}) {\color{red}{\neq}} (\boldsymbol{a}\times\boldsymbol{b}) \times \boldsymbol{c}$$
ベクトル三重積の重要な公式
$$\boldsymbol{a} \times (\boldsymbol{b}\times\boldsymbol{c}) = (\boldsymbol{a}\cdot\boldsymbol{c}) \boldsymbol{b} -(\boldsymbol{a}\cdot\boldsymbol{b}) \boldsymbol{c} $$
成分を直接計算してこの公式が成り立つことを示すことができる。
例として $x$ 成分の計算:
\begin{eqnarray}
\bigl\{\boldsymbol{a}\times(\boldsymbol{b}\times\boldsymbol{c})\bigr\}_x &=& a_y (\boldsymbol{b}\times\boldsymbol{c})_z -a_z (\boldsymbol{b}\times\boldsymbol{c})_y \\
&=& a_y ({\color{blue}{b_x}} c_y -b_y {\color{green}{c_x}}) -a_z (b_z {\color{green}{c_x}} -{\color{blue}{b_x}} c_z) \\
&=& ({\color{white}{a_x c_x}} {\color{white}{+}\ \, } a_y c_y + a_z c_z) {\color{blue}{b_x}} -({\color{white}{a_x b_x}\ }{\color{white}{+}} a_y b_y + a_z b_x) {\color{green}{c_x}} \\
&=& (a_x c_x + a_y c_y + a_z c_z) {\color{blue}{b_x} } -(a_x b_x + a_y b_y + a_z b_x) {\color{green}{c_x}} \\
&=& \bigl\{(\boldsymbol{a}\cdot\boldsymbol{c}) \boldsymbol{b} -(\boldsymbol{a}\cdot\boldsymbol{b}) \boldsymbol{c} \bigr\}_x
\end{eqnarray}
ベクトルの演算のまとめ
以上の結果をまとめると…
ベクトルの表し方
$$ \boldsymbol{a} = a_x \,\boldsymbol{i} + a_y \,\boldsymbol{j} + a_z \,\boldsymbol{k}$$ または $$ \boldsymbol{a} = (a_x, \ a_y, \ a_z) $$
ベクトルの内積
$$\boldsymbol{a}\cdot\boldsymbol{b} = a_x b_x + a_y b_y + a_z b_z = |\boldsymbol{a} | |\boldsymbol{b} | \cos\theta$$
ベクトルの大きさ
$$ |\boldsymbol{a} | \equiv \sqrt{\boldsymbol{a}\cdot\boldsymbol{a}} = \sqrt{a_x^2 + a_y^2 + a_z^2} $$
ベクトルの外積
\begin{eqnarray}
\boldsymbol{a}\times\boldsymbol{b} &=& (a_y b_z -a_z b_y) \,\boldsymbol{i} + (a_z b_x -a_x b_z) \,\boldsymbol{j} +(a_x b_y -a_y b_x) \,\boldsymbol{k} \\
&=& |\boldsymbol{a}| |\boldsymbol{b}| \sin\theta\ \boldsymbol{n}
\end{eqnarray}
\(\boldsymbol{n}\) は \(\boldsymbol{a}\) にも \(\boldsymbol{b}\) にも直交し,向きが \(\boldsymbol{a}\) から \(\boldsymbol{b}\) に右ねじを回したときの進行方向であるような単位ベクトル。
スカラー三重積の公式
$$ \boldsymbol{a}\cdot (\boldsymbol{b} \times \boldsymbol{c}) = \boldsymbol{b}\cdot (\boldsymbol{c} \times \boldsymbol{a}) = \boldsymbol{c}\cdot (\boldsymbol{a} \times \boldsymbol{b}) $$
ベクトル三重積の公式
$$\boldsymbol{a} \times (\boldsymbol{b}\times\boldsymbol{c}) = (\boldsymbol{a}\cdot\boldsymbol{c}) \boldsymbol{b} -(\boldsymbol{a}\cdot\boldsymbol{b}) \boldsymbol{c} $$