3次元ベクトルの表し方
3次元ベクトルの表し方についてまとめる。
- デカルト座標系（\(xyz\)- 系）の基本ベクトル \(\boldsymbol{i}, \,\boldsymbol{j},\, \boldsymbol{k}\) と成分 \( a_x, \,a_y, \,a_z \) を使って，$$ \boldsymbol{a} = a_x \,\boldsymbol{i} + a_y \,\boldsymbol{j} + a_z \,\boldsymbol{k}$$
この書き方が最も正式な表記法。
特に，全ての成分がゼロであるベクトルを「ゼロベクトル」と呼び，以下のようにベクトルらしく「数式フォントの太字」で \(\boldsymbol{0}\) と書く。
$$\boldsymbol{0} = 0\, \boldsymbol{i} + 0\, \boldsymbol{j} + 0\, \boldsymbol{k}$$ - 線形代数学では，ベクトルと言えば「列ベクトル」（成分を縦にならべたもの）のこと。
$$\boldsymbol{a} = \left(
\begin{array}{c}
a_x \\
a_y \\
a_z
\end{array}
\right)$$
列ベクトルの転置をとった行ベクトル $ \boldsymbol{a}^T = (a_x\ \ a_y\ \ a_z) $ もあるが，成分の間はスペースで区切る。
さらに言えば，\(xyz\)-系でなくてもよく，成分の数も3つだけである必要もないので $n$ 次元ベクトルの成分表示は，
$$\boldsymbol{a} = \left(
\begin{array}{c}
a_1 \\
a_2 \\
\vdots \\
a_n
\end{array}
\right)$$ - 力学，電磁気学等では，いちいち基本ベクトルを書かずに
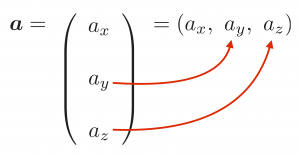
$$ \boldsymbol{a} = (a_x, \ a_y, \ a_z) $$ と成分の間をカンマ $,$ で区切って横に並べる。
ベクトルの成分表記，カンマで区切る？区切らない？
$$ \boldsymbol{a} = (a_x, \ a_y, \ a_z) $$ と表記する場合と，
$$\boldsymbol{a} = \left(
\begin{array}{c}
a_x \\
a_y \\
a_z
\end{array}
\right)$$
または
$$ \boldsymbol{a}^T = (a_x\ \ a_y\ \ a_z) $$
カンマで区切ればいいの？区切らなくてもいいの？どっち？？ … と悩む人のために。
あくまでも正式な成分表記法は，「列ベクトル」（成分を縦にならべたもの）であり，
$$\boldsymbol{a} = \left(
\begin{array}{c}
a_x \\
a_y \\
a_z
\end{array}
\right)$$
でも，これだとスペースを消費するので，
$$ \boldsymbol{a} = (a_x, \ a_y, \ a_z) $$
と書いて，$a_x$ のあとのカンマ$, $ は実は改行して次の行を表すんだ，と理解する。また $a_y$ のあとのカンマ $, $ も実はさらに改行して次の行を表すんだと理解すれば，$\boldsymbol{a} = (a_x, \ a_y, \ a_z) $ は結局3行にわたる成分表記を1行にまとめて節約表示する方法である，ということになる。
このように思えば，成分の間をスペースのみにするか，カンマで区切るか，という異なった表記法と折り合いをつけて生きていくことができると思うが，いかがでしょうか？
