ガウスの定理
$$ \iiint_V \nabla\cdot \boldsymbol{a}\ dV = \iint_S \boldsymbol{a}\cdot\boldsymbol{n}\ dS$$
ここで,\(S\) は体積 \(V\) の立体を囲む閉曲面,\(dS\) はその表面の微小面積部分,\(\boldsymbol{n}\) は微小面積 \(dS\) に垂直な単位ベクトル(向きは立体の外側を向く)。
右辺が閉曲面 $S$ 上での面積分であることを強調するために,右辺を以下のように書くべきだというのが私の意見。
$$\iiint_V \nabla\cdot \boldsymbol{a}\, dV = {\color{red}\int\!\!\!\!\!\!\bigcirc\!\!\!\!\!\!\int}_{\!\!S} \ \boldsymbol{a}\cdot\boldsymbol{n} \ dS$$(でも $\color{red}\displaystyle\int\!\!\!\!\!\!\bigcirc\!\!\!\!\!\!\int$ を書くのは大変なんだよなぁ,Mathjax では \userpackage{esint} が使えないようで,$\oiint$ や $\varoiint$ が効かない。)
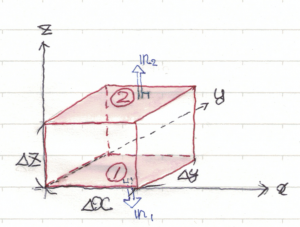
図のように,それぞれの辺の長さが \(\varDelta x, \varDelta y, \varDelta z\) である微小直方体を考え,この体積を囲む面からのベクトル \(\boldsymbol{a}\) の流束( \(\boldsymbol{a}\) の面に垂直な成分の面積分,微小面積の場合は単に「垂直成分」かける「面積」)を計算する。
まず,面②から出る流束は $$(\boldsymbol{a}\cdot\boldsymbol{n})_2\, \varDelta S_2 = a_z(\varDelta z) \varDelta x\, \varDelta y = \left\{a_z(0) + \frac{\partial a_z}{\partial z} \varDelta z \right\} \varDelta x \,\varDelta y$$
同様にして,面①から出る流束は $$(\boldsymbol{a}\cdot\boldsymbol{n})_1\, \varDelta S_1 = -a_z(0) \,\varDelta x\, \varDelta y $$ ここでマイナスがつくのは,\(\boldsymbol{n}\) が立体の表面外向きのベクトルであるから。
\(z\) 軸に直交するこの二つの面の流束を足すと,$z$ 方向の正味の流速 $(\boldsymbol{a}\cdot\boldsymbol{n})_z\, \varDelta S_z$ は
\begin{eqnarray}
(\boldsymbol{a}\cdot\boldsymbol{n})_z\, \varDelta S_z &=& (\boldsymbol{a}\cdot\boldsymbol{n})_1\, \varDelta S_1 + (\boldsymbol{a}\cdot\boldsymbol{n})_2\, \varDelta S_2 \\
&=& \frac{\partial a_z}{\partial z}\ \varDelta x\, \varDelta y\, \varDelta z
\end{eqnarray}
ここで $z$ 軸に垂直な微小面積として $\varDelta S_z \equiv \varDelta x\, \varDelta y$ と定義した。
$x$ 方向,$y$ 方向,$z$ 方向の6面全部を考えると,この微小直方体から出る流束の和は,
\begin{eqnarray}
(\boldsymbol{a}\cdot\boldsymbol{n}) \,\varDelta S
&=&
(\boldsymbol{a}\cdot\boldsymbol{n})_x \,\varDelta S_x
+ (\boldsymbol{a}\cdot\boldsymbol{n})_y \,\varDelta S_y
+ (\boldsymbol{a}\cdot\boldsymbol{n})_z \,\varDelta S_z \\
&=& \left( \frac{\partial a_x}{\partial x} + \frac{\partial a_y}{\partial y} + \frac{\partial a_z}{\partial z} \right) \ \varDelta x\, \varDelta y\, \varDelta z \\
&=& \nabla\cdot\boldsymbol{a} \ \varDelta V \\ \ \\
\therefore\ \ (\boldsymbol{a}\cdot\boldsymbol{n}) \,\varDelta S &=& \nabla\cdot\boldsymbol{a} \ \varDelta V
\end{eqnarray}
これが,微小直方体 $\varDelta V$ を囲む微小閉曲面 $\varDelta S$ から出る流速 $(\boldsymbol{a}\cdot\boldsymbol{n}) \,\varDelta S$ と,$\varDelta V$ 内のベクトル $\boldsymbol{a}$ の発散との間の関係である。
有限の体積 \(V\) の立体とそれを囲む表面 \(S\) については,それらを構成している微小要素の総和を取ることになるが,無限小連続極限では $\displaystyle \sum_i\, \varDelta S_i \Rightarrow \iint_S \,dS, \ \sum_i\, \varDelta V_i \Rightarrow \iiint_V \, dV$ となることから
\begin{eqnarray}
\sum_i \left\{(\boldsymbol{a}\cdot\boldsymbol{n}) \,\varDelta S\right\}_i &=& \sum_i \left\{\nabla\cdot\boldsymbol{a} \,\varDelta V\right\}_i \\
&\Downarrow & \\
\iint_S \boldsymbol{a}\cdot\boldsymbol{n}\ dS &=& \iiint_V \nabla\cdot\boldsymbol{a} \ dV
\end{eqnarray}