直線電流による電場
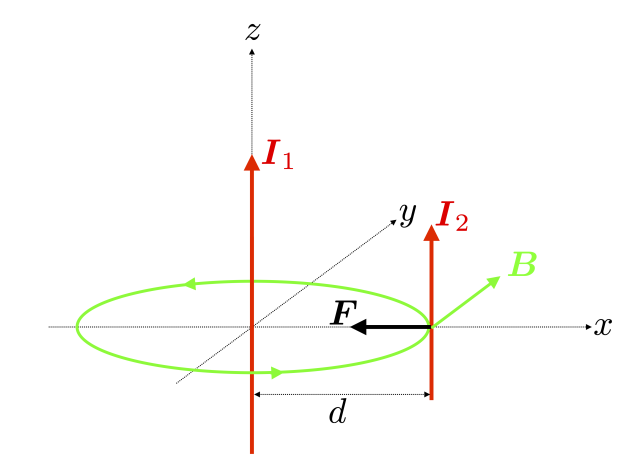
上図のような平行直線電流を考える。
電流 $\boldsymbol{I}_1$ が $\boldsymbol{I}_2$ の位置につくる磁束密度 $\boldsymbol{B}$ は
$$\boldsymbol{B} = \frac{1}{2\pi \varepsilon_0 c^2} \frac{\boldsymbol{I}_1\times\boldsymbol{\rho}}{\rho^2}= \frac{\mu_0}{2\pi } \frac{\boldsymbol{I}_1\times\boldsymbol{\rho}}{\rho^2}$$
であった。（「直線電流による磁場」を参照。）ここでは，$\boldsymbol{I}_1 = (0, 0, I_1)$， $\boldsymbol{\rho} = (d, 0, 0)$ であるから，
$$\boldsymbol{B} = (0, B, 0) = \left( 0, \frac{\mu_0\,I_1}{2\pi \,d}, 0 \right)$$
電流にはたらく力
電流 $\boldsymbol{I}_2$ にはたらく単位長さあたりの力 $\boldsymbol{f}$ は
$$\boldsymbol{f}\equiv\frac{\varDelta \boldsymbol{F} }{\varDelta L} = \boldsymbol{I}_2 \times \boldsymbol{B}$$
であった（「電流素片にはたらく力 」を参照。）ここでは，$\boldsymbol{I}_2 = (0, 0, I_2)$ であるから
$$\boldsymbol{f} = (-f, 0, 0, ) = \left(- \frac{\mu_0\,I_1\,I_2}{2\pi \,d}, 0, 0\right)$$
となる。平行直線電流は，電流が同じ向きであれば $f$ の大きさの力で引き合い，反対向きであれば反発しあう。
真空の透磁率と SI 基本単位の再定義
2019年の SI 基本単位の再定義までは，「$1\, \mbox{m}$ 離れた平行直線電流に $1\, \mbox{A}$ の電流が流れるとき，$1\,\mbox{m}$ あたりに $2 \times 10^{-7}\, \mbox{N}$ の力がはたらく」，として電流単位のアンペア $\mbox{A}$ が定義されていた。
つまり，
\begin{eqnarray}
\Delta L &=& 1 \,(\mbox{m}) \\
d &=& 1 \,\mbox{(m)} \\
I_1 = I_2 &=& 1\,\mbox{(A)} \\
f &=& \frac{\mu_0\,I_1\,I_2}{2\pi \,d} \\
&=& \frac{\mu_0 \times 1 \,(\mbox{A}^2)}{2\pi \times 1\,(\mbox{m})}
= 2 \times 10^{-7}\, (\mbox{N}/\mbox{m} )\\
\therefore\ \ \mu_0 &=& 4 \pi \times 10^{-7}\,(\mbox{N}/\mbox{A}^2) \\
&=& 4 \pi \times 10^{-7}\,(\mbox{H}/\mbox{m})
\end{eqnarray}
となり，真空の透磁率 $\mu_0$ の値は定義値として（誤差がない） $4 \pi \times 10^{-7}$ であった。
新定義では，電気素量 $e = 1.602176634 \times 10^{−19} \, \mbox{(C)}$ が先に定義され，1 秒間に 1 電気素量が流れたときの電流を $1.602176634 \times 10^{−19}\, \mbox{(A)}$ と定義されることになる。