ローレンツ力（「ろーれんつか」ではなく「ろーれんつりょく」）
電磁場を記述する基本方程式であるマクスウェル方程式は解説した。では，その電磁場中においた粒子は，どのような力を受けて運動するか。
すでに，電場の強さを表すベクトル \(\boldsymbol{E}\) を単位電荷にはたらく力として定義した。
（さらに，磁場の強さを表すベクトル \(\boldsymbol{H}\) を単位磁荷にはたらく力として定義したが，磁気単極子は存在しないので，力学的には \(\boldsymbol{H}\) の出る幕はない。）
電場 \(\boldsymbol{E}\)，磁束密度 \(\boldsymbol{B}\) の電磁場中を速度 \(\boldsymbol{v}\) で運動する電荷 \(q\) の荷電粒子は，次のような力 \(\boldsymbol{F}\) を受ける。
$$\boldsymbol{F} = q \left( \boldsymbol{E} + \boldsymbol{v}\times \boldsymbol{B} \right)$$
（念のため，\( \boldsymbol{v}\times \boldsymbol{B}\) は \(\boldsymbol{v}\) と \( \boldsymbol{B}\) の外積）
これをローレンツ力という。したがって，荷電粒子の運動を考えるときには，使う電磁場は \(\boldsymbol{E}\) と \(\boldsymbol{B}\) だからという理由もあり，電磁場を表す4本のベクトルのうち，電場については \(\boldsymbol{D}\) ではなく \(\boldsymbol{E}\)，磁場については \(\boldsymbol{H}\) ではなく \(\boldsymbol{B}\) を採用し，この2本で記述しようというのが \(\boldsymbol{E}\) – \(\boldsymbol{B}\) 対応の立場である。
静電ポテンシャル・保存力・力学的エネルギー保存
別途説明するように，時間的に変動しない電磁場の場合には，電場は以下のようにスカラー場 $\phi$（これを静電ポテンシャルという）の勾配に負号をつけて表すことができる。
$$ \boldsymbol{E} = – \nabla \phi$$
簡単のために，$\boldsymbol{B} = \boldsymbol{0}$ とすると，静電場中の電荷 $q$ が受ける力は
$$\boldsymbol{F} = q \boldsymbol{E} = – \nabla (q \phi) \equiv – \nabla U$$
このように，力 $\boldsymbol{F}$ がスカラー関数 $U$ の勾配に負号をつけた量で書くことができるとき，この力を「保存力」という。
何が保存されるのかというと，運動エネルギーとポテンシャルエネルギー $U$ の和である力学的全エネルギー $E$ が保存される，つまり運動の間，一定であり続ける。このことは以下のように運動方程式から示される。
まず，
$$m \frac{d^2 \boldsymbol{r}}{dt^2} = \boldsymbol{F} = – \nabla U$$
両辺に $\displaystyle \frac{d\boldsymbol{r}}{dt} \cdot$ （内積）をかけてやって…
\begin{eqnarray}
m \frac{d\boldsymbol{r}}{dt} \cdot \frac{d^2 \boldsymbol{r}}{dt^2} &=& – \nabla U \cdot \frac{d\boldsymbol{r}}{dt} \\
\frac{d}{dt} \left\{\frac{1}{2} m \frac{d\boldsymbol{r}}{dt} \cdot \frac{d\boldsymbol{r}}{dt} + U \right\} &=& 0 \\
\therefore\ \ \frac{1}{2} m \frac{d\boldsymbol{r}}{dt} \cdot \frac{d\boldsymbol{r}}{dt} + U &=& \mbox{const.} \equiv E
\end{eqnarray}
電流素片にはたらく力
今度は簡単のために $\boldsymbol{E} = \boldsymbol{0}$ としよう。1個の荷電粒子にはたらく力は
$$\boldsymbol{F} = q \boldsymbol{v} \times \boldsymbol{B}$$
今，単位体積あたり $n$ 個の荷電粒子が同じ速度 $\boldsymbol{v}$ で運動しているとする。
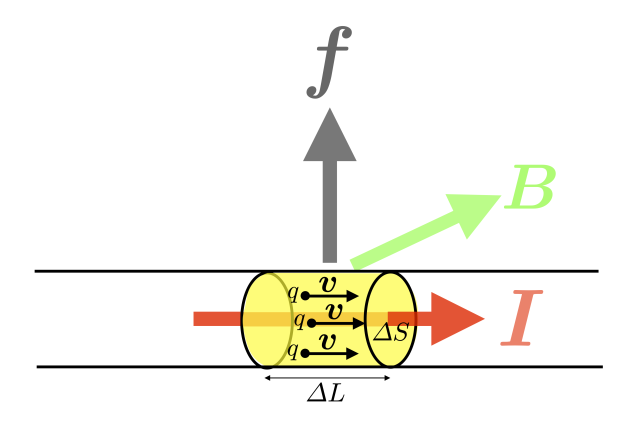$\boldsymbol{v}$ に垂直な微小面積 $\varDelta S$ と $\boldsymbol{v}$ に平行な微小長さ $\varDelta L$ からなる領域を考えると，この素片に働く力 $\varDelta \boldsymbol{F}$ は
\begin{eqnarray}
\varDelta \boldsymbol{F} &=& n \,\varDelta L \,\varDelta S \,q \boldsymbol{v} \times \boldsymbol{B} \\
&=& \varDelta L \,\varDelta S \,\boldsymbol{J} \times \boldsymbol{B} \\
&=& \varDelta L \,\boldsymbol{I} \times \boldsymbol{B}
\end{eqnarray}
ここで，電流密度ベクトルは $\boldsymbol{J} \equiv n q \boldsymbol{v}$ であり，電流ベクトルは $ \boldsymbol{I} \equiv \boldsymbol{J} \varDelta S $ である。
したがって，この電流素片にはたらく単位長さあたりの力 $\boldsymbol{f}$ は
$$\boldsymbol{f}\equiv\frac{\varDelta \boldsymbol{F} }{\varDelta L} = \boldsymbol{I} \times \boldsymbol{B}$$
この式は，後に「平行直線電流にはたらく力」のところで使うことになる。
- 参考：平行直線電流にはたらく力