ストークスの定理
$$ \iint_S (\nabla\times\boldsymbol{a})\cdot\boldsymbol{n}\,dS = \oint_C \boldsymbol{a}\cdot d\boldsymbol{r}$$
ここで \(S\) は閉曲線 \(C\) で囲まれた曲面であり,\(\boldsymbol{n}\) はその曲面の微小面積 \(dS\) に垂直な単位ベクトル。
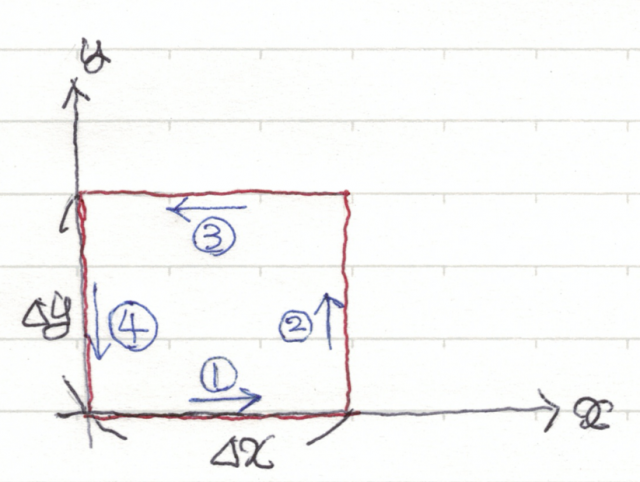
図のように,$z$ 軸に垂直な $xy$ 平面上に,それぞれの辺の長さが \(\varDelta x, \varDelta y\) である微小ループ \(\varDelta C_z\) で囲まれた微小面積 $\varDelta S_z$ を考え,この微小ループに沿ったベクトル \(\boldsymbol{a}\) の接線成分を反時計回りに1周,線積分する。
\begin{eqnarray}
\oint_{\varDelta C_z} \boldsymbol{a}\cdot d\boldsymbol{r} &=& a_x(1) \varDelta x + a_y(2) \varDelta y -a_x(3) \varDelta x -a_y(4) \varDelta y \\
&=& -\left( a_x(3) -a_x(1)\right) \varDelta x + \left(a_y(2) -a_y(4)\right) \varDelta y\\
&=& -\frac{\partial a_x}{\partial y} \varDelta y\, \varDelta x+ \frac{\partial a_y}{\partial x} \varDelta x\, \varDelta y \\
&=& \left(\frac{\partial a_y}{\partial x} -\frac{\partial a_x}{\partial y}\right)\, \varDelta x \varDelta y \\
&=& \left(\nabla\times \boldsymbol{a}\right)_z\, \varDelta x \varDelta y \\
&=& \left(\nabla\times \boldsymbol{a}\right)\cdot\boldsymbol{n}_z \,\varDelta S_z
\end{eqnarray}
この微小ループを積分して,
有限の面積 \(S\) の曲面とそれを囲む閉曲線 \(C\) については,それらを構成している微小要素の総和を取ることになるが,無限小連続極限では $\displaystyle \sum_i \oint_{\varDelta C_i} \Rightarrow \oint_{C}, \ \sum_i\, \varDelta S_i \Rightarrow \iint_S \, dS$ となることから,
\begin{eqnarray}
\sum_i \, \oint_{\varDelta C_i} \boldsymbol{a}\cdot d\boldsymbol{r} &=&
\sum_i \, \left(\nabla\times \boldsymbol{a}\right)\cdot\boldsymbol{n}_i \,\varDelta S_i \\
&\Downarrow & \\
\oint_{C} \boldsymbol{a}\cdot d\boldsymbol{r} &=& \iint_S \left(\nabla\times \boldsymbol{a}\right)\cdot\boldsymbol{n} \,dS
\end{eqnarray}