面積

\(y = f(x) \ (>0), \ y = 0\)(\(x\) 軸)および \(x = a, \ x = b\ (> a)\) で囲まれる部分の面積 \(S\) は
$$S = \int_a^b f(x)\, dx$$ であった。
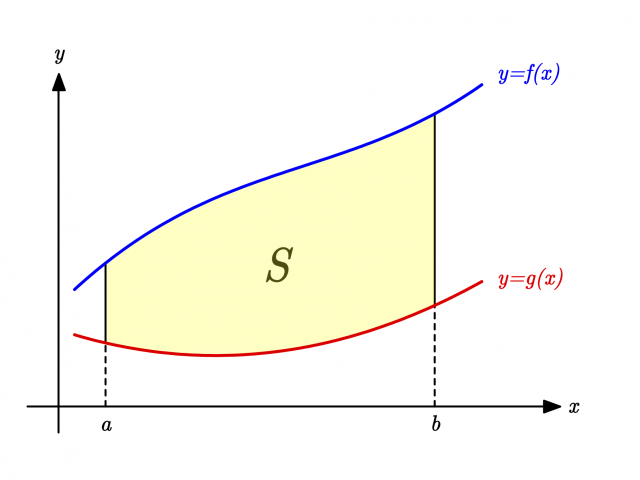
同様に,\(y = f(x), \ y = g(x)\) (\( f(x) > g(x)\) )および \(x = a, \ x = b\ (> a)\) で囲まれる部分の面積は
$$S = \int_a^b \left\{f(x) -g(x)\right\} \, dx$$
曲線の長さ
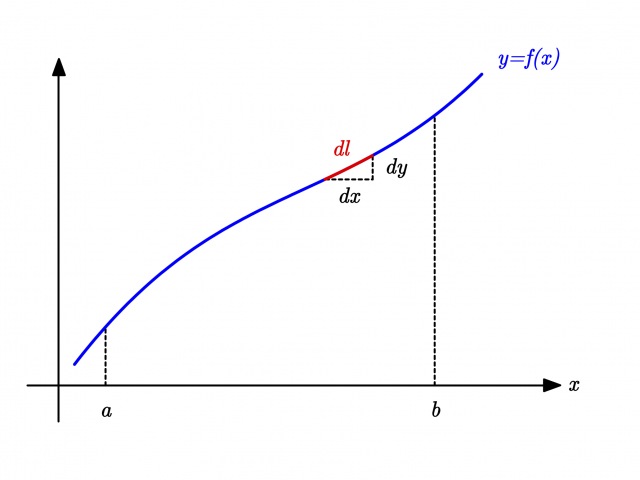
\(y = f(x)\) の \((x, y)\) から \((x+dx, y+dy)\) までの(微小)長さ \(dl \) は
$$dl = \sqrt{dx^2 + dy^2} = \sqrt{1 + \left(\frac{dy}{dx}\right)^2} \,dx$$ であるから,\((a, f(a))\) から \((b, f(b))\) までの曲線の長さは
$$ L = \int_a^b dl =\int_a^b \sqrt{1 + \left(\frac{dy}{dx}\right)^2} \,dx $$
曲線が $x = x(t), \ y = y(t)$ のように媒介変数表示されている場合は,
$$dl = \sqrt{dx^2 + dy^2} = \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} \,dt$$
であるから $(x(t_1), y(t_1))$ から $(x(t_2), y(t_2))$ までの曲線の長さは
$$ L = \int_{t_1}^{t_2} dl =\int_{t_1}^{t_2} \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} \,dt $$
回転体の表面積

関数 \(y = f(x)\) を \(x\) 軸のまわりに回転してできる回転体の側面の面積 \(S\) は,上図のような微小面積 \(dS\) が幅 \(dl\),周長 \(2\pi y\) のリボン状であることから
$$ S = \int_a^b dS = \int_a^b 2\pi y \, dl = \int_a^b 2\pi y \sqrt{1 + \left(\frac{dy}{dx}\right)^2}\,dx$$
回転体の体積
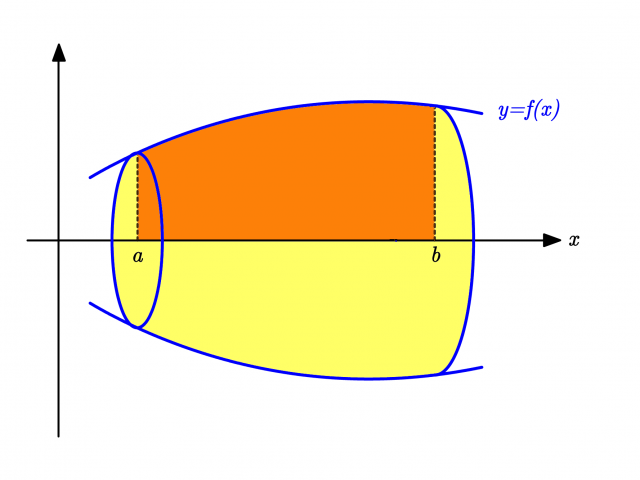
関数 \(y = f(x)\) を \(x\) 軸のまわりに回転してできる回転体の体積 \(V\) は,薄い輪切りにした部分の微小体積 \(dV\) が \(\pi \left\{f(x)\right\}^2 dx\) であることから
$$ V = \int_a^b dV = \int_a^b \pi \left\{f(x)\right\}^2 \,dx$$
例題
円の面積
半径 \(r\) の円の面積。円の方程式 \(x^2 + y^2 = r^2\) より \(y = \pm \sqrt{r^2 -x^2}\)。上半分の面積,つまり \(y = +\sqrt{r^2-x^2}\) と \(x\) 軸で囲まれる部分の面積を求めて2倍すればよいから,
\begin{eqnarray}
S &=& 2 \int_{-r}^r \sqrt{r^2-x^2} \,dx \\
&& \Bigl( x = r\sin t, \ dx = r\cos t\, dt, \ -r \leq x \leq r \ \Rightarrow\ -\frac{\pi}{2} \leq t \leq \frac{\pi}{2} \Bigr)\\
&=& 2 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sqrt{r^2 -r^2 \sin^2 t} \cdot r \cos t\, dt\\
&=& 2r^2 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos^2 t\, dt\\
&=& 2r^2 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1 + \cos 2 t}{2} \, dt\\
&=& r^2 \Bigl[ x + \frac{\sin 2 t}{2} \Bigr]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\\
&=& \pi r^2
\end{eqnarray}
円周
半径 \(r\) の円の円周。円の方程式 \(x^2 + y^2 = r^2\) より \(y = \pm \sqrt{r^2 -x^2}\)。上半分の円周を求めて2倍すればよい。
$$y=\sqrt{r^2 -x^2}, \ \ \frac{dy}{dx} = \frac{1}{2} (r^2 -x^2)^{-\frac{1}{2}}\cdot(-2 x) = -\frac{x}{\sqrt{r^2 -x^2}}$$
$$\sqrt{1+ \left(\frac{dy}{dx}\right)^2} = \sqrt{1 + \frac{x^2}{r^2 -x^2}} = \frac{r}{\sqrt{r^2-x^2}}$$
\begin{eqnarray}
L &=& 2 \int_{-r}^r \sqrt{1+ \left(\frac{dy}{dx}\right)^2}\,x \\
&=& 2\int_{-r}^r \frac{r}{\sqrt{r^2-x^2}}\,x \\
&=& 2 r \int_{-r}^r \frac{1}{\sqrt{1 -\left(\frac{x}{r}\right)^2}} \,\frac{dx}{r} \\
&& \Bigl( \frac{x}{r} = t, \ \frac{dx}{r} = dt, \ -r \leq x \leq r \ \Rightarrow\ -1 \leq t \leq 1\Bigr)\\
&=& 2 r \int_{-1}^1 \frac{1}{\sqrt{1-t^2}} \,dt \\
&=& 2r \Bigl[ \sin^{-1} t \Bigr]_{-1}^1 \\
&=& 2r \left( \frac{\pi}{2} -\left(-\frac{\pi}{2}\right) \right) \\
&=& 2 \pi r
\end{eqnarray}
あるいは,円の方程式 \(x^2 + y^2 = r^2\) が
$$x = r \cos\theta, \quad y = r \sin\theta$$
のように $\theta$ によって媒介変数表示されると思うと
\begin{eqnarray}
L &=& \int_0^{2\pi} \sqrt{\left(\frac{dx}{d\theta}\right)^2 + \left(\frac{dy}{d\theta}\right)^2} \,d\theta\\
&=& \int_0^{2\pi} r \,d\theta \\
&=& 2 \pi \,r
\end{eqnarray}
球の表面積
\( y = \sqrt{r^2 -x^2}\) を\(x\) 軸のまわりに回転してできる半径 \(r\) の球の表面積は
\begin{eqnarray}
S &=& \int_{-r}^r 2\pi y \sqrt{1+ \left(\frac{dy}{dx}\right)^2}\,dx \\
&=& \int_{-r}^r 2\pi \cdot\sqrt{r^2 -x^2}\cdot \frac{r}{\sqrt{r^2-x^2}}\,dx \\
&=&2\pi r\Bigl[ x \Bigr]_{-r}^r\\
&=&4\pi r^2
\end{eqnarray}
球の体積
\( y = \sqrt{r^2 -x^2}\) を\(x\) 軸のまわりに回転してできる半径 \(r\) の球の体積は
\begin{eqnarray}
V &=& \int_{-r}^r \pi y^2 \, dx \\
&=& \int_{-r}^r \pi (r^2 -x^2)\, dx \\
&=& 2 \int_{0}^r \pi (r^2 -x^2)\, dx \\
&=& 2 \pi \Bigl[ r^2 x -\frac{x^3}{3} \Bigr]_{0}^r\\
&=& \frac{4 \pi}{3} r^3
\end{eqnarray}
というわけで,高校時代なら公式として暗記しておけとでも言われたであろう,円周,円の面積,球の表面積,球の体積が全て直接積分することで求められた。