回転座標系への座標変換
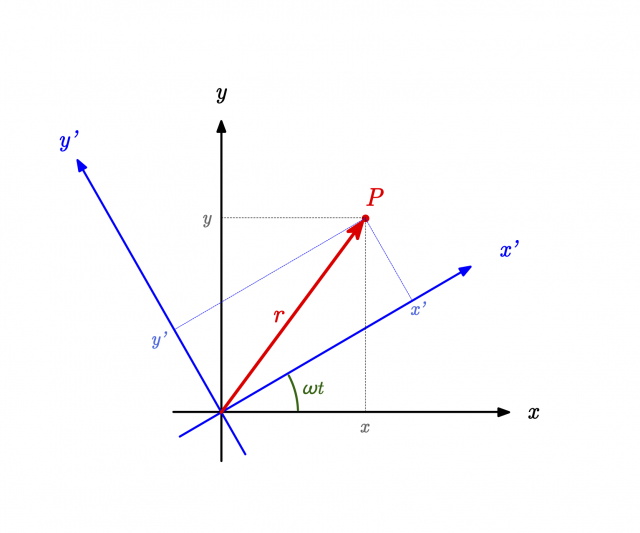
(静止している)慣性系 \(S\) の座標を \((x, y, z)\),\(S\) 系に対して \(z\) 軸のまわりに角速度 \(\omega\) で回転している座標系 \(S’\) の座標 \((x’, y’, z’)\) とすると,座標変換は以下のように表される。
\begin{eqnarray}
x’ &=&x \cos \omega t + y\sin \omega t \\
y’ &=&-x \sin \omega t + y \cos \omega t\\
z’ &=& z
\end{eqnarray}
この逆変換は
\begin{eqnarray}
x &=& x’ \cos \omega t -y’\sin \omega t \\
y &=& x’ \sin \omega t + y’ \cos \omega t\\
z &=& z’
\end{eqnarray}
回転系における基本ベクトル
点 \(P\) の位置ベクトル \(\vec{r}\) は \(S\) 系の基本ベクトルと成分を使って
\begin{eqnarray}
\vec{r} &=& x\,\vec{e}_x + y\,\vec{e}_y + z\,\vec{e}_z \\
&=& (x’ \cos \omega t -y’\sin \omega t)\,\vec{e}_x + (x’ \sin \omega t + y’ \cos \omega t)\,\vec{e}_y +z’\,\vec{e}_z\\
&=& x’ (\cos \omega t\,\vec{e}_x + \sin \omega t\,\vec{e}_y) + y’ ( -\sin \omega t\,\vec{e}_x + \cos \omega t \,\vec{e}_y) + z’\,\vec{e}_z
\end{eqnarray}
一方,回転している \(S’\) 系の基本ベクトルと成分を使って書くと,
\begin{eqnarray}
\vec{r}’ &=& x’\,\vec{e}’_{x} + y’\,\vec{e}’_{y} + z’\,\vec{e}’_{z}\end{eqnarray}
位置ベクトルは座標系の取り方によらない不変な幾何学的オブジェクトであるから,$$\vec{r}’ = \vec{r} $$ このことから,以下のような基本ベクトルの変換式が出てくる。
\begin{eqnarray}
\vec{e}’_x &=& \cos \omega t\,\vec{e}_x + \sin \omega t\,\vec{e}_y\\
\vec{e}’_y &=& -\sin \omega t\,\vec{e}_x + \cos \omega t \,\vec{e}_y \\
\vec{e}’_z &=& \vec{e}_z
\end{eqnarray}
基本ベクトルの時間既存性
静止慣性系 \(S\) の基本ベクトルは時間的に(空間的にも)変化しない
$$\dot{\vec{e}}_x = \dot{\vec{e}}_y =\dot{\vec{e}}_z =\vec{0}$$ としても,回転系 \(S’\) の基本ベクトルは,以下のように時間依存性をもつことがわかる。
\begin{eqnarray}
\dot{\vec{e}}’_x &=& (\cos \omega t\,\vec{e}_x + \sin \omega t\,\vec{e}_y)\dot{} \\
&=& \omega\, (-\sin \omega t\,\vec{e}_x + \cos \omega t \,\vec{e}_y) \\
&=& \omega\,\vec{e}’_y\\
\dot{\vec{e}}’_y &=& (-\sin \omega t\,\vec{e}_x + \cos \omega t \,\vec{e}_y)\dot{} \\
&=& -\omega\, (\cos \omega t\,\vec{e}_x + \sin \omega t\,\vec{e}_y) \\
&=& -\omega\,\vec{e}’_x \\
\dot{\vec{e}}’_z &=&\dot{\vec{e}}_z \\
&=& \vec{0}
\end{eqnarray}
角速度ベクトルの導入
ここで,角速度ベクトル \(\vec{\omega}\) を以下のように導入する:
$$\vec{\omega} \equiv \omega\,\vec{e}’_z \,(= \omega\,\vec{e}_z)$$
すなわち,\(\vec{\omega}\) はベクトルの向きが回転軸とその回転の向き(右ネジの進む向き),大きさ \(|\vec{\omega}| = \omega\) が角速度(の大きさ)に対応しているベクトルである。
基本ベクトルの時間微分を角速度ベクトルを使って表す
基本ベクトル同士の外積が以下のようになることを使うと,
$$\vec{e}’_z \times \vec{e}’_x = \vec{e}’_y, \quad \vec{e}’_z \times \vec{e}’_y = -\vec{e}’_x, \quad \vec{e}’_z \times \vec{e}’_z = \vec{0}$$ 回転系における基本ベクトルの時間微分は,以下のように書ける。
$$\dot{\vec{e}}’_x = \vec{\omega} \times \vec{e}’_x, \quad \dot{\vec{e}}’_y = \vec{\omega} \times \vec{e}’_y, \quad \dot{\vec{e}}’_z = \vec{\omega} \times \vec{e}’_z$$
ちなみに,この最終的な時間微分の式はベクトルで表されているので,座標系のとり方に依存しない。つまり,この式の導出の際には,角速度ベクトル \(\vec{\omega}\) が \(z’\) 軸に平行であることを仮定したが,最終的に導出されたこの式は,\(\vec{\omega}\) がどの方向を向いていても成り立つ一般的な式である。