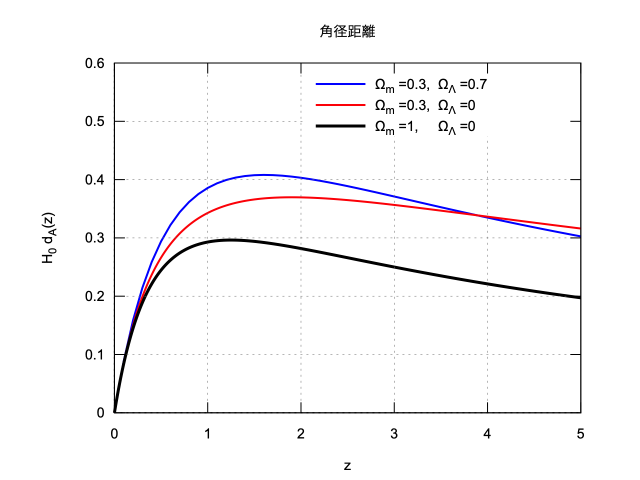
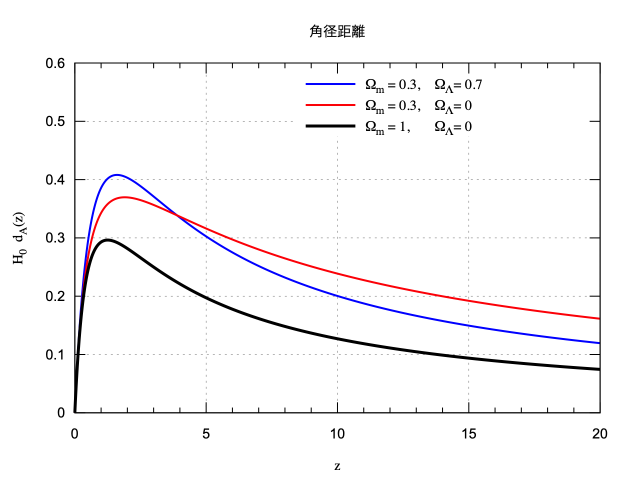
角径距離の導出の詳細については,以下のページを参照。
ここでは,Maxima の plot2d() および draw2d() を使って角径距離のグラフを描く。
$\Omega_{\Lambda} = 0$ の場合の角径距離
\begin{eqnarray}
d_A
&=& \frac{2}{H_0 \Omega_{\rm m}^2 (1+z)^2} \left\{2 – \Omega_{\rm m} + \Omega_{\rm m} z – (2-\Omega_{\rm m}) \sqrt{1 + \Omega_{\rm m} z}\right\}
\end{eqnarray}
以下では $H_0$ を($H_0 = 1$ として)省略し,表記の都合上 $\Omega_{\rm m} \rightarrow \Omega$
dA(Omega, z):= 2/(Omega**2*(1+z)**2) *
(2-Omega+ Omega*z - (2-Omega)*sqrt(1 + Omega*z));
$\Omega_{\rm m} + \Omega_{\Lambda} = 1$ の場合の角径距離
\begin{eqnarray}
d_A
&=& \frac{1}{H_0 (1+z)} \int_0^z \frac{dz}{\sqrt{(1-\Omega_{\rm m}) + \Omega_{\rm m} (1+z)^3} }
\end{eqnarray}
解析的には積分できないので,数値積分 romberg() を使ってみる。
/* 被積分関数の定義 */
f(Omega, z):= 1/sqrt((1-Omega) + Omega*(1+x)**3);
dAL1(Omega, z):= 1/(1+z)*romberg(f(Omega, x), x, 0, z);
quad_qags() で数値積分する関数も定義しておく。quad_qags() は4つの要素
[積分の近似値, 近似の絶対誤差, 被積分関数の評価数, エラーコード]
からなるリストを返すので,積分近似値のみを出力させたい場合には [1] をつけてリストの1番目の要素のみを出力するように指定する。
dAL2(Omega, z):= ((1/(1+z)*quad_qags(f(Omega, x), x, 0, z))[1]);
数値積分の精度を確認するために,$\Omega_m = 0.3, \ z = 1$ の場合の $d_A$ の値を出力。
dAL1(0.3, 1);
dAL2(0.3, 1);
romberg() と quad_qags() で数値積分の値が微妙に異なるのは,romberg() の精度を設定するパラメータ rombergtol のデフォルト値が以下のように少し大きめであることによる。
rombergtol;
パラメータ rombergtol を,より小さい値(例えば rombergtol $= 1.0\times 10^{-10}$)に変更してみると…
rombergtol: 1.e-10;
dAL1(0.3, 1);
dAL2(0.3, 1);
plot2d() でグラフを描く
上記のように数値積分を使って定義した関数 dAL2(Omega, z) を直接
plot2d(dAL2(0.3, z), [z, 0, 5])$
のようにしてグラフを描こうとすると,エラーとなる。
plot2d(dAL2(0.3, z), [z, 0, 5])$
そこで,次善の策として,以下のように数値リストを作り,数値データとして [discrete, listdAL2(0.3)] でグラフにする。
/* z = 0 ~ 20 までのリストを作る関数。*/
listdAL2(Omega) :=
makelist([i*0.1, dAL2(Omega,i*0.1)], i, 0, 200)$
plot2d([[discrete, listdAL2(0.3)],
dA(0.3, z),
dA(1.0, z)],
[z, 0, 5],
/* 縦軸の表示範囲 */
[y, 0, 0.6],
/* 各曲線のオプション:色,線の太さ,凡例。 */
[color, blue,
red,
black],
[style, [lines, 2],
[lines, 2],
[lines, 3]],
[legend, "Ω_m =0.3, Ω_Λ =0.7",
"Ω_m =0.3, Ω_Λ =0",
"Ω_m =1, Ω_Λ =0"],
[xlabel, "z"],
[ylabel, "H_0 d_A(z)"],
[title, "角径距離"],
/* 凡例位置は gnuplot 流に設定。*/
[gnuplot_preamble, "set key Left reverse;"],
/* グラフのサイズ設定 */
[gnuplot_svg_term_command, "set term svg size 640,480 font \",14\""],
/* グリッド */
grid2d
)$
draw2d() でグラフを描く
以下では,Maxima の draw2d() を使ってもう少し $z$ の大きいところまで描いてみる。
draw2d() では,数値積分で定義した関数 dAL2(Omega, z) も文句を言われることなく直接
draw2d(explicit(dAL2(0.3, z), z, 0, 20))$
でグラフを描くことができる。
draw2d(
dimensions=[640, 480], /* グラフのサイズは任意で */
title = "角径距離",
xlabel = "{/Times z}",
ylabel = "{/Times H_0\ d_A(z)}",
/* 表示範囲 */
xrange = [0, 20], yrange = [0, 0.6],
/* 凡例位置等は gnuplot 流に設定。*/
user_preamble = ["set key Left reverse;
set xtics mirror;
set ytics mirror;
set mxtics 5;
set grid;"],
line_width = 2,
key = "{/Times Ω_m = 0.3, Ω_Λ= 0.7}",
color = blue,
explicit(dAL2(0.3, z), z, 0, 20),
key = "{/Times Ω_m = 0.3, Ω_Λ= 0}",
color = red,
explicit(dA(0.3, z), z, 0, 20),
key = "{/Times Ω_m = 1, Ω_Λ= 0}",
color = black,
line_width = 3,
explicit(dA(1, z), z, 0, 20)
)$
$z \gg 1$ での漸近形
$\Omega_{\Lambda} = 0$ の場合
\begin{eqnarray}
d_A
&=& \frac{2}{H_0 \Omega_{\rm m}^2 (1+z)^2} \left\{2 – \Omega_{\rm m} + \Omega_{\rm m} z – (2-\Omega_{\rm m}) \sqrt{1 + \Omega_{\rm m} z}\right\} \\
&\sim& \frac{2}{H_0 \Omega_{\rm m}^2 z^2} \left\{\Omega_{\rm m} z \right\} \\
&=& \frac{2}{H_0\, \Omega_{\rm m}\, z}
\end{eqnarray}
$\Omega_{\rm m} + \Omega_{\Lambda} = 1$ の場合
積分部分をいったん $\displaystyle t = \frac{1}{1+z}, \ dt = – \frac{dz}{(1+z)^2}$ として
\begin{eqnarray}
d_A
&=& \frac{1}{H_0 (1+z)} \int_0^z \frac{dz}{\sqrt{(1-\Omega_{\rm m}) + \Omega_{\rm m} (1+z)^3} } \\
&=& \frac{1}{H_0 (1+z)} \int_0^z
\frac{dz}{(1+z)^2 \sqrt{\frac{\Omega_{\rm m}}{1+z} + \frac{1-\Omega_{\rm m}}{(1+z)^4}} } \\
&\sim& \frac{1}{H_0 (1+z)} \int_{\frac{1}{1+z}}^1
\frac{dt}{\sqrt{\Omega_{\rm m} t}} \\
&=& \frac{1}{H_0 (1+z)\sqrt{\Omega_{\rm m}}} \Bigl[2\sqrt{t} \Bigr]_{\frac{1}{1+z}}^1 \\
&\sim& \frac{2}{H_0\, \sqrt{\Omega_{\rm m}}\,z }
\end{eqnarray}
したがって $0 < \Omega_{\rm m} < 1$ の場合,$z < 1$ では宇宙定数がある場合の角径距離が大きい値を出すにもかかわらず,$z \gg 1$ では宇宙定数がある場合のほうが角径距離は小さくなる。なぜなら,
$$ \frac{1}{\sqrt{\Omega_{\rm m}}} < \frac{1}{\Omega_{\rm m}}\quad \mbox{for}\quad
0 < \Omega_{\rm m} < 1$$
であるから。