Return to 角径距離

補足：Maxima で角径距離のグラフを描く

角径距離の導出の詳細については，以下のページを参照。

ここでは，Maxima の plot2d() および draw2d() を使って角径距離のグラフを描く。

$\Omega_{\Lambda} = 0$ の場合の角径距離

\begin{eqnarray}
d_A
&=& \frac{2}{H_0 \Omega_{\rm m}^2 (1+z)^2} \left\{2 – \Omega_{\rm m} + \Omega_{\rm m} z – (2-\Omega_{\rm m}) \sqrt{1 + \Omega_{\rm m} z}\right\}
\end{eqnarray}

以下では $H_0$ を省略し，表記の都合上 $\Omega_{\rm m} \rightarrow \Omega$

In [1]:
dA(Omega, z):= 2/(Omega**2*(1+z)**2) * 
             (2-Omega+ Omega*z - (2-Omega)*sqrt(1 + Omega*z));
Out[1]:
\[\tag{${\it \%o}_{1}$}{\it dA}\left(\Omega , z\right):=\frac{2}{\Omega^2\,\left(1+z\right)^2}\,\left(2-\Omega+\Omega\,z+\left(-\left(2-\Omega\right)\right)\,\sqrt{1+\Omega\,z}\right)\]

$\Omega_{\rm m} + \Omega_{\Lambda} = 1$ の場合の角径距離

\begin{eqnarray}
d_A
&=& \frac{1}{H_0 (1+z)} \int_0^z \frac{dz}{\sqrt{(1-\Omega_{\rm m}) + \Omega_{\rm m} (1+z)^3} }
\end{eqnarray}

解析的には積分できないので，数値積分 romberg() を使ってみる。

In [2]:
dA1(Omega, z):= 1/(1+z)*romberg(1/sqrt((1-Omega) + Omega*(1+x)**3), x, 0, z);
Out[2]:
\[\tag{${\it \%o}_{2}$}{\it dA}_{1}\left(\Omega , z\right):=\frac{1}{1+z}\,{\it romberg}\left(\frac{1}{\sqrt{1-\Omega+\Omega\,\left(1+x\right)^3}} , x , 0 , z\right)\]

plot2d() でグラフを描く

上記のように数値積分 romberg() を使って定義した関数 dA1(Omega, z) を plot2d(dA1(0.1, z), [z, 0, 5]) のようにしてグラフを描こうとすると，なぜか以下のようなエラーとなる。

In [3]:
plot2d(dA1(0.1, z), [z, 0, 5]);

plot2d: expression romberg(1/sqrt(0.1*(x+1)^3+0.9),x,0.0,z)/(z+1)

    should  depend only on z, or be an expression of 2 variables
    equal another expression of the same variables.


 -- an error. To debug this try: debugmode(true);

そこで，次善の策として，以下のように数値リストを作り，数値データとして points() でグラフにする。

In [4]:
/* z = 0 ~ 20 までのリストを作る関数。*/
rombergtol: 1.E-6$
listdA1(Omega) := makelist([i*0.1, dA1(Omega,i*0.1)], i, 0, 200)$
In [5]:
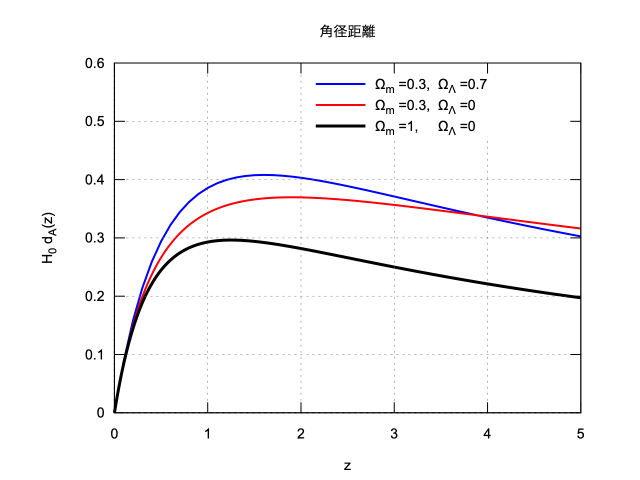
plot2d([[discrete, listdA1(0.0)], 
        [discrete, listdA1(0.3)], 
         dA(0.3, z), 
         dA(1.0, z)], [z, 0, 5], 
       /* 表示範囲 */
       [y, 0, 1.1],                         
       /* 各曲線のオプション：色，線の太さ，凡例。 */
       [color, violet, blue, red, black],                 
       [style, [lines, 2], [lines, 2], [lines, 2], [lines, 3]],         
       [legend, "Ω_m =0,   Ω_Λ =1", 
                "Ω_m =0.3,  Ω_Λ =0.7", 
                "Ω_m =0.3,  Ω_Λ =0", 
                "Ω_m =1.0,  Ω_Λ =0"], 

       [xlabel, "z"], [ylabel, "H0 dA(z)"], [title, "角径距離"], 

       /* 凡例の位置，主目盛・副目盛等の詳細設定は gnuplot 流に設定。*/
       [gnuplot_preamble, "set key left; set key Left reverse;
                           set xtics 1; set mxtics 10;
                           set ytics 0.2; set mytics 4;"], grid2d
)$

draw2d() でグラフを描く

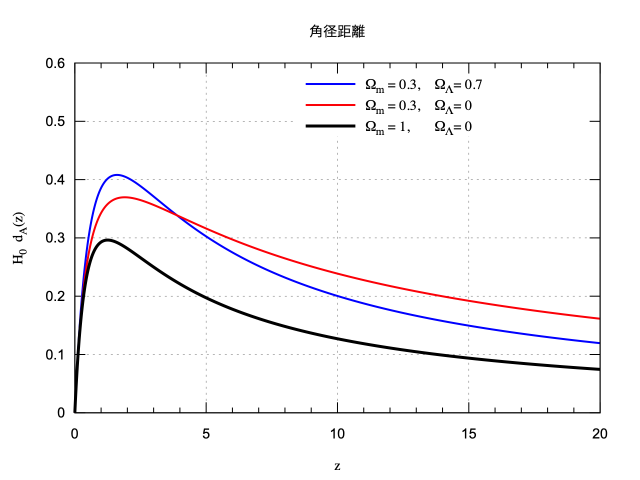
Maxima の plot2d() ではなぜか legend の上付・下付添字が出ないなど若干残念な部分がある。以下では，draw2d() を使ってもう少し $z$ の大きいところまで描いてみる。

また，plot2d(dA1(0.1, z), [z, 0, 5]) はなぜかできなかったが，draw2d(explicit(dA1(0.1, z), z, 0, 5)) はできる。

In [6]:
draw2d(
  title = "角径距離", 
  /* フォント設定は任意。gnuplot 流の定義法。*/
  xlabel = "{/Times:Italic z}", ylabel = "{/Times:Italic H_0\  d_A(z)}", 
  /* 表示範囲 */
  xrange = [0, 20], yrange = [0, 1.3], 
  /* 凡例の位置，主目盛・副目盛等の詳細設定は gnuplot 流に設定。*/
  user_preamble = ["set key top left; set key sample 1; 
                    set key Left reverse;
                    set xtics mirror; set ytics mirror;
                    set xtics 2; set mxtics 4;
                    set ytics 0.2; set mytics 4; set grid;"],

  line_width = 2,
  key = "{/Times Ω_m = 0,       Ω_Λ= 1}", 
  point_type = dot,
  points_joined = true,
  color = magenta,
  explicit(dA1(0.0, z), z, 0, 20), 
  
  key = "{/Times Ω_m = 0.3, Ω_Λ= 0.7}", 
  point_type = dot,
  points_joined = true,
  color = blue,
  explicit(dA1(0.3, z), z, 0, 20), 
  
  key = "{/Times Ω_m = 0.3,    Ω_Λ= 0}", 
  color = red,
  explicit(dA(0.3, z), z, 0, 20), 
  
  key = "{/Times Ω_m = 1,       Ω_Λ= 0}", 
  color = black,
  line_width = 3,
  explicit(dA(1, z), z, 0, 20)
)$

$z \gg 1$ での漸近形

$\Omega_{\Lambda} = 0$ の場合

\begin{eqnarray}
d_A
&=& \frac{2}{H_0 \Omega_{\rm m}^2 (1+z)^2} \left\{2 – \Omega_{\rm m} + \Omega_{\rm m} z – (2-\Omega_{\rm m}) \sqrt{1 + \Omega_{\rm m} z}\right\} \\
&\sim& \frac{2}{H_0 \Omega_{\rm m}^2 z^2} \left\{\Omega_{\rm m} z \right\} \\
&=& \frac{2}{H_0\, \Omega_{\rm m}\, z}
\end{eqnarray}

$\Omega_{\rm m} + \Omega_{\Lambda} = 1$ の場合

積分部分をいったん $\displaystyle t = \frac{1}{1+z}, \ dt = – \frac{dz}{(1+z)^2}$ として

\begin{eqnarray}
d_A
&=& \frac{1}{H_0 (1+z)} \int_0^z \frac{dz}{\sqrt{(1-\Omega_{\rm m}) + \Omega_{\rm m} (1+z)^3} } \\
&=& \frac{1}{H_0 (1+z)} \int_0^z
\frac{dz}{(1+z)^2 \sqrt{\frac{\Omega_{\rm m}}{1+z} + \frac{1-\Omega_{\rm m}}{(1+z)^4}} } \\
&\sim& \frac{1}{H_0 (1+z)} \int_{\frac{1}{1+z}}^1
\frac{dt}{\sqrt{\Omega_{\rm m} t}} \\
&=& \frac{1}{H_0 (1+z)\sqrt{\Omega_{\rm m}}} \Bigl[2\sqrt{t} \Bigr]_{\frac{1}{1+z}}^1 \\
&\sim& \frac{2}{H_0\, \sqrt{\Omega_{\rm m}}\,z }
\end{eqnarray}

したがって $0 < \Omega_{\rm m} < 1$ の場合，$z < 1$ では宇宙定数がある場合の角径距離が大きい値を出すにもかかわらず，$z \gg 1$ では宇宙定数がある場合のほうが角径距離は小さくなる。なぜなら，

$$ \frac{1}{\sqrt{\Omega_{\rm m}}} < \frac{1}{\Omega_{\rm m}}\quad \mbox{for}\quad
0 < \Omega_{\rm m} < 1$$

であるから。