見かけの光度が距離の2乗に反比例することから定義される光度距離について,一般的な定義から説き起こす。
必要な式のおさらい
幾何光学近似
ここでまとめているように,4元ベクトル $k^{\mu}$ で表される「単色光」の光源天体から放出される,電磁場のエネルギー運動量テンソルは
$$T^{\mu\nu} = A^2 k^{\mu}k^{\nu}$$
$T^{\mu\nu}_{\ \ \ ;\nu}=0$ より
$$A_{,\nu} k^{\nu} + \frac{1}{2} A k^{\nu}_{\ \ ;\nu} = 0$$
ちなみに,ヌル測地線のアフィンパラメータ $v$ を使うと,
$$A_{,\nu} k^{\nu} = \frac{dx^{\nu}}{dv} \frac{\partial}{\partial x^{\nu} }A = \frac{d A}{dv}$$であるので
$$\frac{d A}{dv} + \theta A = 0$$と書いた方が見通しが良いかも知れない。$\theta$ は光線束の expansion。
$k^{\mu}$ はうずなしのヌル測地線である。
$$
k_{\mu, \nu} – k_{\nu, \mu} = k_{\mu; \nu} – k_{\nu; \mu} =0
$$
$$ k_{\mu} k^{\mu} = 0, \quad k^{\mu}_{\ \ ;\nu} k^{\nu} = 0$$
観測者の4元速度に基づいた \(k^{\mu}\) の $3+1$ 分解
$$k^{\mu} = \frac{dx^{\mu}}{dv} = \omega ( u^{\mu} + \gamma^{\mu})$$
ここで,$\omega$ は4元速度 $u^{\mu}$ の観測者が観測する光の振動数であり
$$\omega \equiv – k_{\mu} u^{\mu}$$
また,$\gamma^{\mu}$ は $u^{\mu}$ に直交する空間的単位ベクトルであり,
$$u_{\mu} u^{\mu} = -1, \quad u_{\mu} \gamma^{\mu} = 0, \quad \gamma_{\mu} \gamma^{\mu} = 1$$
光源天体からのエネルギー流束
4元速度 $u^{\mu}$ の観測者が観測する,光源天体からのエネルギー流束 $f^{\mu}$ は
\begin{eqnarray}
f^{\mu} &=& \left(g^{\mu\alpha} + u^{\mu} u^{\alpha} \right) T_{\alpha\beta} u^{\beta}\\
&=& A^2 \omega^2 \gamma^{\mu} \\
&\equiv& f \gamma^{\mu}
\end{eqnarray}
ここで $f = A^2 \omega^2$ は $\gamma^{\mu}$ に垂直な面に対するエネルギー流束(単位面積単位時間あたりのエネルギーの流れ)であり,絶対光度 $L$ の光源天体に対して,4元速度 $u^{\mu}$ の観測者が観測する見かけの光度に相当する。
光度距離の定義
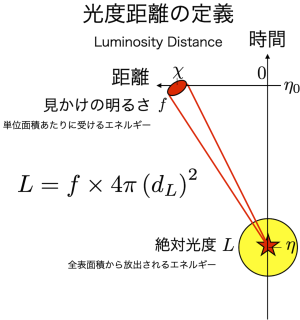
絶対光度 $L$ とはすなわち,光源を囲む全表面積から放出されるエネルギーのこと。見かけの明るさ $f$ とは,単位面積あたりに受けるエネルギー。$f$ に全表面積をかけると $L$ になる。そこで,光源までの(光度)距離を $d_L$とすると,半径 $d_L$ の球面の全表面積は $4 \pi \left( d_L\right)^2$ であるから
\begin{eqnarray}
L &=& f \times 4 \pi \left( d_L\right)^2\\
\therefore\ \ f &=& \frac{L}{4 \pi \left( d_L\right)^2}
\end{eqnarray}
このように,見かけの光度が距離の2乗に反比例することから,
$$ f \equiv \frac{L}{4\pi \left(d_L\right)^2}$$
で定義される距離 $d_L$ が光度距離と呼ばれる。
エネルギー流束 $f$ の式を入れると
\begin{eqnarray}
A^2 \omega^2 &=& \frac{L}{4\pi \left(d_L\right)^2} \\
\therefore \ \ A \omega d_L &=& \sqrt{\frac{L}{4\pi}} = \mbox{const.}\\
\frac{d}{dv} \left(A \omega d_L \right) &=& 0 \\
\therefore \ \ \frac{d}{dv}\left( \omega d_L\right) &=& -\frac{1}{A} \frac{dA}{dv} \left( \omega d_L\right) \\
&=& \theta \left( \omega d_L\right)
\end{eqnarray}
光源における振動数を $\omega_e$ とすると,共動観測者が観測する振動数 $\omega$ は赤方偏移 $z$ を使って以下のように書ける。
$$\omega = \frac{\omega_e}{1+z}$$
これを使うと,光度距離を決める式は
$$\frac{d}{dv}\left( \frac{d_L}{1+z}\right) = \theta\left( \frac{d_L}{1+z}\right)$$
光度距離の観測(角径距離と比較して)
以下で紹介するが,光度距離と角径距離は独立な距離公式ではなく,任意の時空において
$$d_L(z) = (1+z)^2 \, d_A(z)$$
という関係があることが知られている。これを reciprocity theorem と呼んだりする。以下の文献に証明がある。
- G. F. R. Ellis – Relativistic Cosmology, in “General Relativity and Cosmology” ed. B. K. Sachs (Academic Press, New York, 1971)
なので,同一天体に対して光度距離と角径距離を独立に観測で求めることは,単に reciprocity theorem の確認,または一般相対性理論が成り立っていることの確認となるだけである。
観測的には,角径距離は遠方天体の大きさ・サイズを観測する必要があるため,観測装置の分解能で大きさがわかるようなサイズの観測対象が必要である。一方,光度距離は光度のみが観測されれば良いため,遠方の暗い天体でも十分な露出時間と高感度な撮影素子があれば観測可能である。
ただし,天体の見かけの明るさの観測から光度距離を求めるためには,その天体の絶対光度がわかっていることが必要である(standard candle, 標準光源)。何らかの方法で遠方天体の絶対光度が推定できれば光度距離が求まり,宇宙論パラメータも決まることになる。
また,観測量に基づいた種々の宇宙論的距離は大体 $(1+z)^n$ のファクターのみの違いしかなく,同等な観測量となってしまうが,唯一,parallax distance が独立な距離公式となっている。parallax distance は文字通り「視差」の観測,つまり三角測量から決まる宇宙論的距離公式であり,遠方天体の固有量(絶対光度とか固有の大きさとか)が必要ない。このへんは昔,以下の論文に書いた。
「三角測量」=「Triangulation」ということで気張ったタイトルをつけたが全然はやらなかった orz し,全然違う意味で Triangulation が他の文献で使われているような気がする…
FLRW 宇宙における光度距離
FLRW 時空において,
- アフィンパラメータ $v = 0$,時刻 $\eta(0) = \eta$ に
- 動径座標 $\chi(0) = 0$ で
- 赤方偏移 $z$ の光源天体から動径方向に放出された
- 振動数 $\omega_e$ の光を,
- アフィンパラメータ $v = v_0$,時刻 $\eta(v_0) = \eta_0$ に
- 動径座標 $\chi(v_0) = \chi$ で
- 4元速度 $u^{\mu}$ の共動観測者が振動数 $\omega$ の光として観測する
として,その際の光度距離 $d_L$ を求める。
まず,動径方向に伝播するヌル測地線の解
$$k^{\mu} = (k^0, k^1, 0, 0) = \left(\frac{\omega_c}{a^2}, \frac{\omega_c}{a^2}, 0, 0\right)$$を使うと,
\begin{eqnarray}
k^{\mu}_{\ \ ;\mu} &=& \frac{1}{\sqrt{-g}}\left( \sqrt{-g} k^{\mu}\right)_{, \mu} \\
&=& \frac{1}{a^4\sigma^2} \left\{(a^4 \sigma^2 k^0)_{, 0} + (a^4 \sigma^2 k^1)_{, 1} \right\}\\
&=& \frac{1}{a^2 \sigma^2} \left\{k^0 (a^2\sigma^2)_{,0} + k^1 (a^2\sigma^2)_{,1} \right\}\\
&=& \frac{1}{a^2 \sigma^2} \frac{d}{dv} (a^2\sigma^2) \\
&=& \frac{2}{a \sigma} \frac{d}{dv} (a \sigma)
\end{eqnarray}
となり,これから光度距離を決める式は
$$\frac{1}{\left( \frac{d_L}{1+z}\right)} \frac{d}{dv} \left( \frac{d_L}{1+z}\right) = \frac{1}{a \sigma} \frac{d}{dv} (a \sigma)$$
これはただちに積分できて,積分定数 $C$ を使って
$$\frac{d_L(v)}{1+z} = C \, a(\eta(v))\, \sigma(\chi(v))$$
となる。$d_A$ の場合と同様に,積分定数 $C$ は,後の結果を使って
$$ d_L \simeq \frac{1}{H_0} z\quad\mbox{for}\ \ |z| \ll 1$$
となるように $C=1$ と選んでおこう。アフィンパラメータ $v$ と座標 $\eta, \, \chi$ の関係は,$v = 0$ で$\eta(0) = \eta, \, \chi(0) = 0$,$v = v_0$ で $\eta(v_0) = \eta_0, \, \chi(v_0) = \chi$ となるようにとるので,
\begin{eqnarray}
d_L(v_0) &=& (1 + z) a(\eta_0) \sigma(\chi)\\
&=& (1 + z) \frac{a_0}{a(\eta)} a(\eta)\sigma(\chi)\\
&=& (1 + z)^2 d_A
\end{eqnarray}
すなわち,光度距離 $d_L$ は角径距離 $d_A$ に $(1+z)^2$ をかけたものになる。