前記事（データ生成編）で生成した2タイプの仮想計測データに対して、指数関数フィッティングを2通りの方法で行います。データのもつ不確かさの性質に応じて、最適なフィッティング方法が変わることを見ていきます。
解析
前記事で用意した計測データに対して、指数関数 
へのフィッティングを行い、パラメータa,bを決定します。指数関数へのフィッティングを行う場合は、特にaのパラメータに興味がある場合が多いので、2つの方法で求めたaの値に着目し、それがどのような分布をとるかを見ていきます。
各タイプ100セットのデータについて手作業で解析するのは大変ですので、スクリプトで処理しました。詳細は付録で説明します。
「対数線形近似」については解析的に求められるので、普通に計算するだけです。「文字通りの最小二乗法」では数値計算のような処理が必要になります。自分で書くのはしんどいので、スクリプトからR言語の処理系（GNU R）を呼び出して処理しました。
評価
得られたaについてのヒストグラムを描いてもいいのですが、ここでは2つの方法によるaの値を縦軸と横軸にとることで、両者の分布をまとめて観察します（相関関係も見ることができます）。モデルのaは-0.232でしたのでそれを真値として、真値をどの程度精密に推定できるかを見ていきます。
「精密さ」の他に「正確さ」という基準もあります。簡単に言うと、分布の中心（平均）が真値とどのくらい近いか（一致すると言えるか）ということです。結論だけ言うと、今回見ていくaの分布については、いずれも真値を中心に分布していると考えることができます（分布の中心と真値の間に有意差がない、ということ）。よってこれ以降では主に「精密さ」についての評価を行います。
まずは、絶対不確かさが一定の場合を図4に示します。
図1（データ生成編で提示しています）においてオレンジで示した計測データのセットに対して、「文字通りの最小二乗法」で求めたaは-0.2315でした。一方、同じ計測データのセットに対して、「対数線形近似」で求めたaは-0.2364でした。そこで、横軸の-0.2315、縦軸の-0.2364に点を打っています（この点だけはオレンジで示しています）。他の99セットに対しても同じように考えて、青い点を打っています。
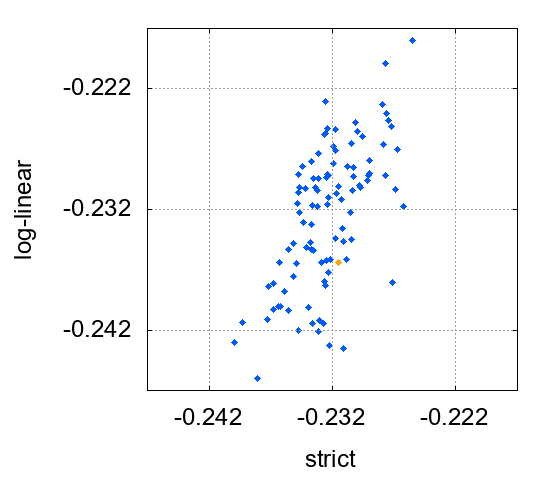
横軸に「文字通りの最小二乗法」で推定したaの値、縦軸に対数線形近似で推定したaの値をプロットしています。
横軸、縦軸ともに、真値である-0.232を中心に分布していると見てよさそうです。そして、プロットが縦長に分布しているのがわかります。これは、「文字通りの最小二乗法」による推定値の方が散らばりが小さい、すなわち精度が高いことを意味しています。
散らばりの大きさを定量的に評価するために、誤差（推定値-真値）の二乗平均平方根（いわゆるRMS）を求めると、「対数線形近似」では0.0058なのに対して「文字通りの最小二乗法」では0.0029となっています。
次に、相対不確かさが一定の場合を図5に示します。
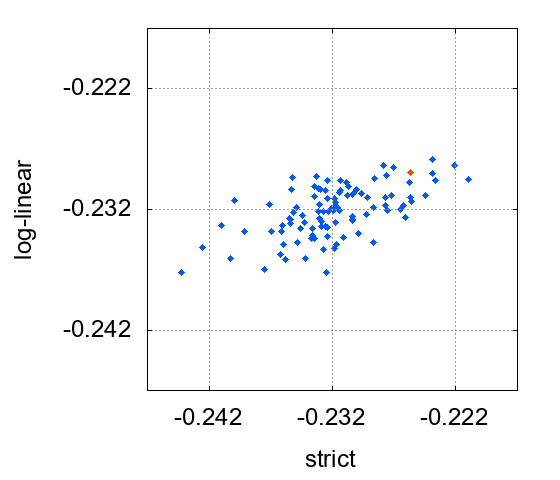
同じようにプロットしました。今度は逆に縦軸方向の散らばりが小さくなっています。これは、「対数線形近似」による推定値の方が精度が高いことを意味します。RMS誤差は「対数線形近似」で0.0021、「文字通りの最小二乗法」で0.0042でした。いずれについても片方のRMS誤差が他方の2倍になっているのは、何か必然性があるのでしょうか？私の直感は偶然の産物だと言っていますが…
まとめ
指数関数フィッティングの2つの方法をどういうケースで使い分けるのがいいか、という問題について、仮想の計測データを用意して検証しました。計測データのもつ不確かさの性質に応じて以下のように使い分けることで、より精度の高いフィッティング結果を得ることができました。
- 絶対的な不確かさが一定の場合は、文字通りの最小二乗法を用いる。
- 相対的な不確かさが一定の場合は、対数をとった上で線形近似を行う。
付録・フィッティング処理を行うスクリプト
フィッティング処理を行うスクリプトを、2方法のそれぞれについてRuby(+α)で作成しました。こちらもGistにソースコードを公開しておきます。
対数線形近似
簡単な方から見ていきます。こちらは縦軸についての対数をとり、最小二乗法で1次関数にフィッティングさせます。これは解析的に処理できますので、解析的に求めた式にデータの値を代入するだけです。
文字通りの最小二乗法
こちらは数値計算的な処理が必要になりますので、真面目に実装しようとすると大変です。そこで、統計分野において実績と信頼のあるGNU R（R言語の処理系。実質的に唯一の処理系であることから、単に「R言語」と言われることも多い）の力を借りることにします。
RubyからGNU Rの力を借りる方法ですが、強く確立したものはないような気がします。ここでは、とりあえず目が合ったr_bridgeというライブラリを使っています。
こういうところが、Pythonと比べたときのRubyの弱さですね。個人的にPythonの言語仕様というか構文がどうにも馴染まないので、心温まるRubyがこういう用途で使いやすくなるとうれしいのですが…。同様のライブラリがいくつか見つかった中でr_bridgeと目が合ったのは、最新版が最も新しかったからです（バージョン0.5.1が2020-12-04にリリースされています）。なお、Windowsではr_bridgeが依存しているlibffiとの連携がうまくできなかったので、こちらのスクリプトだけはWindows Subsystem for Linux(WSL)のUbuntuで実行しました。Windowsでも実行できるようにこの記事を煮詰めたかったのですが、年内に間に合いませんでした。
ということで、あとはほとんどR言語の話になります。今回のような非線形の最小二乗法を行うには、nlsという関数を使います。そしてこの関数には、最適化したいパラメータの初期値を与える必要があります。与える初期値によっては、フィッティングの結果が変わる（あるいは不適切な結果を返す）場合があります。今回は、”真値”にほどよく近い値として、a=-0.2、b=250を与えました。そのため、不適切な結果が返ってくることはありませんでした。
出力ですが、これはGNU Rの出力をそのまま保存する方法しか見つかりませんでした。これは1セットのデータについて2行を出力した、次のような形式になります。
a b
-0.2323186 249.5110300
a b
-0.2317661 250.2452691
a b
（以下省略） a bの行が毎回出力されるのが邪魔になります。これは手作業で（正規表現による置換処理が可能なテキストエディタで、の意）除去しました。