前回までのシリーズ「指数関数でフィッティングしても残差平方和が最小にならない」（前編＋後編）のスピンアウト的な記事になります。仮想的な計測データに対して2つの方法での指数関数フィッティングを試みて、どちらの方法がよさそうかを見てみます。
例によって大河記事になりましたので、2編に分けました。まずはこちらのデータ生成編です（結論は解析編で述べています）。仮想的な計測データを用意するところまでの手順を述べていきます。
前回までのあらすじと今回の目標
測定データに対して指数関数フィッティングを行う場合、2つの方法が主に使われます。
- 残差平方和が最小になるように（数値計算で）パラメータを求める（文字通りの最小二乗法）
- 対数をとった上で線形近似する（対数線形近似）
そして後編では、両者の使い分けとして次のように書きました。
つまり、測定値がその大きさに関係なく一定の不確かさをもつと考えられる場合には、「文字通りの最小二乗法」を使うのが妥当であると言えます。一方で、測定値がその大きさに比例するような不確かさをもつ（すなわち相対不確かさが一定である）と考えられる場合には、「対数線形近似」を使うのが妥当であると言えます。
わかる人にはわかる説明ですが、この前後を含めて読んでも「どこが”つまり”なんだ？」と思う人もいれば、「なんとなくそんな気もするけど、ほんまかいな？」と思う人もいるでしょう。前者の人々の腑に落とす説明をする力は今の私にはありませんが、主に後者の人々に向けて、仮想的な測定データに対して解析を行うことで、上記の記述の妥当性を示すことを今回（本記事＋次記事）の目標にします。
仮想的な計測データの準備
本記事では計測データはすべて仮想的なものですので、以後「仮想的な」を省略します。
ここでは、
というモデルに従う系を想定します。xを0から10までの値に0.5間隔で設定して（xは正確に設定できるものとします）、それぞれに対するyを計測しますが、yの計測には不確かさをともないます（また不確かさを含んだ計測値は、互いに独立であるとします）。21点の計測データを指数関数でフィッティングして、aの値を推定することが目的です。
計測の不確かさは疑似乱数（以下では単に「乱数」と表記）で実現しますが、次の2タイプの不確かさを用意します。
- 真値の大きさにかかわらず、σ=3の正規分布に対応する不確かさをもつ（絶対不確かさが一定）
- 真値の大きさの3%をσとする正規分布に対応する不確かさをもつ（相対不確かさが一定）
たとえば、x=0に対しては、y=251が真値となります。しかし計測値としては、絶対不確かさが一定の場合ですと、平均が251、分散が9（3の二乗）の正規分布に従う乱数から得た値とします。他のxについても同様にして値を取得し、21点の計測値を1セットとします。それを繰り返して、上記の2タイプについてそれぞれ100セットの計測データを用意しました。
それぞれの散布図を見ながら、意図した通りの計測データが得られたことを確認しましょう。まず、絶対不確かさが一定の場合について図1に示します。
特定の1セットの計測データをオレンジでプロットしています。他の99セットの計測データについても同じようにプロットして、それらをすべて空色で表示しています。空色の帯の長さを見ることで、それぞれのxについての計測値の散らばりを知ることができます。
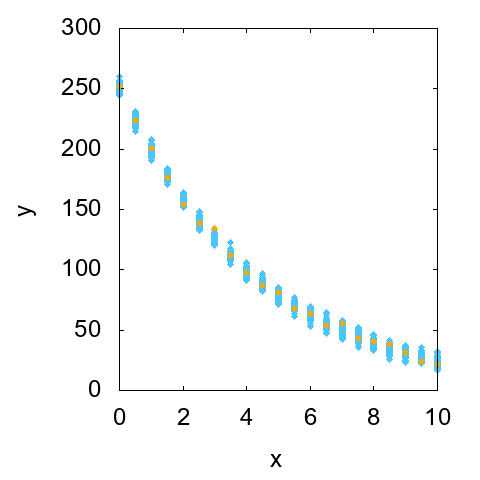
この場合は、それぞれのxについて100個のyの値が同じような散らばり方をしていることが見て取れます（細かい分布まではわかりませんが、散らばりの幅が同程度であることはわかるでしょう）。
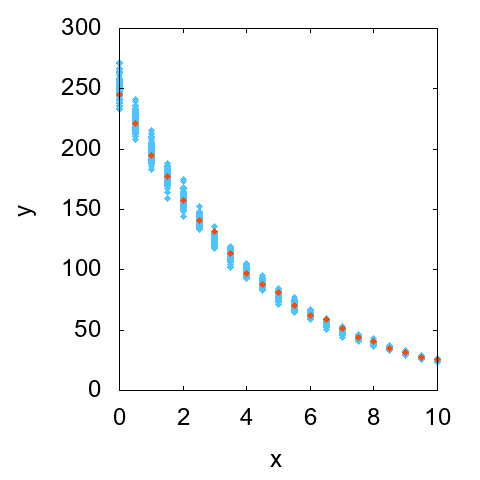
続いて相対不確かさが一定の場合の散布図を図2に示します。こちらはxの値が大きいほどyの散らばりの幅が大きくなっているのが見て取れます。ついでに、縦軸を対数スケールにした散布図も見ておきます（図3）。
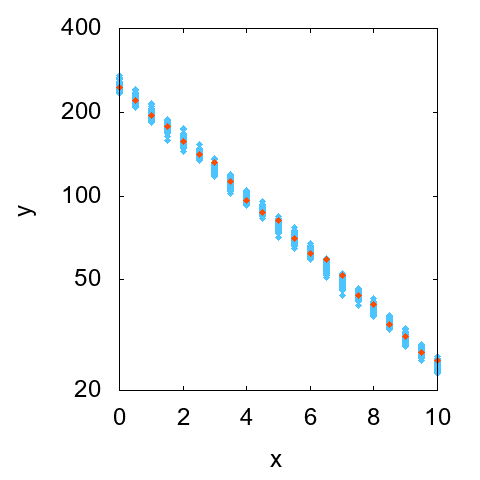
こちらでは、yの散らばりの幅が同程度になっています。これは、それぞれのxに対する計測値の相対不確かさが同程度であることを意味します。ということで、いずれのケースについても、意図したとおりの計測データが得られていることがわかりました。
次記事予告
計測データが用意できたので、あとはフィッティングを試みるだけです。が、それは次記事に引っ張ります。本記事の残りでは、実際にどうやって計測データをこしらえたのかを、付録として述べておきます。
付録・計測データを生成するスクリプト
今回は、Rubyのスクリプトを用いて計測データを用意しています。そもそも私がスクリプトというときは、ほとんど全てがRubyのスクリプトです。
とりあえずソースコードを見たいという方は、以下のGistをご覧下さい。
核心と言えるのは、「いかにして標準正規分布に従う乱数を得るか」というところですので、以下で詳説します。それ以外は単純なファイル入出力ですので、面倒な部分はあるものの、難しくはないでしょう。
標準正規分布に従う乱数を得る
標準的な言語の処理系には、疑似乱数を得るライブラリが標準で使えるようになっています。Rubyにおいても、Randomモジュールが組み込まれており、特段の宣言などがなくても利用できます。しかし、これらのモジュールが提供する乱数は、通常は一様分布（0以上1未満）に従う乱数です。標準正規分布に従うような乱数を得るにはどうすればいいでしょうか？（標準正規分布に従う乱数が得られれば、それを線形変換することで、任意の正規分布に従う乱数を得ることができます。）
まずは、一様分布から得た乱数を標準正規分布の累積分布関数の逆関数に放り込む、という方法が考えられます（表計算ソフトでは、=NORM.S.INV(RAND())をよく使いますね！）。しかし、正規分布については、累積分布関数の逆関数を初等関数で表すことができない（＝数値計算的な手法が必要になる）という問題点があります。（ちなみに、例えば指数分布については、これを初等関数だけで表すことができます。）
そういう事情もあって、この目的ではボックス・ミュラー法がよく使われます。詳細はリンク先「高校数学の美しい物語」にお任せするとして、これを1行で説明すると、一様分布から得た2つの（独立な）乱数を使って、標準正規分布に従う（独立な）乱数を2つ得る、というものです。一見しただけでは「ペアとして得られた2つの乱数が独立ではないのでは？」と心配になってしまいますが、きちんと独立になっていることが証明されていますので、安心して使うことができます。
もしかしたらこの乱数を提供するライブラリがあるのかもしれませんが、簡単に実装できますので、自分でこしらえてみたものが上記のリンク先になります。