汎用的な表計算ソフトで2つの量（あるいは数）の関係を指数関数でフィッティングしても、それが残差平方和を最小にするものにならない、というケースを前編の記事で見ました。
後編では、どうしてそういうことが起こるのか、そしてその現象についてどう考えるべきなのか、という話をしていきます。

指数関数近似の方法

最小二乗法について述べている書籍を見ると、指数関数でフィッティングする場合には、残差平方和を最小にするような指数関数のパラメータを求める代わりに、縦軸の値の対数をとったものに対して線形近似（すなわち、1次関数の2つのパラメータを最小二乗法で最適化する）を行う方法が述べられています（片対数軸でプロットすると直線状に並ぶのでそれを直線で近似する、ということですね！）。つまり、指数関数でフィッティングさせる方法には、主に以下の2つがあるということです。

1. 残差平方和を最小にする（以下「文字通りの最小二乗法」と呼ぶ）
2. 縦軸の値の対数をとり、その残差平方和を最小にする1次関数を求める（以下「対数線形近似」と呼ぶ）

これはすごくすごく大事なのに触れられていない場合があるのですが、この両者は等価ではありません。それにもかかわらずわざわざ「対数線形近似」が取り上げられることが多いのは、「対数線形近似」では解析的に解が求められるという長所があるからだと推測します。「文字通りの最小二乗法」では解析解を得るのが困難（不可能？）なため、数値計算的に解を求めるしかありません。

表計算ソフトにおける指数関数近似の実装

LibreOfficeにおいて、指数関数近似をどのようなアルゴリズムで行っているのかを見てみましょう。

※ここで行うのは、挙動から実装を推測する、という話です。LibreOfficeの場合はオープンソースですので実装を確認することが理論的には可能です。しかし、誰もがそれにアプローチできるスキルを持っているわけではないでしょう。また、MS Excelのようにオープンでないソフトに対してはそのアプローチは使えません。ドキュメントにおいても、実装に関する十分な説明はなされていません。

指数関数近似の結果が残差平方和を最小にしていないことを前編で見ました。そのため「文字通りの最小二乗法」で求めているのではないことがわかります。それでは「対数線形近似」を行っているかどうかを確認してみましょう。

y（縦軸）の自然対数をとった列を用意し、xとその列について線形近似を行います。（散布図を描いてもいいのですが、ここではslope関数とintercept関数を使っています。）

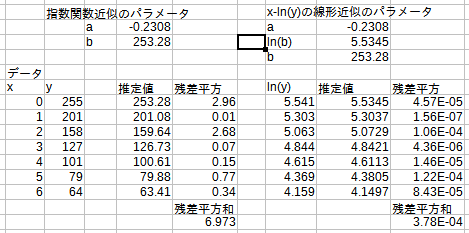
その結果が図1の右半分になります。はい、グラフから行ったフィッティングと全く同じパラメータa,bが得られました。念のため述べると、この2つのパラメータは紛れもなく残差平方和を最小にしています。

ということで、LibreOfficeが指数関数近似を行う際には「対数線形近似」を行っていることがわかりました。やはり解析的に解が得られるというメリットが大きいので、こちらの方法を採用しているのでしょう。MS Excelについても、同様の手順で同様の結論が得られるはずです。

どちらが妥当なのか

測定データを指数関数にフィッティングするアルゴリズムとして、「文字通りの最小二乗法」と「対数線形近似」の2つの方法があり、両者は一般に異なる結果を返すことがわかりました。それでは、どちらを使うのが妥当なのでしょうか？

指数関数でフィッティングさせる方法は他にもありますが、本記事ではこの2つに絞って話を進めます。

簡単に答えると、それはケースバイケースです。もう少し詳しく答えると、yの測定値の不確かさがどのような性質を持つのかに依存します。すなわち、測定値の大きさに関係なく一定の不確かさをもつのか、それとも測定値の大きさに比例するような不確かさをもつのかということです。

「文字通りの最小二乗法」では、文字通りの残差の2乗和を最小にしています。つまり、50に対する1の差と、200に対する1の差を同等に評価します。一方の「対数線形近似」では、残差の比（残比？）をもってフィッティングを評価しています。50に対する1の差（2%）よりも、200に対する1の差（0.5%）を小さいと評価します。大きい値のデータに対しては残差が大きくてもペナルティが少ないのですが、小さい値のデータに対する残差にはシビアになります。

つまり、測定値がその大きさに関係なく一定の不確かさをもつと考えられる場合には、「文字通りの最小二乗法」を使うのが妥当であると言えます。一方で、測定値がその大きさに比例するような不確かさをもつ（すなわち相対不確かさが一定である）と考えられる場合には、「対数線形近似」を使うのが妥当であると言えます。

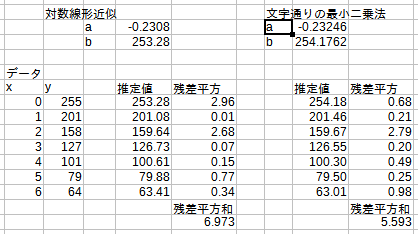
前編で取り上げたフィッティング例を図2に再掲しました。これらの結果で残差平方の大きいデータに着目してみましょう。「対数線形近似」では、x=0のデータについての残差平方が大きく、これが「文字通りの最小二乗法」と比べたときの残差平方和の大きさに寄与しています。値の小さなデータについての残差についてシビアな「対数線形近似」においては、x=0の残差平方を大きくしてでも、値の小さなx=4やx=6の残差平方を小さくすることに大きなウェイトが置かれている、ということです（x=5では逆に大きくなっていますが）。

まとめ

表計算ソフトで指数関数近似した結果は、一般に残差平方和を最小にするものではありません。だからといって、それがインチキだということではありません。特に測定値の相対不確かさが一定であるような場合は、表計算ソフトによるその結果がより妥当であると言えます。

大事なことは、どういう方法で得られたパラメータであるのかを、使った人が正しく認識することです。たとえば報告書などで単に「残差二乗和が最小になるように指数関数でフィッティングした」と書いておきながら「対数をとって線形近似した」結果を載せてしまうと、それは嘘を述べていることになります。結論自体に大きな影響はなかったとしても、報告書自体に対する信頼（ひいては報告者に対する信頼）というのはそういうところから失われていくものだったりします。

関連サイト

(2020-12-07:追加)

• エクセル近似曲線の罠 – 小人さんの妄想 : R言語で「文字通りの最小二乗法」を使って求めています