実験題目「ばね振り子の振動」では，振動の大きさ（実は変位の微分，すなわち速度に相当する）をデジタルオシロスコープで記録しますが，そのデータをUSBメモリを介してエクスポートすることができます．以前紹介したLibreOffice Calc でのフーリエ解析の例として（そしてLibreOffice 6.3 のリリース記念として），そのデータを解析してみました．

画面上で振動数を求める

まずは実験でも行うように，デジタルオシロスコープの画面（Fig.1）から振動数を求めてみましょう．

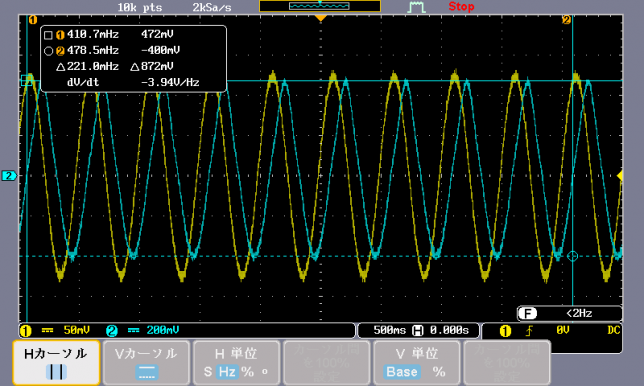
（ここでは水色のCh2がばね振り子の振動に対応しています．）できるだけ画面を幅いっぱいつかって，9周期分の時間を測定しています．ここではカーソルに対応する振動数として 221.0 mHz と表示されていますが，ばね振り子の振動数はこれの9倍なので 1.989 Hz となります．ちなみに（このあたりでの）刻み幅は 0.1 mHz でしたので，4桁目も有効数字と考えていいでしょう．

フーリエ解析で振動数を求める

この波形をそのままエクスポートしてフーリエ解析したくなります（というか，しました）が，そこに落とし穴があります．離散フーリエ変換の出力の周波数分解能がどうなるのかを忘れがちですが，変換前のデータ長（時間単位）の逆数になるのでした．いま表示されているのは，5秒間の波形ですから，それをフルに使ってフーリエ変換しても，周波数の分解能は 0.2 Hz しかありません．それでは今回の測定にはちょっと物足りません．たとえば 0.01 Hz の分解能を要求すると，100秒間のデータを表示させる必要があります．今回はさらに2倍の，200秒間のデータをエクスポートしましょう．オシロスコープの画面では Fig.2 のようになります（カーソルは関係ないので，消しておけばよかったですね）．

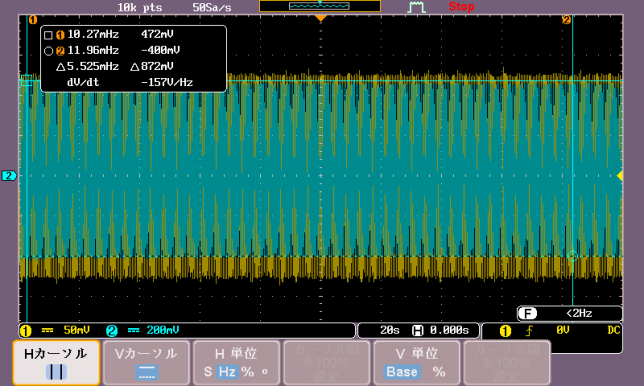
200秒間安定した振動をするのは当然のことだと思っていましたが，途中で振幅が大きくなるケースがあったりして，このデータにありつくまでは10分近くかかったような記憶があります．また，画面上部にも書いてありますが，基本的には画面いっぱいの時間幅を10000等分してサンプリングしているようです（これは100000などに変更できるようですが，ここではその周辺の設定は変更していません）．

それではフーリエ解析を実行してみましょう．データは10000点ありますが，フーリエ変換を行うにあたっては始点と終点を同じような位相のところにするのが望ましいので，前後をカットして9871点のデータに対してフーリエ変換を行っています．フーリエ変換を行うデータ数の制限がないので，純粋にデータだけを見て範囲を決定することができます．そういう事情もあって（また私がよくわかっていないのもあって），フーリエ変換の際によく出てくる窓関数はここでは使っていません．その結果が Fig.3 になります．

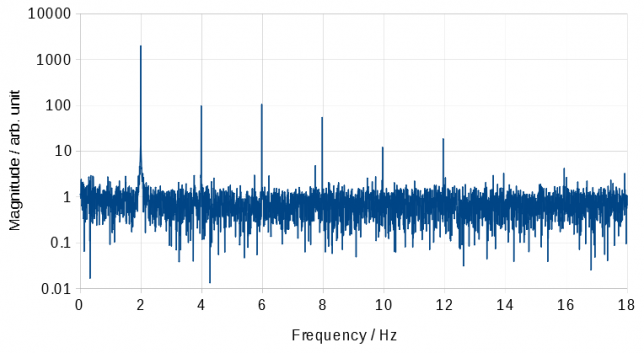
縦軸は対数スケールで表示しています．2.0 Hz 付近に最大のピークがありますが，それの高調波が少なくとも6次までははっきりと確認できます．

さて，もとの振動の周波数を求めるため，メインピークの周辺を拡大したものを Fig.4 に示します．メインピークの周波数は 1.991 Hz でした．横軸の刻みは 5 mHz ですが，両隣（1.986 Hz と 1.996 Hz）がほぼ同程度に落ち込んでいることから，実際の周波数は 1.991 Hz に近い（±1 mHz ぐらい？）ものと推測できます．

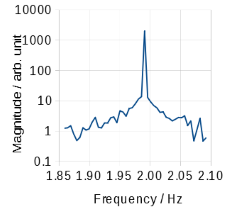
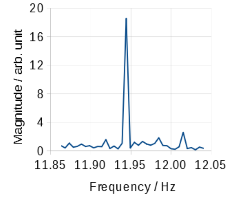
（そういうことが一般に行われるのかよくわかっていませんが）高調波のピークを見ると，周波数をより精密に求められる可能性があります．例えば6次の高調波のピーク周辺を拡大したものを Fig.5 に示します（縦軸は対数スケールではないので注意）．このピークは 11.944 Hz に位置していますので，もとの振動の周波数はこれを6で割った 1.9907 Hz になります．両隣の 1.9899 Hz や 1.9915 Hz（6で割った後の周波数で表示）ではほとんどバックグラウンドのレベルに落ちています．このことから，もとの振動の周波数は，1.9907 Hz に近い（±0.2 mHz ぐらい？）であると推測できます．