基礎物理学実験の題目「プリズム」では,ガラスの屈折率を最小偏角法で測定しています.最小偏角法の鍵となる最小偏角条件は,力任せに微分しても導出できるので,理科系大学生にとって微分積分学のちょうどいい演習問題だったりします.ここでは,凸関数という概念を用いて最小偏角条件をちょっとだけエレガントに導出する方法を思いついたので,それを公開してみます.
いくつかの書籍/Webサイトに目を通した限りでは,この方法で導出しているものは見つかりませんでした.そういうものを見つけましたら,こっそりお知らせ下さい.
■数学の準備
必要になる数学を振り返っておきましょう.いずれも大学の専門基礎レベルだと思います.
A.凸関数
凸関数の定義と,今回の導出で必要になる性質をまとめておきます.まず注意をいくつか述べますが,初めて読む人は気にする必要はありません.
- 凸関数というときは,いわゆる「下に凸」であるものだけを指します.「上に凸」なものは凹関数と呼ばれることが多いと思います.
- 凸関数の定義は(一次関数のように,凹な部分がなければよしとする)広義のものを採用することが多いのですが,ここでは狭義の定義を採用しています.
- ここでは関数の定義域全体で凸であるかどうかだけを考えます.定義域の一部において凸であるか否かを論じることも,世の中にはあります.
- ここでは引数が1次元の場合だけを考えます.
【定義】区間 ![]() を定義域とする実数値関数
を定義域とする実数値関数 ![]() について,
について,![]() が凸関数である ということを以下のように定義します.
が凸関数である ということを以下のように定義します.
![]() に属する相異なる2点
に属する相異なる2点 ![]() と,
と,![]() を満たす正の実数
を満たす正の実数 ![]() に対して,
に対して,
(1) ![]()
が成立する.
(1)式が一見ややこしいですが,グラフを考えると理解しやすいかもしれません.すなわち ![]() のグラフが,
のグラフが,![]() と
と ![]() の間では,線分
の間では,線分 ![]() よりも下にくるということです.
よりも下にくるということです.
なお凸関数であることをこの定義で示すのは一般に大変です. ![]() が2回微分可能であれば,次の定理で示すのが便利です.ここでは結論だけを述べます.証明は参考文献[1][2]などをご覧下さい.
が2回微分可能であれば,次の定理で示すのが便利です.ここでは結論だけを述べます.証明は参考文献[1][2]などをご覧下さい.
(2) ![]()
であれば,![]() は 凸関数である.「内点」というのは,区間
は 凸関数である.「内点」というのは,区間 ![]() のうちその両端以外の点,ぐらいに考えて構いません.
のうちその両端以外の点,ぐらいに考えて構いません.
B.逆正弦関数の微分
![]() の微分を確認しておきましょう(値域は,通常通り
の微分を確認しておきましょう(値域は,通常通り ![]() とします).
とします).
![]() より
より ![]() です.これと,逆関数の微分の公式を使います.
です.これと,逆関数の微分の公式を使います.
(3) 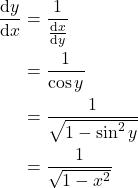
![]() の値域では
の値域では ![]() は負にならないので,平方根はプラスのものだけを考えれば十分ですね.
は負にならないので,平方根はプラスのものだけを考えれば十分ですね.
■最小偏角条件の導出
1.問題設定
ガラスと空気の境界で屈折が生じる場合,その「光線」の境界面法線に対する角度を,空気側とガラス側でそれぞれ ![]() とします.いわゆる入射角と屈折角です.ややこしい言い回しをしているのは,空気から入射する場合とガラスから入射する場合があるので,
とします.いわゆる入射角と屈折角です.ややこしい言い回しをしているのは,空気から入射する場合とガラスから入射する場合があるので,![]() が入射角の場合もあれば,
が入射角の場合もあれば,![]() が入射角の場合もあるからです.入射角(incidence)とは限らないのに
が入射角の場合もあるからです.入射角(incidence)とは限らないのに ![]() の文字を使うのは不自然ですが,本学の実験テキストに合わせて文字はそのままにしておきます.
の文字を使うのは不自然ですが,本学の実験テキストに合わせて文字はそのままにしておきます.
すると,当然ながら屈折の法則(スネルの法則)が成り立ちます.
(4) ![]()
![]() は空気に対するガラスの相対屈折率ですが,いまはそれを1より大きな一定値とします.するとしかるべき範囲の
は空気に対するガラスの相対屈折率ですが,いまはそれを1より大きな一定値とします.するとしかるべき範囲の ![]() に対して(ちゃんと書くと,0以上かつ臨界角以下の
に対して(ちゃんと書くと,0以上かつ臨界角以下の ![]() に対して)
に対して) ![]() が
が ![]() の関数であると見ることができます.
の関数であると見ることができます.
(5) ![]()
なお光線が三角柱プリズムを透過する際には,2つの面で屈折します.必要な場合は数字のインデックスで1回目の屈折と2回目の屈折を表します.
また幾何学的な条件により,![]() とプリズムの頂角
とプリズムの頂角 ![]() との間に次の関係があります.
との間に次の関係があります.
(6) ![]()
そして偏角 ![]() は次の式で与えられます.
は次の式で与えられます.
(7) ![]()
この ![]() が
が ![]() のときに最小となることを導きたい,というのが今回の問題です.
のときに最小となることを導きたい,というのが今回の問題です.
2.凸関数であることを認めて導出する
いま,(5)式の ![]() が凸関数であることを認めます.図1をご覧になれば,直感的には認めたくなるでしょう(数学的証明は次項で行います).
が凸関数であることを認めます.図1をご覧になれば,直感的には認めたくなるでしょう(数学的証明は次項で行います).
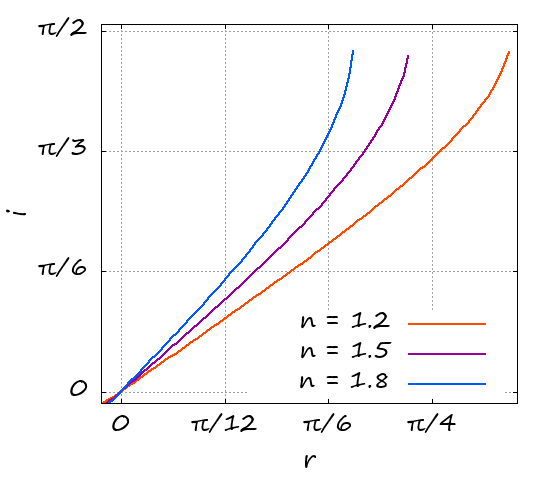
さて, ![]() を((6)式を満たすように)任意にとると,
を((6)式を満たすように)任意にとると, ![]() は以下の関係式を満たします.
は以下の関係式を満たします.
(8) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{align} \delta &= 2 \times [ \frac{1}{2} i(r_1) + \frac{1}{2} i(r_2) ] - \alpha \\ &\geqq 2 \times [ i(\frac{1}{2} r_1 + \frac{1}{2} r_2 ) ] - \alpha \\ &= 2 \times i(\frac{\alpha}{2}) - \alpha \\ &= 2 \times \sin^{-1}(n \cdot \sin ( \alpha / 2 ) ) - \alpha \end{align} \end{equation*}](https://home.hirosaki-u.ac.jp/yaneura/wp-content/ql-cache/quicklatex.com-ae17b3a59674c83591945c293ceb13f4_l3.png)
2行目の不等式は,(1)式で ![]() としたものですが,(8)式では等号を含むことに注意しましょう.(1)式では
としたものですが,(8)式では等号を含むことに注意しましょう.(1)式では ![]() でしたが,ここでは
でしたが,ここでは ![]() の場合も含むからです.すなわち(8)式の等号成立の必要十分条件が
の場合も含むからです.すなわち(8)式の等号成立の必要十分条件が ![]() であり,そのときに偏角
であり,そのときに偏角 ![]() が最小となることが示されました(ちなみに最小偏角は
が最小となることが示されました(ちなみに最小偏角は ![]() になります).
になります).
3.凸関数であることを示す
最後に (5)式の ![]() が凸関数であることを確認しましょう.そのためには,(2)式のような関係が
が凸関数であることを確認しましょう.そのためには,(2)式のような関係が ![]() について成り立つことを示せばいいのでした.そのまま微分すると表示が大変なので,
について成り立つことを示せばいいのでした.そのまま微分すると表示が大変なので,![]() を使って表示します.
を使って表示します.![]() ですね.ここでの
ですね.ここでの ![]() は
は ![]() であることにも注意しましょう.
であることにも注意しましょう.
(9) ![]()
![]() を残したままでもいいのですが,ここでは変数を
を残したままでもいいのですが,ここでは変数を ![]() だけにしました.
だけにしました.
(10) 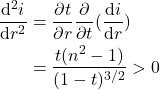
![]() かつ
かつ ![]() であったので,2行目の分子も分母も正になりますね.つまり2回微分が正になりましたので,
であったので,2行目の分子も分母も正になりますね.つまり2回微分が正になりましたので,![]() が凸関数であることが示されました.
が凸関数であることが示されました.
参考文献,Webサイト
凸関数に関して,以下の書籍等を参考にしました.
- 小平邦彦,解析入門(岩波基礎数学選書)
- WIIS,1変数の狭義凸関数・狭義凹関数
- 次ページの微分を用いた1変数の狭義凸関数・狭義凹関数の判定も合わせて参考にしました.