一様重力場中に一様な質量線密度のロープを両端を固定して垂らしたときにできる曲線がカテナリー曲線。懸垂曲線,懸垂線とも。 以下も参照:
以下も参照:
重力加速度 $g$ で表される一様重力場中に,両端を固定して垂らした一様な質量線密度 $\rho$ のロープ(ワイヤー,電線等なんでもよい)を考える。
水平方向を $x$,垂直方向を $y$,ロープ上の位置を $(x, y)$ として,まず,$y$ は以下の微分方程式
$$\frac{d^2 y}{dx^2} = a \sqrt{1 + \left( \frac{dy}{dx} \right)^2}$$
を満たすことを示す。ここで
$$a \equiv \frac{\rho g}{T_0}$$であり,$T_0$ は $\frac{dy}{dx} = 0$ の点におけるロープの張力である。
この方程式には名前がないようですが,カテナリー曲線をあらわす方程式ということで,カテナリー方程式とここでは呼ぶことにする。
カテナリー曲線は Wikipedia をはじめ多くのWebページにその説明がされているほどに有名であるが,他人の話を聞いても読んでもなかなか理解できない自分自身のために,自分が納得できるように,もう少しかみくだいて説明してみる。
カテナリー方程式の導出
ロープ素片にかかる力のつりあい
まず,ロープ上の点 $P(x, y(x))$ から $x’ \equiv x + dx$ として点 $Q(x’, y(x’))$ までの微小なロープ素片を考える。(図の赤い部分。この微小素片に働く力のつりあいを考えるところが私のちょっとしたこだわり。)
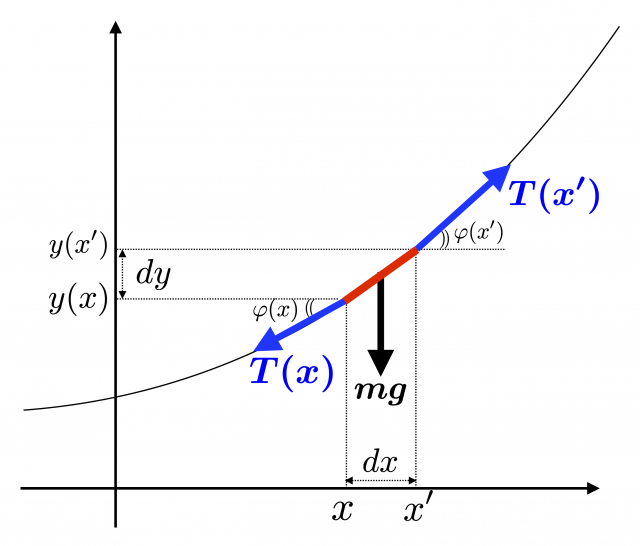
ロープの静止形状 $y(x)$ は,このロープ素片の一方の端にかかる張力 $T(x)$ と他方の端にかかる張力 $T(x’)$ およびロープ素片の質量を $m$ としたときの重力 $mg$ とのつりあいから求められる。
ロープ素片の傾き角 $\varphi(x)$ は
$$\tan \varphi(x) = \frac{dy}{dx} = y'(x)$$
で与えられる。
水平方向の力のつりあい
このロープ素片にはたらく力の水平方向のつりあいの式は
$$ T(x) \cos\varphi(x) = T(x’) \cos\varphi(x’) \tag{1}$$
これから直ちに
\begin{eqnarray}
\frac{d}{dx} \left( T(x) \cos\varphi(x) \right) &=& 0 \\
\therefore\ \ T(x) \cos\varphi(x) &=& \mbox{const.} \\
&\equiv& T_0
\end{eqnarray}
ここで $T_0$ は $\varphi = 0$ つまり $\frac{dy}{dx} = 0$ の点でのロープの張力である。
垂直方向の力のつりあい
垂直方向の力のつりあいの式は
$$ T(x) \sin\varphi(x) + mg = T(x’) \sin\varphi(x’) \tag{2}$$
ロープ素片の質量 $m$ は
\begin{eqnarray}
m &=& \rho \sqrt{dx^2 + dy^2} \\
&=& \rho \sqrt{1 + \left(\frac{dy}{dx}\right)^2} \ dx \\
&=& \rho \sqrt{1 + \tan^2 \varphi} \ dx \\
&=& \frac{\rho}{\cos\varphi(x)} \ dx
\end{eqnarray}
であるから,これを $(2)$ 式に代入して両辺に $\cos\varphi(x)$ をかけると
$${\color{blue}{T(x)\cos\varphi(x)}} \sin\varphi(x) + \rho g dx = T(x’) \sin\varphi(x’) \cos\varphi(x)$$
この式の左辺第1項に $(1)$ 式を代入して
$${\color{blue}{T(x’) \cos\varphi(x’)}}\sin\varphi(x) + \rho g dx = T(x’) \sin\varphi(x’) \cos\varphi(x)$$
\begin{eqnarray}
\therefore\ \ \rho g dx &=& T(x’) \sin\varphi(x’) \cos\varphi(x) – T(x’) \cos\varphi(x’)\sin\varphi(x) \\
&=& T(x’) \sin(\varphi(x’) – \varphi(x)) \\
&\simeq& \left(T(x) + \frac{dT}{dx} dx \right) \sin\left( \frac{d\varphi}{dx} dx \right) \\
&\simeq&T(x) \frac{d\varphi}{dx} dx \\ \ \\
\therefore\ \ \frac{d\varphi}{dx} &=& \frac{\rho g}{T(x)}
\end{eqnarray}
これを $y$ についての微分方程式にするために,$\frac{dy}{dx} = \tan\varphi$ の両辺を $x$ で微分する。
\begin{eqnarray}
\frac{dy}{dx} &=& \tan\varphi \\
\frac{d^2y}{dx^2} &=& \frac{d}{dx} \tan\varphi \\
&=& \frac{1}{\cos^2\varphi} \frac{d\varphi}{dx}\\
&=& \frac{1}{\cos^2\varphi}\frac{\rho g}{T(x)} \\
&=& \frac{\rho g}{T(x) \cos\varphi(x)} \frac{1}{\cos\varphi} \\
&=& \frac{\rho g}{T_0} \sqrt{1 + \tan^2\varphi}\\
&=& a \sqrt{1 + \left( \frac{dy}{dx}\right)^2}
\end{eqnarray}
となり,求められた。
カテナリー方程式の解
$$\frac{d^2 y}{dx^2} = a \sqrt{1 + \left( \frac{dy}{dx} \right)^2}$$
$\displaystyle \frac{dy}{dz} = z$ とおくと,変数分離できて「逆双曲線関数の微分」のページをみれば
$$ (\sinh^{-1} x)’ = \frac{1}{\sqrt{x^2 + 1}}$$
であったから,ただちに
\begin{eqnarray}
\frac{dz}{dx} &=& a \sqrt{1 + z^2} \\
\frac{dz}{\sqrt{1 + z^2}} &=& a \,dx \\
\int\frac{dz}{\sqrt{1 + z^2}} &=& \int a \,dx \\
\sinh^{-1} z &=& a x + C \\
\therefore\ \ z = \frac{dy}{dx} &=& \sinh(ax + C)
\end{eqnarray}
$x = 0$ で $\displaystyle y = h, \ \frac{dy}{dx} = 0$ という初期条件を課すと $C = 0$。
\begin{eqnarray}
\frac{dy}{dx} &=& \sinh(ax) \\
\therefore\ \ y &=& \int \sinh(ax) \, dx = \frac{1}{a} \cosh( ax ) + C
\end{eqnarray}
$x = 0$ で $y = h$ という初期条件より $C = h – \frac{1}{a}$
$$\therefore\ \ y = \frac{1}{a} \left( \cosh( ax ) -1 \right) + h$$
これが(定数部分をのぞけば $y = \frac{1}{a} \cosh (ax)$ が)カテナリー曲線である。
最下点近傍での近似表現
カテナリー曲線は,双曲線関数ハイパボリック・コサインであらわされ,放物線ではない。
ただし,ロープの質量線密度 $\rho$ が小さいとして $\rho$ したがって $a = \frac{\rho g}{T_0}$ の1次まで展開すると,
\begin{eqnarray}
y &=& \frac{1}{a} \left( \cosh( ax ) -1 \right) + h \\
&\simeq& \frac{1}{a} \left( 1 + \frac{a^2 x^2}{2} + \cdots -1\right) + h \\
&\simeq& h + \frac{1}{2} a x^2
\end{eqnarray}
となり,$\rho$ したがって $a = \frac{\rho g}{T_0}$ が小さいという状況(あるいは同等なことだが,最下点 $x = 0$ の近傍)では,カテナリー曲線は放物線として近似できることがわかる。
宇宙論にあらわれるカテナリー
「補足:スケール因子の解」のページで $\Omega_{\rm m} = 0, \ \Omega_{\Lambda} > 1$ (したがって $k > 0$)の場合に,スケール因子がハイパボリック・コサインを使って書かれることを示している。このようなふるまいをする宇宙を「カテナリー宇宙」と呼んでいるのであった。