太陽の表面すれすれをかすめてやってくる光は,太陽重力によってどれくらい曲げられるか?
衝突パラメータ $b$ を太陽半径 $R$ として光の「曲がり角」
$$\alpha = \frac{4 G M}{R c^2}$$ は角度にすれば何秒になるか。
Maxima-Jupyter での計算例
太陽の表面すれすれをかすめてやってくる光は,太陽重力によってどれくらい曲げられるか?
衝突パラメータ $b$ を太陽半径 $R$ として光の「曲がり角」
$$\alpha = \frac{4 G M}{R c^2}$$ は角度にすれば何秒になるか。
alpha = alpha: 4*G*M/(R * c**2);
/* 万有引力定数 */
G: 6.674E-11$
/* 太陽質量 */
M: 1.9891E30$
/* 太陽半径 */
R: 6.9551E8$
/* 光速 */
c: 299792458$
alpha = ev(alpha);
ラジアンを秒になおす。
fpprintprec: 3$
print(float(ev(alpha) /%pi * 180 * 60 * 60), "秒角")$
Python で光の曲がり角の計算
太陽の表面すれすれをかすめてやってくる光は,太陽重力によってどれくらい曲げられるか?衝突パラメータ $b$ を太陽半径 $R$ として光の「曲がり角」
$$\alpha = \frac{4GM}{c^2 R}$$
は角度にすれば何秒になるか。
モジュールの import
# 円周率とかを使いたいので
import numpy as np
# 万有引力定数
G = 6.674E-11
# 太陽質量
M = 1.9891E30
# 太陽半径
R = 6.9551E8
# 光速
c = 299792458
alpha = 4*G*M/(c**2 * R)
alpha
ラジアンを角度秒になおす。
print("α = %.2f 秒角" % (alpha/np.pi*180*60*60))
日食時の観測ではどこの角度を観測しているのか?
曲がり角 \(\alpha\) そのものは観測量ではない。(観測者のいる地点での量ではないから。)では,日食時の観測では,どの角度を観測して一般相対性論の予言と一致した!と言っているのであろうか?
考え方としては,以下の図のようになる。(角度は大げさになってます。)
まず,太陽重力による影響を受けない場合,遠方の星がある方向 \(P\) に見えたとする。
日食時は,太陽が遠方の星の手前に来て,本来ならば星からの光は遮られて見えないことになるが,太陽重力による光の曲がりによって,あたかも方向 \(\color{red}{Q}\) にあるように見える。
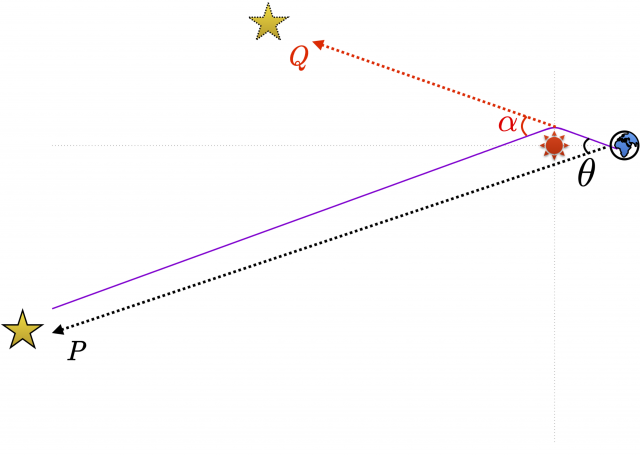
方向 \(P\) と方向 \(\color{red}{Q}\) の角度差 \(\theta\) が実際の観測から得られる角度である。上図のように,地球から太陽までの距離にくらべて,遠方の星が十分遠くにあれば,ほぼ(平行線の同位角は等しいということから)
$$\theta \simeq \color{red}{\alpha}$$
としてよい。したがって,一般相対論の予言である \(\color{red}{\alpha}\) の値を観測によって検証できることになる。