4元速度
慣性系 \(S\) (その座標を\(x^{\mu} = (t, x, y, z)\) とする)において,2人の観測者 \(A, B\) を考える。観測者 \(A\) は静止している基準観測者であり,観測者 \(B\) は \(A\) に対して\(+x\) 方向に速さ \(V\) で運動している。(以下,\(c = 1\))
\begin{eqnarray} ds^2 = – d\tau^2 &=& \eta_{\mu\nu} dx^{\mu} dx^{\nu} \\
&=& -dt^2 + dx^2 + dy^2 + dz^2 \end{eqnarray}
のように線素 \(ds^2\) から固有時間 \(\tau\) (の微小変位 \(d\tau\))を定義し,4元速度の成分を以下のように定義する。(\(\tau\) は世界線をパラメトライズするアフィンパラメータなのだが,その話はまたあとで… )
- 観測者 \(A\) の世界線を \(x^{\mu}(\tau)\), 世界線の接ベクトルである4元速度の成分を
$$ u^{\mu} = \frac{dx^{\mu}}{d\tau}$$ - 観測者 \(B\) の世界線を \(\bar{x}^{\mu}(\tau)\), 世界線の接ベクトルである4元速度の成分を
$$\bar{u}^{\mu} = \frac{d\bar{x}^{\mu}}{d\tau}$$
\(\bar{x}^{\mu}\) は別の慣性系での座標ではないことに注意。
慣性系はあくまで \(S\) のみ。全ての座標は \( x^{\mu} = (t,x,y,z) \) での値である。本来は観測者 \(A\) の世界線を \(x_A^{\mu}(\tau)\),観測者\(B\) の世界線を \(x_B^{\mu}(\tau)\) と書きたいところだが,そうすると4元速度の成分 \( u_B^{\mu} \) の下添字バージョンが \(u_{B\mu}\) などとなって目がチカチカしやすいので,苦渋の決断で,\(u_B^{\mu} \rightarrow \bar{u}^{\mu}\) と表記することにした。ご了承ください。
また,別セクション(「4次元時空のベクトル・線素・計量テンソル」の項)で説明するように,4元ベクトル \(\boldsymbol{u}\) の正式表記を成分 \(u^{\mu}\) と基本ベクトル \(\boldsymbol{e}_{\mu}\) を使って \( \boldsymbol{u} = u^{\mu} \boldsymbol{e}_{\mu}\) などと書くことになる。また,4元ベクトル同士の内積は \(\eta_{\mu\nu}\) で縮約をとることになる。
なので4元ベクトルといったら \(\boldsymbol{u}\) であり,\(u^{\mu}\) は4元ベクトルの成分,とできるかぎり言い分けることにする。
運動する観測者の4元速度
今,観測者 \(A\) は \(S\) 系では静止しているので,
\begin{eqnarray}
\frac{dx_A^i}{dt_A} \rightarrow \frac{dx^i}{dt} &=& \left( \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt} \right) \\
&=& \frac{u^i}{u^0} = (0, 0, 0)
\end{eqnarray}
また,4元速度 \(\boldsymbol{u}\)は,以下のように「大きさ」の2乗(自分自身との内積)が \(-1\) になっている。
\begin{eqnarray}
\boldsymbol{u}\cdot\boldsymbol{u} &=& \eta_{\mu\nu} u^{\mu} u^{\nu} \\
&=& \eta_{\mu\nu} \frac{dx^{\mu}}{d\tau} \frac{dx^{\nu}}{d\tau} \\
&=& \frac{\eta_{\mu\nu} dx^{\mu} dx^{\nu}}{d\tau^2} \\
&=& -1
\end{eqnarray}
このことから最終的に future-directed \(u^0 > 0\) を仮定して
$$ u^{\mu} = (1, 0, 0, 0) $$
一方,観測者 \(B\) は速さ\(V\) で \(+x\) 方向に運動しているので,
\begin{eqnarray}
\frac{dx_B^i}{dt_B} \rightarrow \frac{d\bar{x}^i}{d\bar{t}} &=& \left(\frac{d\bar{x}}{d\bar{t}}, \frac{d\bar{y}}{d\bar{t}}, \frac{d\bar{z}}{d\bar{t}}\right) \\
&=&\frac{\bar{u}^i}{\bar{u}^0} = (V, 0, 0)
\end{eqnarray}
規格化条件 \(\bar{\boldsymbol{u}}\cdot\bar{\boldsymbol{u}} = \eta_{\mu\nu} \bar{u}^{\mu} \bar{u}^{\nu} = -1 \) から最終的に
$$ \bar{u}^{\mu} = \left(\frac{1}{\sqrt{1-V^2}}, \frac{V}{\sqrt{1-V^2}}, 0, 0\right)$$
2人の観測者の4元速度の間の関係式
観測者 \(A\) からみた,観測者 \(B\) の空間的な運動方向を表す単位ベクトルを \(\boldsymbol{e}\),その成分を \(e^{\mu}\) とする。
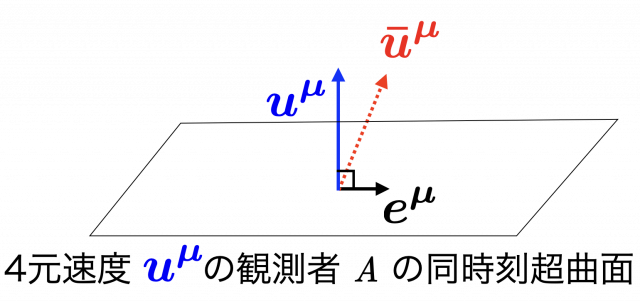
\(\boldsymbol{e}\) が空間的であるとは,観測者 \(A\) の4元速度 \(\boldsymbol{u}\) に直交することであり,
$$\boldsymbol{u}\cdot\boldsymbol{e} = \eta_{\mu\nu} u^{\mu} e^{\nu} = 0$$
また,単位ベクトルであるから,
$$\boldsymbol{e}\cdot\boldsymbol{e} = \eta_{\mu\nu}e^{\mu}e^{\nu} = 1$$
したがって,\(e^{\mu}\) は,\(u^{\mu} = (1, 0, 0, 0)\) である \(S\) 系では以下のように書ける。
$$ e^{\mu} = (0, 1, 0, 0)$$
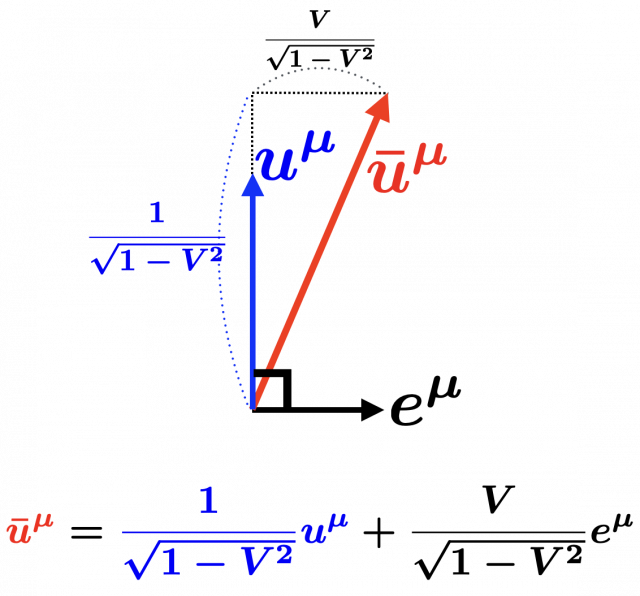
最終的に,観測者 \(B\) の4元速度 \(\bar{u}^{\mu} \) を,観測者 \(A\) の4元速度 \(u^{\mu} \) と,\(A\) に対する \(B\) の運動方向を表す \(e^{\mu}\) を使って,以下のように書けることがわかる。
\begin{eqnarray}
\bar{u}^{\mu} &=& \left(\frac{1}{\sqrt{1-V^2}}, \frac{V}{\sqrt{1-V^2}}, 0, 0\right) \\
&=& \frac{1}{\sqrt{1-V^2}} (1, 0, 0, 0) + \frac{V}{\sqrt{1-V^2}} (0, 1, 0, 0) \\
&=& \frac{1}{\sqrt{1-V^2}} u^{\mu} +\frac{V}{\sqrt{1-V^2}} e^{\mu}\\
\therefore \ \ \bar{\boldsymbol{u}} &=& \frac{1}{\sqrt{1-V^2}} \boldsymbol{u} +\frac{V}{\sqrt{1-V^2}} \boldsymbol{e}
\end{eqnarray}
4元速度の合成則
一旦ベクトル式で表された上の関係式は,座標系のとりかたによらずに成り立つ。従って,以下の表現が一般に成り立つ。これを(ガリレイ変換に基づく3次元速度の合成則との類似性から)4元速度の合成則と呼ぶことにしよう。(何か,もう少しいい名前があればいいのだが… )
$$ \bar{\boldsymbol{u}} = \frac{1}{\sqrt{1-V^2}} \boldsymbol{u} +\frac{V}{\sqrt{1-V^2}} \boldsymbol{e}$$
参考:ガリレイ変換に基づく3次元速度の合成則
参考までに,ニュートン力学において,ガリレイ変換に基づく速度の合成則をまとめておく。
4元ベクトルと区別するために,3次元ベクトルは \(\vec{v}\) のように \(\vec{\ }\) をつけて書くことにする。
速度 \(\vec{v}\) の物体に対して相対的に速度 \(\vec{V}\) (その大きさを \(V\),向きを表す単位ベクトルを \(\vec{e}\) とすると \(\vec{V} = V \vec{e}\))で運動する物体の速度 \(\vec{v}’\) は
$$\vec{v}’ = \vec{v} + \vec{V} = \vec{v} + V \vec{e}$$
これがガリレイ変換に基づく3次元速度の合成則である。
4元速度の合成則の逆変換
4元速度 \(\boldsymbol{u} \) の観測者 \(A\) に対して,\( \boldsymbol{u}\) に直交する空間的単位ベクトル \(\boldsymbol{e}\) の方向に3次元的な相対速度の大きさ \(V\) で運動する観測者 \(B\) の4元速度 \(\boldsymbol{u} \) は
$$ \bar{\boldsymbol{u}} = \frac{1}{\sqrt{1-V^2}} \boldsymbol{u} +\frac{V}{\sqrt{1-V^2}} \boldsymbol{e}$$
と書け,これを4元速度の合成則と呼ぶのであった。
一方,4元速度 \(\bar{\boldsymbol{u}}\) の観測者 \(B\) からみると,4元速度 \(\boldsymbol{u}\) の観測者 \(A\) は,\(\bar{\boldsymbol{u}}\) に直交する空間的単位ベクトル \(\bar{\boldsymbol{e}}\) のマイナス方向に3次元的な相対速度の大きさ \(V\) で運動しているようにみえる。したがって,
$$ \boldsymbol{u} = \frac{1}{\sqrt{1-V^2}} \bar{\boldsymbol{u}} -\frac{V}{\sqrt{1-V^2}}\bar{\boldsymbol{e}}$$
と書けるはずである。ここで,\(\bar{\boldsymbol{e}}\) は,\(\bar{\boldsymbol{u}} \) に直交する空間的単位ベクトルであることから
\begin{eqnarray}
\bar{\boldsymbol{u}}\cdot\bar{\boldsymbol{e}} &=& \eta_{\mu\nu} \bar{u}^{\mu}\bar{e}^{\nu} = 0\\
\bar{\boldsymbol{e}}\cdot\bar{\boldsymbol{e}} &=&\eta_{\mu\nu} \bar{e}^{\mu}\bar{e}^{\nu} = 1
\end{eqnarray}
上記の \(\bar{\boldsymbol{u}}= \cdots\) の式を \(\boldsymbol{u}= \cdots\) の式に代入して \(\bar{\boldsymbol{e}}\) について解くと,以下の式が導かれる。
$$\bar{\boldsymbol{e}}= \frac{1}{\sqrt{1-V^2}} \boldsymbol{e} + \frac{V}{\sqrt{1-V^2}} \boldsymbol{u}$$
同様に以下も導くことができる。
$$\boldsymbol{e}= \frac{1}{\sqrt{1-V^2}} \bar{\boldsymbol{e}} – \frac{V}{\sqrt{1-V^2}} \bar{\boldsymbol{u}}$$
まとめ
観測者 \(A\) の4元速度: \(\boldsymbol{u}\)
\(\boldsymbol{u}\) に直交する空間的単位ベクトル: \(\boldsymbol{e}\)
\begin{eqnarray}
{\boldsymbol{u}}\cdot{\boldsymbol{e}} &=& 0\\
{\boldsymbol{e}}\cdot{\boldsymbol{e}} &=& 1
\end{eqnarray}
観測者 \(A\) に対して,\(\boldsymbol{e}\) 方向に速さ \(V\) で運動する観測者 \(B\) の4元速度: \(\bar{\boldsymbol{u}}\)
\(\bar{\boldsymbol{u}}\) に直交する空間的単位ベクトル: \(\bar{\boldsymbol{e}}\)
\begin{eqnarray}
\bar{\boldsymbol{u}}\cdot\bar{\boldsymbol{e}} &=& 0\\
\bar{\boldsymbol{e}}\cdot\bar{\boldsymbol{e}} &=& 1
\end{eqnarray}
4元速度の合成則
\begin{eqnarray}
\bar{\boldsymbol{u}} &=& \frac{1}{\sqrt{1-V^2}} \boldsymbol{u} + \frac{V}{\sqrt{1-V^2}} \boldsymbol{e}\\
\bar{\boldsymbol{e}} &=& \frac{1}{\sqrt{1-V^2}} \boldsymbol{e} + \frac{V}{\sqrt{1-V^2}} \boldsymbol{u}
\end{eqnarray}
4元速度の合成則の逆変換
\begin{eqnarray}
\boldsymbol{u} &=& \frac{1}{\sqrt{1-V^2}} \bar{\boldsymbol{u}} – \frac{V}{\sqrt{1-V^2}} \bar{\boldsymbol{e}}\\
\boldsymbol{e} &=& \frac{1}{\sqrt{1-V^2}} \bar{\boldsymbol{e}} – \frac{V}{\sqrt{1-V^2}} \bar{\boldsymbol{u}}
\end{eqnarray}
以上の関係は,特殊相対論のみならず一般相対論においても成り立つ。これらは単に,時空の任意の1点における4元ベクトルの足し算引き算である。重力が存在する一般相対論的状況下においても,時空の任意の1点で,観測者 \(A\) の瞬間的共動座標系という局所慣性系をとることができ,そこでは特殊相対論における計算が成り立つからである。
ローレンツ因子
最後に一言。
4元速度の合成則およびその逆変換から,ただちに以下のことがわかる。
$$- \boldsymbol{u} \cdot\bar{\boldsymbol{u}} = \boldsymbol{e}\cdot \bar{\boldsymbol{e}} = \frac{1}{\sqrt{1-V^2}}$$
2つの4元速度同士,あるいはそれらに直交する2つの空間的単位ベクトル同士といった,4元ベクトル同士の内積がローレンツ因子 \( \displaystyle \frac{1}{\sqrt{1-V^2}}\) を与えることに注意。
ローレンツ因子は(4元ベクトルの内積からつくられる)4次元スカラー量であり,座標系の取り方によらない不変量である!というのがここでの立場である。
時間が遅れたり,棒が縮んたりするのも,すべてこの不変量であるローレンツ因子の影響である!
参考文献
G. F. R. Ellis – Relativistic Cosmology, in “General Relativity and Cosmology” ed. B. K. Sachs (Academic Press, New York, 1971) の P.147 の (6.11a) 式:
$$u_a = \cosh\beta\,u_a + \sinh\beta\, e_a, \quad e_a e^a = 1, \quad e^a u_a = 0 $$
とあり,その下に $V = \tanh \beta$ (原文では $V = \mbox{tgh}\ \beta$) と書いてある。これを膨らませて丁寧に書いてみると,上記のような説明になるかと。Ellis のこの式は,誤植なのか左辺と右辺に同じ $u_a$ があって,これなんのこと?と思って自分が納得できるようにかみくだいてみたのがこのページの内容。