光行差とは,光源に対する観測者の速度の違いによって,光の入射角が異なって観測される現象である。
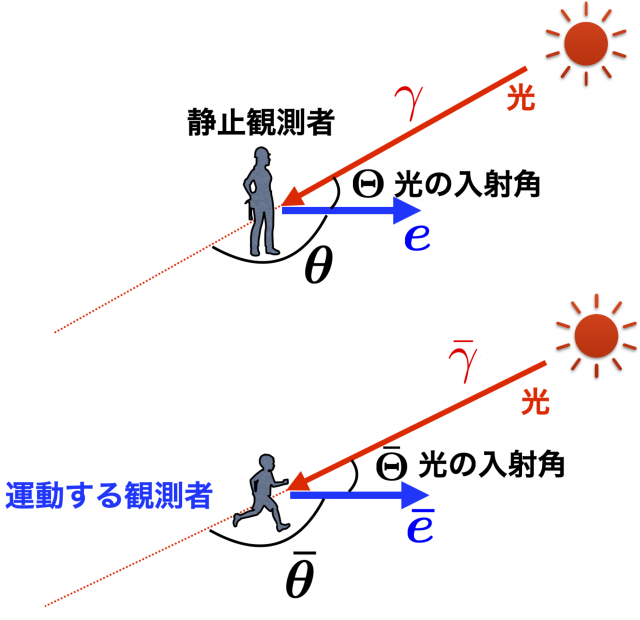
光の伝播を表す4元ベクトル \(\boldsymbol{k}\) は,振動数, 観測者 \(A, B\) の4元速度および光の伝播方向を表す空間的単位ベクトルを使って,以下のように書けるのであった。
$$ \boldsymbol{k} = \bar{\omega} (\bar{\boldsymbol{u}} + \bar{\boldsymbol{\gamma}})
= {\omega} ({\boldsymbol{u}} + {\boldsymbol{\gamma}})$$
$$\therefore \bar{\boldsymbol{u}} + \bar{\boldsymbol{\gamma}} = \frac{\omega}{\bar{\omega}} ({\boldsymbol{u}} + {\boldsymbol{\gamma}})$$
この式の両辺と \(\bar{\boldsymbol{e}}\) の内積をとると,左辺は
$$ \bar{\boldsymbol{e}}\cdot (\bar{\boldsymbol{u}} + \bar{\boldsymbol{\gamma}}) = \bar{\boldsymbol{e}}\cdot\bar{\boldsymbol{\gamma}} = \cos \bar{\theta}$$
一方,右辺は
\begin{eqnarray}
\color{red}{\frac{\omega}{\bar{\omega}}}
\color{blue}{\bar{\boldsymbol{e}}\cdot (\boldsymbol{u} + \boldsymbol{\gamma}) }
&=& \color{red}{\frac{\sqrt{1-V^2}}{1 – V\cos\theta}}
\color{blue}{\frac{1}{\sqrt{1-V^2}} (\boldsymbol{e} + V \boldsymbol{u}) \cdot(\boldsymbol{u} + \boldsymbol{\gamma})}\\
&=& \frac{1}{1 – V\cos\theta} (\boldsymbol{e}\cdot \boldsymbol{\gamma} + V \boldsymbol{u} \cdot \boldsymbol{u} ) \\
&=& \frac{\cos\theta -V}{1 – V\cos\theta}
\end{eqnarray}
$$\therefore \ \cos \bar{\theta} = \frac{\cos\theta -V}{1 – V\cos\theta}$$
2つの空間的単位ベクトルのなす角 \(\theta, \bar{\theta}\) を,光の入射角 \(\varTheta, \bar{\varTheta}\) を使ってあらわすと,\(\theta = \pi – \bar{\varTheta}, \ \bar{\theta} = \pi – \bar{\varTheta}\) であるから,
$$\cos (\pi – \bar{\varTheta}) = \frac{\cos(\pi – \varTheta) -V}{1 – V\cos(\pi – \varTheta)}$$
$$-\cos \bar{\varTheta} = \frac{-\cos\varTheta -V}{1 + V\cos\varTheta}$$
$$\therefore\ \cos \bar{\varTheta} = \frac{\cos\varTheta +V}{1 + V\cos\varTheta}$$
\(0 < \varTheta < \pi\) として \(\bar{\varTheta}\) と \(\varTheta\) の大小関係をみるために,引き算を行う。
\begin{eqnarray}
\cos \bar{\varTheta} – \cos\varTheta &=& \frac{\cos\varTheta +V – \cos\varTheta(1+V\cos\varTheta)}{1 + V\cos\varTheta} \\
&=& \frac{V \sin^2\varTheta}{1 +V\cos\varTheta} > 0
\end{eqnarray}
$$ \therefore \ \cos \bar{\varTheta} > \cos\varTheta$$
\(0 < \varTheta < \pi\) から入射する光については,コサインは単調減少関数なので,
$$ \bar{\varTheta} < \varTheta$$ 運動する観測者にとっては,光は進行方向に「寄って」くるように見える。たとえ静止観測者にとって光源が自身のまわり360度に均等に分布しているとしても,運動する観測者にとっては,その進行方向に光源が寄ってきて集中するように見える。これが(特殊相対論的効果としての)光行差である。