光のドップラー効果は,世にあまたある標準的な教科書では,ローレンツ変換を用いて説明されるのであった。ローレンツ変換にもとづいた光のドップラー効果の標準的な説明については,別ページ「光のドップラー効果のおさらい」にまとめてある。
ここでは,このセクションの方針「ローレンツ変換によらない特殊相対論の統一的理解」に則って,ローレンツ変換を使わずに光のドップラー効果の説明を試みる。
「光の4元ベクトル」のページで述べたように,光の伝播を表す4元ベクトル \(\boldsymbol{k}\) は,4元速度 \(\boldsymbol{u}\) の観測者 \(A\) が観測する振動数 \(\omega\) と光の伝播方向を表す空間的単位ベクトル \( \boldsymbol{\gamma}\) を使って,以下のように書けるのであった。$$ \boldsymbol{k} = \omega (\boldsymbol{u} + \boldsymbol{\gamma}), \quad\omega \equiv – \boldsymbol{k} \cdot\boldsymbol{u} $$
この同じ光,つまり同じ \(\boldsymbol{k}\) で表される光を,観測者 \(A\) に対して速度 \(V \boldsymbol{e} \) で運動する観測者 \(B\) が測定すると,その振動数 \(\bar{\omega}\) は,観測者 \(B\) の4元速度 \(\bar{\boldsymbol{u}}\) を使って以下のように書ける。$$ \bar{\omega} = – \boldsymbol{k}\cdot \bar{\boldsymbol{u}}$$
そして,
$$ \boldsymbol{k} = \bar{\omega} (\bar{\boldsymbol{u}} + \bar{\boldsymbol{\gamma}})$$
となり,\(\bar{\boldsymbol{\gamma}}\) は観測者 \(B\) が観測する光の進行方向を表す空間的単位ベクトルである。
$$ \bar{\boldsymbol{\gamma}}\cdot\bar{\boldsymbol{u}} = 0, \quad \bar{\boldsymbol{\gamma}}\cdot\bar{\boldsymbol{\gamma}} = 1$$
\(A\) とともに静止している光源からの光を運動する観測者 \(B\) が測定する場合
\(\bar{\omega}\) と \(\omega\) の関係は,以下のようにして求めることができる。
\begin{eqnarray}
\omega &=& – \boldsymbol{k}\cdot \boldsymbol{u} \\
&=& -\bar{\omega} (\bar{\boldsymbol{u}} + \bar{\boldsymbol{\gamma}})\cdot \frac{1}{\sqrt{1-V^2}} (\bar{\boldsymbol{u}} – V \bar{\boldsymbol{e}}) \\
&=& \bar{\omega} \frac{1+V \bar{\boldsymbol{\gamma}}\cdot \bar{\boldsymbol{e}}}{\sqrt{1-V^2}}\\
&=& \bar{\omega} \frac{1+V \cos\bar{\theta}}{\sqrt{1-V^2}}
\end{eqnarray}
ここで,\(\bar{\theta}\) は観測者 \(B\) が観測する,進行方向 \(\bar{\boldsymbol{e}}\) と光の空間的な進行方向 \(\bar{\boldsymbol{\gamma}}\) とのなす角であり,以下のように不変な4元スカラーとして定義される。
$$ \bar{\boldsymbol{\gamma}}\cdot \bar{\boldsymbol{e}} \equiv
\sqrt{\bar{\boldsymbol{\gamma}}\cdot\bar{\boldsymbol{\gamma}}}\sqrt{\bar{\boldsymbol{e}}\cdot\bar{\boldsymbol{e}}} \cos\bar{\theta} = \cos\bar{\theta}$$
$$ (\because \bar{\boldsymbol{\gamma}}\cdot\bar{\boldsymbol{\gamma}}= \bar{\boldsymbol{e}}\cdot\bar{\boldsymbol{e}} =1)$$
これは,2つの3次元ベクトル \(\vec{a}, \ \vec{b}\) の内積が,\(\vec{a}, \ \vec{b}\) のなす角 \(\theta\) を使って以下のように書けるということと全く同じ関係である。$$ \vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}| \cos\theta$$
したがって,あらためて光源静止系での振動数 \(\omega\) を \(\omega_0\) ,運動する観測者が測定する振動数 \( \bar{\omega}\) を \(\omega_{\rm obs}\) と表記し直すと
$$\omega_{\rm obs} = \omega_0 \frac{\sqrt{1-V^2}}{1+V \cos\bar{\theta}}$$
観測者 \(B\) が光源から遠ざかる場合
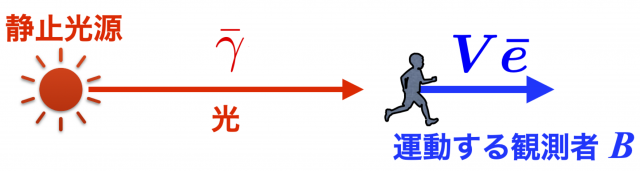
\(\bar{\boldsymbol{\gamma}}\) と \(\bar{\boldsymbol{e}}\) は同じ向きなので \(\bar{\theta} = 0\),従って \(\cos\bar{\theta} = 1\) となり,$$ \omega_{\rm obs}= \omega_0 \frac{\sqrt{1-V^2}}{1+V } = \omega_0 \sqrt{\frac{1-V}{1+V} }< \omega_0 $$
光源から遠ざかる観測者が測定する振動数は,光源静止観測者のそれよりも小さくなる。振動数が下がる,すなわち波長が伸びる。
観測者 \(B\) が光源に近づく場合
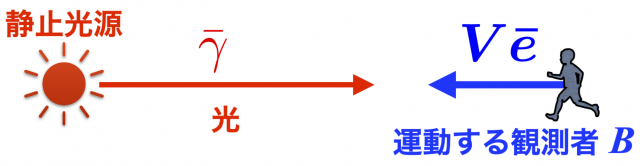
\(\bar{\boldsymbol{\gamma}}\) と \(\bar{\boldsymbol{e}}\) は反対向きなので \(\bar{\theta} = \pi\),従って \(\cos\bar{\theta} = -1\) となり,$$ \omega_{\rm obs} = \omega _0 \frac{\sqrt{1-V^2}}{1-V } = \omega_0 \sqrt{\frac{1+V}{1-V} }> \omega_0 $$
光源に近づく観測者が測定する振動数は,光源静止観測者のそれよりも大きくなる。振動数が上がる,すなわち波長が短くなる。
横ドップラー効果

\(\bar{\boldsymbol{\gamma}}\) と \(\bar{\boldsymbol{e}}\) が直交する場合,\(\bar{\theta}=\pi/2\),従って\(\cos\bar{\theta} = 0\) となり,$$ \omega_{\rm obs} = \omega_0 {\sqrt{1-V^2}} < \omega_0$$ 光源に対する観測者 \(B\) の相対速度はこの瞬間ゼロ(すなわち光源に向かうあるいは離れる速度成分はゼロ)であるが,振動数の変化が起こる。特殊相対論特有のこの現象は特に「横ドップラー効果」と呼ばれる。
\(B\) とともに運動している光源からの光を静止観測者 \(A\) が測定する場合
\(\bar{\omega}\) と \(\omega\) の関係は,以下のようにして求めることができる。
\begin{eqnarray}
\bar{\omega} &=& – \boldsymbol{k} \cdot\bar{\boldsymbol{u}} \\
&=& -\omega (\boldsymbol{u} + \boldsymbol{\gamma})\cdot \frac{1}{\sqrt{1-V^2}} (\boldsymbol{u} + V \boldsymbol{e}) \\
&=& \omega\frac{1-V \boldsymbol{\gamma}\cdot\boldsymbol{e}}{\sqrt{1-V^2}}\\
&=& \omega \frac{1-V \cos\theta}{\sqrt{1-V^2}}
\end{eqnarray}
ここで,\(\theta\) は観測者 \(A\) が測定する光源の進行方向 \(\boldsymbol{e}\) と光の空間的な進行方向 \(\boldsymbol{\gamma}\) とのなす角である。したがって,あらためて光源静止系での振動数 \(\bar{\omega}\) を \(\omega_0\) ,観測者 \(A\) が測定する振動数 \( \omega\) を \(\omega_{\rm obs}\) と表記し直すと
$$\omega_{\rm obs} = \omega_0 \frac{\sqrt{1-V^2}}{1-V \cos\theta}$$
光源が観測者 \(A\) から遠ざかる場合
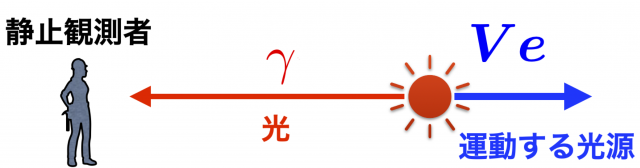
\(\boldsymbol{e}\) と \(\boldsymbol{\gamma}\) は反対向きなので,\(\theta=\pi\),したがって \(\cos\theta = -1\) となり,
$$\omega_{\rm obs} = \omega_0 \frac{\sqrt{1-V^2}}{1+V } = \omega_0 \sqrt{\frac{1-V}{1+V}} < \omega_0$$
光源が観測者 \(A\) に近づく場合

\(\boldsymbol{e}\) と \(\boldsymbol{\gamma}\) は同じ向きなので,\(\theta=0\),したがって \(\cos\theta = 1\) となり,
$$\omega_{\rm obs} = \omega_0 \frac{\sqrt{1-V^2}}{1-V } = \omega_0 \sqrt{\frac{1+V}{1-V}} > \omega_0$$
横ドップラー効果
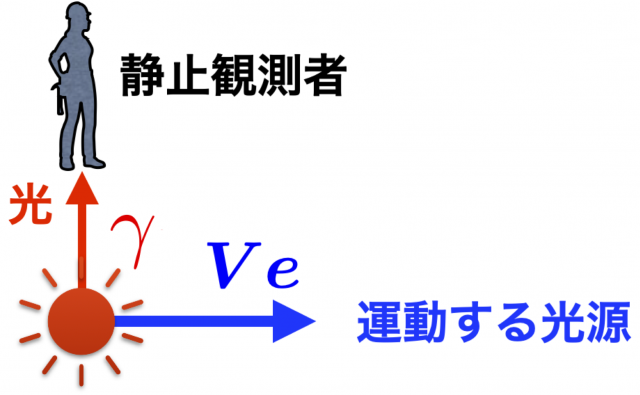
\(\boldsymbol{e}\) と \(\boldsymbol{\gamma}\) が直交する場合,\(\theta=\pi/2\),したがって \(\cos\theta=0\) となり,
$$\omega_{\rm obs} = \omega_0\sqrt{1-V^2} < \omega_0$$
観測者 \(A\) に対する光源の相対速度はこの瞬間ゼロ(すなわち,観測者へ向かうあるいは離れる速度成分はゼロ)であるが,振動数の変化が起こる。特殊相対論特有のこの現象は特に「横ドップラー効果」と呼ばれる。
補足:ドップラー効果は相対速度のみで決まるか?
以上のことから,光のドップラー効果は光源が動くか,観測者が動くかが問題になるのではなく,光源と観測者間の相対速度 \(V\) のみによって決まることがわかる。
Wikipedia のドップラー効果の項でも,ドップラー効果は「波(音波や電磁波など)の発生源(音源・光源など)と観測者との相対的な速度の存在によって、波の周波数が異なって観測される現象」であると説明されている。
しかし,これは光については本稿で述べたように当てはまるが,音については当てはまらない。同じ速さ \(v\) であっても,音源が動くのか,観測者が動くのかで答えは異なることに注意。したがって「相対速度」だけで決まるのではない。以下の Memo も参照。
追記:横ドップラー効果について補足
上で述べたように,静止観測者 \(A\) に対する運動光源の相対速度がゼロ,または静止光源に対する運動観測者 \(B\) の相対速度がゼロの瞬間であっても,振動数の変化が起こり,特殊相対論特有のこの現象は特に「横ドップラー効果」と呼ばれるのであったが,思うところあって,以下のようなページも追加して書いてみたので,参考までに。
はじめは,相対速度がゼロの瞬間に「横ドップラー効果」として観測された光は,いつ発射された光なのか,ひょっとして(たぶん)相対速度がある時に発射された光でしょ?という疑いで調べてみたのが,「光行差」という現象も考える必要があるよね,という話になった。