授業の定積分のところで，グラフを描いてから面積や体積を求めるように学生さんに言ったので。
曲線で囲まれた領域の面積
次の図形の面積を求めなさい。
$\ \ $放物線 $y = (x-2)^2$ と，$x$ 軸 ($y = 0$)，$y$ 軸とで囲まれた図形
曲線のグラフを描く
まずグラフを描きます。
関数 $y = f(x) = (x-2)^2$ と $x$ 軸 $y = g(x) = 0$ で囲まれているので，上下の線を一緒に図示してみます。
f(x):= (x - 2)**2;
g(x):= 0;
plot2d([f(x), g(x)], [x, -0.2, 2.2],
[legend, "(x-2)^2", ""])$
領域を縁取る
グラフの描画範囲と，横軸縦軸の表示範囲を別々に設定するために，媒介変数表示でグラフを描きます。
$x = x(t), y = y(t)$ を $a \leq t \leq b$ の範囲でグラフを描く例：
plot2d([parametric, x(t), y(t), [t, a, b])$
以下は，3本のグラフを一緒に描く例。いくつかオプションも設定。
plot2d([[parametric, t, f(t), [t, 0, 2]], /* y = f(x) */
[parametric, t, g(t), [t, 0, 2]], /* x 軸 y = g(x) */
[parametric, 0, t, [t, 0, 4]] /* y 軸 */
],
/* 線の色や太さの設定 */
[color, blue, black, black],
[style, [lines, 2], [lines, 2], [lines, 2]],
/* 横軸縦軸の表示範囲 */
[x, -0.5, 2.5], [y, -0.5, 4.5],
/* 凡例の設定 */
[legend, "(x-2)^2", "", ""])$
面積を求める
求める面積は…
'integrate(f(x) - g(x), x, 0, 2) =
integrate(f(x) - g(x), x, 0, 2);
領域を塗りつぶす
$0 < x < 2$ の範囲で，$y = (x-2)^2$ と $y = 0$ で囲まれた部分を黄色で塗りつぶす例。Maxima では plot2d() ではなく，draw2d() 関数を使います。以下の例を参照。
/* 囲まれた部分を塗りつぶして表示。*/
draw2d(/* 塗りつぶす色の指定。*/
fill_color = yellow,
/* 上の線。y = f(x) を filled_func に代入。*/
filled_func = f(x),
/* 下の線。y = g(x) を 0 < x < 2 の範囲で描く。*/
explicit(g(x), x, 0, 2))$
/* もう少しオプションを付けて。*/
/* 縦の線 x = 0 も描いてみる。 */
draw2d(/* x 軸 y 軸の表示範囲の設定。*/
xrange = [-0.5, 2.5], xaxis=true,
yrange = [-0.5, 4.5], yaxis=true,
/* 塗りつぶす色の指定。*/
fill_color = yellow,
/* 上の線。y = f(x) を filled_func に代入。*/
filled_func = f(x),
/* 下の線。y = g(x) を 0 < x < 2 の範囲で描く。*/
explicit(g(x), x, 0, 2),
/* 追加の線は parametric で描く。 */
/* x = x(t), y = y(t), a < t < b のグラフは */
/* parametric(x(t), y(t), t, a, b) と書く。 */
/* 線の太さを 2 にしてメリハリをつけて */
line_width = 2, nticks = 200,
/* 上の線。y = f(x) */
color = blue, key = "(x-2)^2",
parametric(t, f(t), t, 0, 2),
/* 下の線。y = g(x) */
color = black, key = "",
parametric(t, g(x), t, 0, 2),
/* x = 0 (y 軸) */
color = black, key = "",
parametric(0, t, t, 0, 4)
)$
回転体の体積
次の図形を $x$ 軸のまわりに1回転させてできる回転体の体積 $V$ を求めなさい。
曲線 $y = \sqrt{x}$ と $x$ 軸，直線 $x = 1$ で囲まれた図形
曲線のグラフを描く
まず，グラフを描きます。
f(x):= sqrt(x);
plot2d(f(x), [x, 0, 1])$
回転させる領域を縁取る
グラフの描画範囲と，縦軸横軸の表示範囲を別途設定したい場合は，媒介変数表示 parametric で表示するとよい。
$x = x(t), y = y(t)$ を $a \leq t \leq b$ の範囲で描く例：
plot2d([parametric, x(t), y(t), [t, a, b]])$
plot2d([[parametric, t, f(t), [t, 0, 1]], /* y = f(x) */
[parametric, t, 0, [t, 0, 1]], /* x 軸 y = 0 */
[parametric, 1, t, [t, 0, 1]]], /* x = 1*/
/* 線の色や太さの設定 */
[color, blue, black, black],
[style, [lines, 2], [lines, 1], [lines, 1]],
[x, -0.5, 1.5], [y, -1.5, 1.5],
[legend, "sqrt(x)", "", ""])$
体積を求める
回転体の体積は $\displaystyle V = \int_a^b \pi \left\{f(x)\right\}^2 \, dx$ であった。
V = integrate(%pi * f(x)**2, x, 0, 1);
回転させる領域を塗りつぶす
draw2d(/* x 軸 y 軸の表示範囲の設定。*/
xrange = [-0.2, 1.5],
yrange = [-1.5, 1.5],
xaxis = true,
/* 塗りつぶす色の指定。*/
fill_color = yellow,
/* 上の線。y = f(x) を filled_func に代入。*/
filled_func = f(x),
/* 下の線。y = 0 （x軸）を 0<x<1 の範囲で描く。*/
explicit(0, x, 0, 1),
/* 追加の線は parametric で描く。 */
/* x = x(t), y = y(t), a < t < b のグラフは */
/* parametric(x(t), y(t), t, a, b) とする。*/
/* 線の太さを 2 にしてメリハリをつけて */
nticks = 500, line_width = 2,
/* y = f(x) */
color = blue, key = "sqrt(x)",
parametric(t, f(t), t, 0, 1),
/* y = -f(x) */
color = blue, key = "",
parametric(t, -f(t), t, 0, 1),
/* 回転体の底面を楕円で描く。*/
color = blue, key = "",
parametric(0.1*cos(t)+1, 1*sin(t), t, 0, 2*%pi)
)$
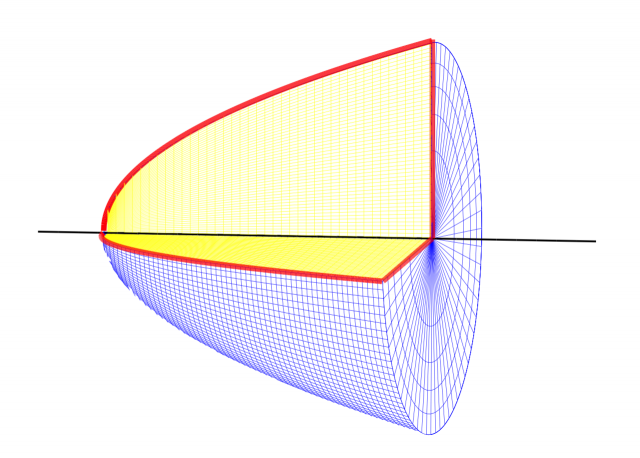
回転体をそれらしく3次元的に描く
もう少し3次元的なグラフにしてみます。
$y = f(x)$ を $x$ 軸のまわりに角度 $\theta$ したときにできる曲面上の点 $P$ の座標は
\begin{eqnarray}
x &=& x\\
y &=& f(x) \cos\theta \\
z &=& f(x) \sin\theta
\end{eqnarray}
です。この曲面を plot3d() 関数で描きます。
plot3d(/* 媒介変数表示の曲面を描く。*/
[x, f(x)*cos(t), f(x)*sin(t)],
[x, 0, 1], [t, 0, 2*%pi],
/* 各種設定。*/
[xtics, false], [ytics, false], [ztics, false],
[x, -0.2, 1.5], [y, -1.2, 1.2], [z, -1.2, 1.2],
[elevation,85], [azimuth,5], [grid, 60,36],
[legend, ""]
)$
このままだと底面が描かれておらず，なんとなく底が抜けている感じです。 plot3d() では，どうすれば媒介変数表示の曲面を複数描くことができるか，今のところ不明です。
draw3d() を使うと，もう少し柔軟に描けそうです。以下の例を参照。
draw3d(
xrange = [-0.2, 1.5],
yrange = [-1.5, 1.5],
zrange = [-1.1, 1.1],
/* 側面 */
line_width=0.2, xu_grid = 60, yv_grid = 36,
parametric_surface(x, f(x)*cos(t), f(x)*sin(t),
x, 0, 1, t, 0, 2*%pi),
/* 底面 */
xu_grid = 6, yv_grid = 36,
parametric_surface(f(1), x*cos(t), x*sin(t),
x, 0, 1, t, 0, 2*%pi),
/* 諸設定*/
surface_hide =true, view=[90, 9],
axis_3d = false,
/* x 軸 */
color=black, line_width = 1,
parametric(x, 0, 0, x, -0.2, 1.5),
/* z = f(x) を隠れないように少しずらして */
nticks=1000, color=red, line_width = 2,
parametric(x, 0, sqrt(x)+0.01, x, 0, 1),
parametric(1, 0.01, x, x, 0, 1+0.01)
)$
回転体の「切り口」を見せる例
Maxima の draw3d() だけで作ってみました。（svg ファイルが巨大になったので png に変換。）
