何度も言うが,光の経路は測地線であり,接ベクトルが経路に沿って一定であり続ける「まっすぐな」線である。
$$\frac{d\boldsymbol{k}}{dv} = \boldsymbol{0}$$
ではなぜ,「重力によって光さえも曲がる」などと言うのか,について補足する。
\(r_g \) のゼロ次解が直線であること
\(r_g\) のゼロ次解は
$$u = \frac{1}{r} = \frac{\sin\phi}{b}$$
\(r \rightarrow \infty\) での漸近的な振る舞いをみると,\(\displaystyle \frac{1}{r} \rightarrow 0 \) となることから \(\sin\phi = 0\) より \(\phi = 0, \ \pi\)。
つまり光は \(\phi = 0\) の無限遠からやってきて,\(\phi = \pi\) の無限遠へ去っていく。角度差は \(\pi – 0 = \pi\),つまり漸近的無限遠での振る舞いから経路は直線である,と結論づけることができる。
あるいは,極座標からデカルト座標へ変換すると,
$$ y = r \sin\theta \sin\phi = \frac{b}{\sin\phi} \sin\frac{\pi}{2} \sin\phi = b = \mbox{const.}$$
つまり,\( y = b \) という \(x\) 軸に平行な直線を表していることがわかる。
\(b\) はこの直線と座標原点(にこれから置かれるであろう天体)との最短距離を表し,衝突パラメータと呼ばれる。原点のどれだけ近くをかすめていくのかという,すれすれ度合いをあらわす。
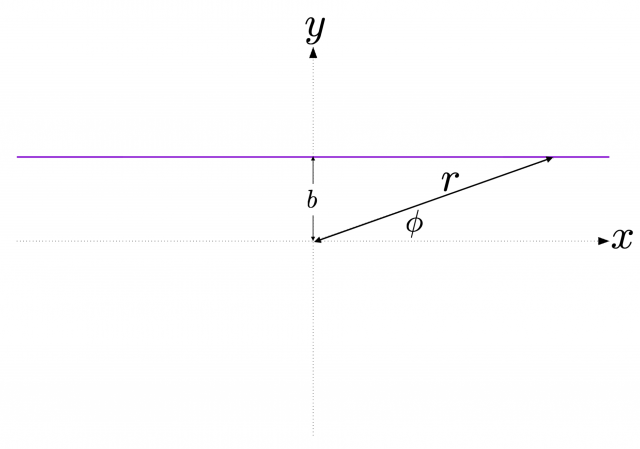
\(r_g\) の1次の効果を取り入れた解の漸近的振る舞い
\(r_g\) の1次の効果を取り入れた解
$$ \frac{1}{r} = \frac{\sin\phi}{b} + \frac{r_g}{2 b^2} \left(2 -\sin\phi -\sin^2\phi\right)$$ について,\( r \rightarrow \infty\) となるのは
$$ \sin\phi + \frac{r_g}{2 b} \left(2 -\sin\phi -\sin^2\phi\right) = 0 $$ のとき。
$r_g$ のゼロ次解は $\sin\phi = 0$ であるから,$\sin\phi$ は $O(r_g)$ であり,$r_g$ の1次までの近似で
$$ \sin\phi \simeq – \frac{r_g}{b} $$
のように解ける。
\( |\phi| \ll 1 \) については \(\sin\phi \simeq \phi \) であるから,\(\displaystyle \frac{r_g}{b} \ll 1 \) であれば,つまり光の漸近的無限遠での振る舞いをみると \(\displaystyle \phi = -\frac{r_g}{b} \) だけ傾いた漸近線に並行な無限遠からやってきて,\(\displaystyle \phi = \pi + \frac{r_g}{b} \) だけ傾いた漸近線に並行な無限遠に去っていく。
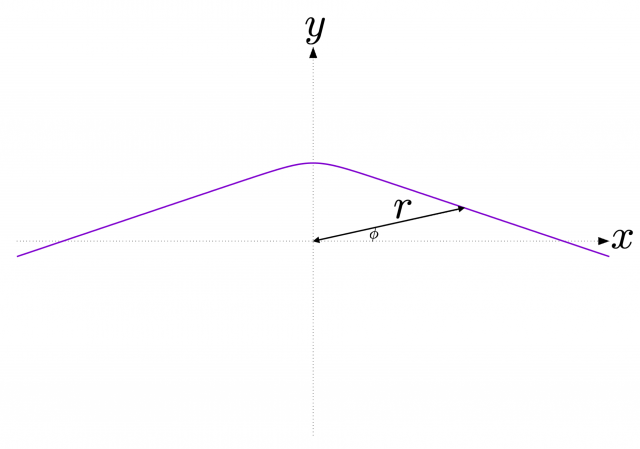
漸近的平坦性を仮定した光の「曲がり角」の定義
無限遠での漸近線の角度差は
$$ \pi + \frac{r_g}{b} – \left( -\frac{r_g}{b}\right) = \pi + 2\frac{r_g}{b}$$
つまり,直線から \(\displaystyle \alpha \equiv \frac{2 r_g}{b}\) だけ曲がっていることになる。この \(\alpha\) を光の「曲がり角」という。
\(r \rightarrow \infty \) ではシュバルツシルト時空はほぼ平坦
$$ds^2 \simeq -c^2 dt^2 + dr^2 + r^2 (d\theta^2 + \sin^2\theta\,d\phi^2)$$となるので,このような漸近的無限遠における漸近的平坦時空では角度座標 \(\phi\) が実際の角度をあらわしているとして問題ない。
ということで,世に数多ある教科書に書かれている説明では,漸近的平坦性を仮定し,光の経路の漸近的無限遠での漸近線の傾きをもって光の経路の角度とし,漸近線の傾きの差をもって光の「曲がり角」と定義している。
漸近的平坦性を仮定しない不変的な角度の定義
一般の時空内の任意の点における3次元的な角度の不変な定義についてまとめる。以下では,具体的な計算の際にはシュバルツシルト時空の計量テンソルの成分等を使っているが,定義自体は座標系によらない不変的な定義であり,任意の時空で使える。
空間的ベクトルの内積から定義される角度
一般に,観測者の4元速度 \(\boldsymbol{u}\) に直交する空間的単位ベクトルを \(\boldsymbol{n}, \ \boldsymbol{\gamma}\) とすると,
$$\boldsymbol{n}\cdot\boldsymbol{u} = 0, \ \boldsymbol{\gamma}\cdot\boldsymbol{u} = 0, \ \boldsymbol{n}\cdot\boldsymbol{n} = 1, \ \boldsymbol{\gamma}\cdot\boldsymbol{\gamma} = 1$$
この2つの空間的単位ベクトル \(\boldsymbol{\gamma}, \ \boldsymbol{n}\) のなす角を \(\varPsi\) は,以下の式から求めることができる。
$$\cos\varPsi \equiv \boldsymbol{\gamma}\cdot\boldsymbol{n}$$
4元ベクトル同士の内積から定義された \(\cos\varPsi\) したがって \(\varPsi\) は4次元スカラーであり,座標系によらない不変量である。
静止観測者の4元速度
まず,シュバルツシルト時空中の静止観測者の4元速度 \(\boldsymbol{u}\) の成分 \(u^{\mu}\) は
$$ u^{\mu} = \left(\frac{1}{\sqrt{1-\frac{r_g}{r}}}, 0, 0, 0\right)$$
\(\boldsymbol{u}\) に直交する同時的3次元空間への射影演算子 \(P^{\mu}_{\ \ \ \nu}\) は
$$P_{\mu \nu} = g_{\mu\nu} + u_{\mu} u_{\nu}$$
動径方向の単位ベクトル
さて,\(\boldsymbol{n}\) をこの3次元空間における動径方向(中心向き)の単位ベクトル,その成分を \(n^{\mu}\) とすると,空間成分は動径成分のみであることから \(n^2 = n^3 = 0\)。また,\(\boldsymbol{u}\) に直交すること \( \boldsymbol{u}\cdot\boldsymbol{n} = u_{\mu} n^{\mu} = u_0 n^0 = 0 \) より \(n^0 = 0\),さらに規格化条件条件 \(\boldsymbol{n}\cdot\boldsymbol{n} = 1\) より最終的に
$$ n^{\mu} =\left( 0, – \sqrt{1-\frac{r_g}{r}}, 0, 0\right)$$
光の進む向きを表す単位ベクトル
\(\boldsymbol{\gamma}\) を \(\boldsymbol{k}\) で表される光の進む向きを表す空間的単位ベクトルとすると,その成分は
$$ \gamma_{\mu} \equiv \frac{P_{\mu\nu} k^{\nu}}{\omega}$$ となる。ここで \(\omega \) は4元速度 \(\boldsymbol{u}\) の観測者が観測する光の振動数をあらわし,シュバルツシルト時空では
\begin{eqnarray}
\omega = – \boldsymbol{k}\cdot\boldsymbol{u} &=& -k_0\, u^0 \\
&=& \frac{\omega_c}{\sqrt{1-\frac{r_g}{r}}}
\end{eqnarray}
これから \(\boldsymbol{\gamma}\) の成分 \(\gamma_{\mu} = g_{\mu\nu} \gamma^{\nu}\) のうち,実際に計算に使う \(\gamma_1\) は
\begin{eqnarray}
\gamma_1 &=& \frac{1}{\omega} P_{1\mu} k^{\mu} \\
&=& \frac{1}{\omega} g_{11} k^1 \\
&=& \frac{1}{\omega} g_{11} \frac{dr}{d\phi} \frac{d\phi}{dv} \\
&=& \frac{\sqrt{1-\frac{r_g}{r}}}{\omega_c} \frac{1}{1-\frac{r_g}{r}} \frac{\ell}{r^2} \frac{dr}{d\phi} \\
&=& \frac{\ell}{\omega_c} \frac{-1}{\sqrt{1-\frac{r_g}{r}}} \frac{d}{d\phi}\left(\frac{1}{r}\right)
\end{eqnarray}
となる。
内積で定義される角度
2つの空間的単位ベクトル \(\boldsymbol{n}\) と \(\boldsymbol{\gamma}\) のなす角 \(\varPsi\) は,光の伝播方向と動径方向のとのなす角であり,その \(\cos\) は以下の式から求められる。
$$ \cos\varPsi \equiv \boldsymbol{\gamma}\cdot\boldsymbol{n} = \gamma_1 n^1 =\frac{\ell}{\omega_c} \frac{d}{d\phi}\left(\frac{1}{r}\right)$$
この角度 \(\varPsi\) が,シュバルツシルト時空の赤道面上(\(\theta = \pi/2\))の任意の点 \(\displaystyle \left( r(\phi), \phi\right)\) における光が動径方向となす角である。4元ベクトルの内積で定義される \(\varPsi\) は4元スカラーであり,座標系によらない不変量である。
ここに,\(r_g\) の1次までの解
$$\frac{1}{r} = \frac{\sin\phi}{b} + \frac{r_g}{2 b^2} \left(2 -\sin\phi -\sin^2\phi\right)$$ をいれると
\begin{eqnarray}
\cos\varPsi &=& \left( \frac{1}{b^2} -\frac{r_g}{b^3}\right)^{-\frac{1}{2}} \,
\frac{\cos\phi}{b}\, \left\{1 -\frac{r_g}{2 b} (1 + 2 \sin\phi) \right\} \\
&\simeq& \cos\phi\, \left( 1 -\frac{r_g}{b} \sin\phi\right)
\end{eqnarray}
となる。これから \(\sin\varPsi\) を求めると,
\begin{eqnarray}
\sin\varPsi &=& \sqrt{1 – \cos^2\varPsi} \\
&\simeq& \sqrt{1 – \cos^2\phi \left( 1 – 2 \frac{r_g}{b} \sin\phi \right) } \\
&=& \sin\phi \sqrt{ 1 + 2\frac{r_g}{b} \frac{\cos^2\phi}{\sin\phi} }\\
&\simeq& \sin\phi + \frac{r_g}{b} \cos^2\phi
\end{eqnarray}
光が $x$ 軸と交わる角度と「曲がり角」
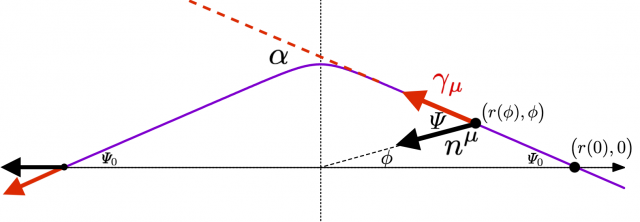
光は \(\phi = 0\) で \(x\) 軸と交わる。そのときの角度 \(\varPsi\) を \(\varPsi_0\) とすると,
$$\sin\varPsi_0 = \sin 0 + \frac{r_g}{b} \cos^2 0 = \frac{r_g}{b}$$
\(|\varPsi_0 | \ll 1 \) であるから
$$\varPsi_0 \simeq \frac{r_g}{b}$$ \(\phi = \pi\) で \(x\) 軸と交わるときの角度も同じである。
ここまでの角度は,シュバルツシルト時空中での \(r_g\) の1次までの精度で求めた(くどいようだが)現実の曲がった時空での角度である。
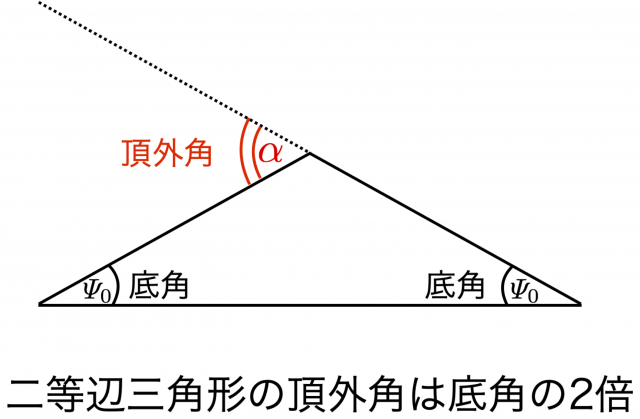
最後に,上図から曲がり角 \(\alpha\) は,「二等辺三角形の頂外角は底角の2倍」という(ユークリッド幾何学で「のみ」成り立つ)関係を使えば,
$$ \alpha = 2 \varPsi_0 = \frac{2 r_g}{b}$$
となる。\(\varPsi_0\) 自体の計算の際には,\( r \rightarrow \infty\) での漸近的平坦性を仮定してないことに注意。だが,曲がり角 \(\alpha\) の定義の際には,漸近的平坦性どころか,光が伝播する空間全体でユークリッド幾何学の仮定を用いていることにも留意されたい。
「まっすぐな」線は曲がるのか?
「まっすぐな」線は曲がるのか?というなんだか禅問答(適切な例えかわからないが)みたいな問題に対しては,読者自身が納得できるような解答を自分で探すのが一番だと思うが,以下のような例え話はどうでしょうかねぇ。
現実世界では光は曲がった空間(下図では Schwarzschild と書いたほう)をひたすら測地線方程式にしたがって「まっすぐ」伝播していく。これを(Flat と書いたほうの)ユークリッド空間に射影してみると,その経路はまっすぐには見えない。
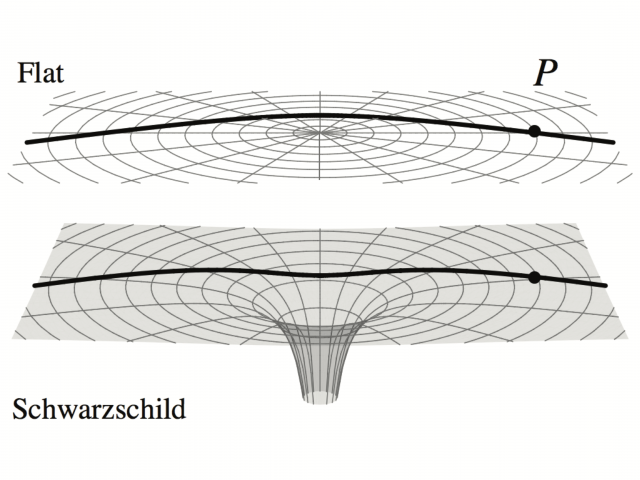
ユークリッド幾何学が成り立つような平坦な空間に射影した経路は,以下のように「曲がり角」 \(\alpha\) だけ曲がっていると解釈される… とこんな考え方もあるということで。
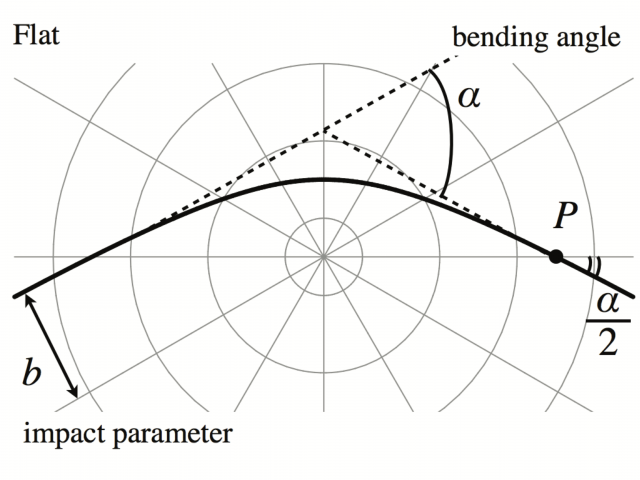
参考: