なぜ電磁場の変換性を考える必要があるのだろうか?以下の例でわかるように,観測可能な物理的現象が観測者の運動状態(速度)によらずに矛盾なく決められるために,必要なのである。
電線と運動する荷電粒子
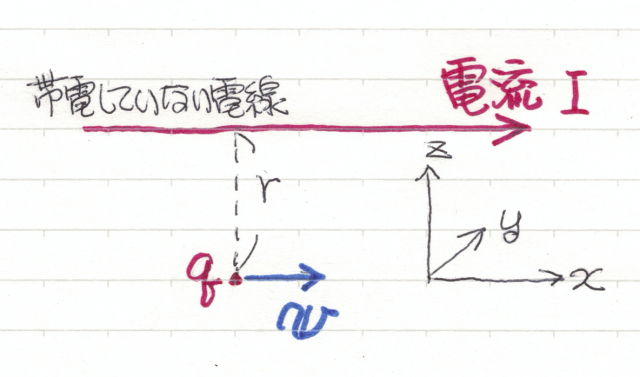
図のように,全体として帯電していない(つまり \(\rho=0\) だから電場をつくらない)電線に電流 \(I\) が流れている。図のように座標軸を設定すると \(\vec{I} = (I, 0, 0)\)。
このとき,電線から距離 \(r\) 離れたところを電線に平行な速度 \(\vec{v} = (v, 0, 0)\) で運動する電荷 \(q>0\) をもつ荷電粒子が受けるローレンツ力は?
解答例:
まず電線は帯電していないので,電場はゼロ。\(\vec{E} = \vec{0}\)。
しがたって,電荷がうけるローレンツ力は
$$\vec{F} = q \vec{v} \times \vec{B}$$
直線電流によってつくられる磁場はアンペールの法則から,荷電粒子の位置では
$$\vec{B} = (0, B_y, 0), \quad B_y = \frac{I}{2\pi\varepsilon_0 c^2 r}$$
したがって,荷電粒子にはたらくローレンツ力の各成分は
\begin{eqnarray}
F_x &=& q (v_y B_z -v_z B_y) = 0\\
F_y &=& q(v_z B_x -v_x B_z) = 0\\
F_z &=& q(v_x B_y -v_y B_x) = \frac{q v I}{2\pi\varepsilon_0 c^2 r}
\end{eqnarray}
よって,荷電粒子は電線に引き付けられる向きに力がはたらく。
これを速度 \(\vec{v}\) で運動する慣性系でみると…
上記の問題を,荷電粒子の速度 \(\vec{v}\) で運動する慣性系からみると,速度の合成則により,この慣性系の観測者からみる荷電粒子の速度 \(\vec{v}’\) は
$$ \vec{v}’ = \vec{v}-\vec{v} = \vec{0}$$
となり,ローレンツ力はゼロになってしまう!?
$$\vec{F}’ = q \vec{v}’ \times \vec{B} = \vec{0}$$
力がはたらかなければ電線に引き付けられることはない。荷電粒子の運動は,観測する座標系によって変わってしまうのであろうか?
果たして… ?
電磁場の相対性
観測する座標系の違いによって物理学的な運動が異なってしまうことは,ありえない。上の議論はどこかがおかしい。
すでに「電磁場の変換」で説明したように,荷電粒子の速度 \(\boldsymbol{v}\) で運動する観測者は,
\begin{eqnarray}
\bar{E}_{\perp} &=& \frac{E_{\perp}+ (\boldsymbol{v}\times\boldsymbol{B})_{\perp}}{\sqrt{1 -v^2}}\\
\end{eqnarray}
という電場を感じるので,この電場によって,この問題のようにたとえ \(E_{\perp} = 0\) であっても!やはり荷電粒子は電線に引きつけられる力を受けて運動する。
4元力としての相対論的なローレンツ力
荷電粒子の4元速度を \(\boldsymbol{v} = v^{\mu} \boldsymbol{e}_{\mu}\) とすると,この荷電粒子が受ける4元力としての相対論的なローレンツ力の成分 \(f_{\mu}\) は以下のように定義される。
$$f_{\mu} \equiv q F_{\mu\nu} v^{\nu}$$ここで \(F_{\mu\nu}\) は電磁場テンソルである。
観測者 \(A\) からみると,荷電粒子は速度 \(v \boldsymbol{e}\) で運動しているので,4元速度の合成則から
$${v}^{\mu} = \frac{{u}^{\mu} + v {e}^{\mu}}{\sqrt{1 -v^2}}$$
したがって相対論的なローレンツ力は
\begin{eqnarray}
f_{\mu} &=& q F_{\mu\nu} v^{\nu} \\
&=& q F_{\mu\nu} \frac{{u}^{\mu} + v {e}^{\mu}}{\sqrt{1 -v^2}}\\
&=& q \frac{F_{\mu\nu}{u}^{\mu} + F_{\mu\nu} v {e}^{\mu}}{\sqrt{1 -v^2}} \\
&=& q \frac{E_{\mu} + (\boldsymbol{v}\times\boldsymbol{B})_{\mu}}{\sqrt{1 -v^2}}
\end{eqnarray}
上記の結果からもわかるように,4元力としての相対論的なローレンツ力の空間成分は,いわゆる(3次元的な)ローレンツ力 \(q (\vec{E} + \vec{v}\times\vec{B})\) とはローレンツ因子 \(\gamma \equiv 1/\sqrt{1-v^2}\) の分だけ異なっている。
一方,荷電粒子と同じ速度で運動している観測者 \(B\) からみると,
$${v}^{\mu} = \bar{u}^{\mu} $$
したがって相対論的なローレンツ力は
\begin{eqnarray}
f_{\mu} &=& q F_{\mu\nu} v^{\nu} \\
&=& q F_{\mu\nu} \bar{u}^{\nu} \\
&=& q \bar{E}_{\mu}
\end{eqnarray}