Return to SymPy 演習

1. SymPy の基本事項と主な定数・関数

SymPy で数学的計算を行うための基本と，SymPy で定義されている主な定数や関数について。

SymPy の import

In [1]:
from sympy.abc import *
from sympy import *

init_printing()

表記などの約束事

Python の実行に際して，いくつか表記についての約束事があります。代表的なものを以下に示します。

コメント #

コメント (実行に影響しない注釈) を入れたいときは，# を書きます。

In [2]:
1 + 2 + 3
Out[2]:
$\displaystyle 6$
In [3]:
1 + 2 # + 3
Out[3]:
$\displaystyle 3$

四則演算とかっこ ()

加法 +，減法 -，乗法 *，除法 / における優先順位は数学と同じです。優先して計算したい箇所は ( ) で 囲みます。[ ] や { } は優先順位の指定には使いません。

In [4]:
1 + 2 * 3
Out[4]:
$\displaystyle 7$
In [5]:
(1 + 2) * 3
Out[5]:
$\displaystyle 9$

累乗（べき乗）**

** は累乗（べき乗）を表します。 2 の 100 乗 ($2^{100}$) のような大きい数でも，厳密な結果を出力します。

In [6]:
2**100
Out[6]:
$\displaystyle 1267650600228229401496703205376$

浮動小数点表示 N()

SymPy の N() 関数を使って浮動小数点表示で近似値を出力させることもできます。

In [7]:
N(2**100)
Out[7]:
$\displaystyle 1.26765060022823 \cdot 10^{30}$

N() で桁数を指定する例：以下では有効桁数5桁で表示させています。

In [8]:
N(2**100, 5)
Out[8]:
$\displaystyle 1.2677 \cdot 10^{30}$

○練習：3, 2, 1 でつくる最大数

数字の 3 と 2 と 1 を 1 個ずつ使った演算でつくることができる最大の整数は?

ヒント:

(1 + 2) × 3 = 9 じゃ全然だめ。そのまま並べると 321 ですが，累乗を使うともっと大きい数をつくることができます。
$21^3$ とか，$31^2$ とか，$2^{31}$ とか…

In [ ]:
In [ ]:
In [ ]:

割り算 /，商 //，剰余 %

Python では除算 / は常に浮動小数点数型の実数を返します。

In [9]:
3/21
Out[9]:
$\displaystyle 0.142857142857143$

// 演算子は整数除算を行い、小数部を切り捨てた整数値（商）を返します。剰余は、% で求めます。

In [10]:
17 // 3
Out[10]:
$\displaystyle 5$
In [11]:
17 % 3
Out[11]:
$\displaystyle 2$
In [12]:
17 == 3 * (17//3) + (17%3)
Out[12]:
True

有理数 Rational()

有理数として分数をあつかう際は，SymPy の Rational() を使います。

以下では $\displaystyle \frac{3}{21} \Rightarrow \frac{1}{7}$ に自動的に約分して表示します。

In [13]:
# 3/21 = 1/7

Rational(3, 21)
Out[13]:
$\displaystyle \frac{1}{7}$

代入 =

変数に式や値を代入するときは，等号記号 = を使います。

変数 a に $100+3/21$
を代入し，a の値を表示させる例です。

In [14]:
a = 100 + Rational(3,21)
a
Out[14]:
$\displaystyle \frac{701}{7}$

変数 a に代入された値を使って，さらに計算を続けてみます。

In [15]:
(a - 100) * 7
Out[15]:
$\displaystyle 1$

$\displaystyle a = a -\frac{1}{7}$ は等式・方程式としては成り立ちませんが，Python（やその他のプログラミング言語）では，変数 $a$ に直前までに代入されている値から $\displaystyle \frac{1}{7}$ を引いた右辺の答えを あたらめて 左辺の変数 $a$ に代入する，ということになりますよねぇ。

In [16]:
a = 100 + Rational(3,21)
a = a - Rational(1, 7)
a
Out[16]:
$\displaystyle 100$

a = a - Rational(1, 7) と同じことを Python ではインクリメント += やデクリメント -= を使って書くこともできます。例えば…

In [17]:
a = 100 + Rational(3,21)
display(a)
a -= Rational(1, 7)
display(a)
a += Rational(1, 7)
display(a)
$\displaystyle \frac{701}{7}$
$\displaystyle 100$
$\displaystyle \frac{701}{7}$

一時的代入 .subs()

$b = 3 a$ と定義し，…

In [18]:
# 上で a に値が代入されているので初期化
var('a')

b = 3*a
b
Out[18]:
$\displaystyle 3 a$

b.subs(a, 2) で一時的に $a$ に値 $2$ を代入すると…

In [19]:
# 上で a に値が代入されているので初期化
var('a')

b = 3*a
b.subs(a, 2)
Out[19]:
$\displaystyle 6$

b.subs(a, 2) $\displaystyle = 3 a \bigr|_{a=2} = 3\times 2 = 6$ を出力しますが，

$b$ の定義そのものは変わりません。

In [20]:
b
Out[20]:
$\displaystyle 3 a$

等式 Eq()

等式は Eq(左辺, 右辺) のように定義します。= は Python では代入を表すために使われてるので，左辺 = 右辺 のように書くと右辺の量を左辺の変数に代入する，という意味になり，左辺と右辺は等しい，という等式の意味にはなりません。

Eq(左辺, 右辺) については「方程式」の項であらためて説明するほか，以下では左辺を SymPy で計算すると右辺のような量になる，という表示をさせるために使います。

実行結果の非表示 (;)

以下の例では，多項式 $x^2 + 3 x + 2$ を変数 eq に代入しています。

In [21]:
eq = x**2 + 3*x + 2

代入や関数の定義のときは，式や変数の値が表示されません。

eq の内容を知りたいときは，Shift + Enter すれば実行結果が表示されますが，文末に ; をつけると結果が出力されません。

In [22]:
eq
Out[22]:
$\displaystyle x^{2} + 3 x + 2$
In [23]:
eq;

因数分解 factor()

eq に代入された多項式を factor() で因数分解します。

In [24]:
factor(eq)
Out[24]:
$\displaystyle \left(x + 1\right) \left(x + 2\right)$

展開 expand()

$(x-2)^4$ を expand() で展開します。

In [25]:
expand((x-2)**4)
Out[25]:
$\displaystyle x^{4} -8 x^{3} + 24 x^{2} -32 x + 16$

直前の出力結果の参照 _

直前の出力結果は _ で参照できます。

直前の結果を factor() で因数分解します。

In [26]:
factor(_)
Out[26]:
$\displaystyle \left(x -2\right)^{4}$

主な定数

SymPy で定義されている主な定数についてまとめます。

円周率 $\pi =$ pi

SymPy では円周率 $\pi$ は pi です。

In [27]:
pi
Out[27]:
$\displaystyle \pi$

浮動小数点で近似値を表示するには N() を使います。

In [28]:
N(pi)
Out[28]:
$\displaystyle 3.14159265358979$

参考までに，N() を使って円周率 $\pi$ を 30桁まで表示させる例です。

In [29]:
N(pi, 30)
Out[29]:
$\displaystyle 3.14159265358979323846264338328$

ネイピア数（自然対数の底）$e =$ E

SymPy では自然対数の底 $e$ は E です。

In [30]:
E
Out[30]:
$\displaystyle e$

N() で小数点表示させると…

In [31]:
N(E)
Out[31]:
$\displaystyle 2.71828182845905$

ネイピア数 $e$ は元々以下のような定義で導入されました。

\begin{eqnarray}
\lim_{h \rightarrow 0} \frac{e^{h} -1}{h} &=& 1\\
\therefore\ e &=& \lim_{h \rightarrow 0} \left(1 + h\right)^{\frac{1}{h}}
\end{eqnarray}

この極限を SymPy で確認してみます。

極限 limit()

SymPy では極限は limit() または Limit().doit() です。Limit() は極限の式を表示するだけで実行はしません。

$\displaystyle \lim_{h \rightarrow 0} \frac{e^{h} -1}{h} = $ limit((E**h-1)/h, h, 0)

Eq(左辺, 右辺) は等式をあらわし，左辺の式を SymPy で計算すると右辺の式になる，と表示させるために使ってみます。

In [32]:
Eq(Limit((E**h-1)/h, h, 0),
   limit((E**h-1)/h, h, 0))
Out[32]:
$\displaystyle \lim_{h \to 0^+}\left(\frac{e^{h} -1}{h}\right) = 1$

$\displaystyle \lim_{h\rightarrow 0} \left(1+h\right)^{\frac{1}{h}} = $ limit((1+h)**(1/h), h, 0) $= \cdots$

In [33]:
Eq(Limit((1+h)**(1/h), h, 0), 
   limit((1+h)**(1/h), h, 0))
Out[33]:
$\displaystyle \lim_{h \to 0^+} \left(h + 1\right)^{\frac{1}{h}} = e$

虚数単位 $i =$ I

SymPy では虚数単位 $i$ は I

$\displaystyle i^2 = -1$ を確認します。

In [34]:
I**2
Out[34]:
$\displaystyle -1$
オイラーの等式

無理数 $e$，$\pi$，虚数単位 $i$，整数 $1$ および $0$ の間のすてきな関係，オイラーの等式 $$e^{i\pi} +1 = 0$$

In [35]:
E**(I * pi) + 1 == 0
Out[35]:
True

無限大 $\infty =$ oo

無限大は定数ではないが，SymPy では $\infty = $ oo と小文字の o（オー）を2つ並べて書きます。（ちょっとかわいい。）

$\displaystyle \lim_{x \rightarrow \infty} e^{-x}$ = limit(exp(-x), x, oo) $= \cdots$

In [36]:
limit(exp(-x), x, oo)
Out[36]:
$\displaystyle 0$

主な関数

SymPy で定義されている主な関数（初等関数など）についてまとめます。

べき関数 x**n

$\displaystyle x^n = $ x**n

平方根 sqrt()

$\displaystyle \sqrt{x} = x^{\frac{1}{2}} =$ sqrt(x)

In [37]:
print('sqrt(64) =', sqrt(64))
print('64**(1/2) =', 64**(Rational(1,2)))

sqrt(64) = 8
64**(1/2) = 8
平方根について補足

うっかり $\sqrt{x^2} = x$ としないように。SymPy はデフォルトでは…

In [38]:
sqrt(x**2)
Out[38]:
$\displaystyle \sqrt{x^{2}}$

$x$ を実数としてやると…

In [39]:
var('x', real=True)

sqrt(x**2)
Out[39]:
$\displaystyle \left|{x}\right|$

$x$ を正の実数とすると…

In [40]:
var('x', positive=True)

sqrt(x**2)
Out[40]:
$\displaystyle x$
In [41]:
# 実数の設定を初期化する
var('x')

sqrt(x**2)
Out[41]:
$\displaystyle \sqrt{x^{2}}$
絶対値 abs()

abs(x) は $x$ の絶対値 $|x|$ です。

複素数 $x = a + b i$ については，$|x| = \sqrt{a^2 + b^2}$ であるため，
$\sqrt{x^2} \neq |x|$ です。例として $x = 1 + 3 i$ とすると

$\sqrt{x} =$ sqrt((1 + 3*I)**2) $= \cdots$

In [42]:
sqrt((1 + 3*I)**2)
Out[42]:
$\displaystyle 1 + 3 i$

一方，

$|x| =$ abs(1 + 3*I) $= \cdots$

In [43]:
abs(1 + 3*I)
Out[43]:
$\displaystyle \sqrt{10}$

$\sqrt{x^2} \neq |x|$ であることは明らかです。

指数関数 exp()

$a$ を底とする指数関数 $a^x$ のうち，とくにネイピア数 $e$ を底とする指数関数は

$e^x =$ exp(x) $=$ E**x

指数法則

$1. \ a^x\,a^y = a^{x+y}$

$\displaystyle 2. \ \left(a^x\right)^y = a^{xy}$

$3. \ (a b)^x = a^x\, b^x$

念のため，SymPy で確認してみる。

変数 $a, b, x, y$ を念のため初期化。

In [44]:
var('a b x y')
Out[44]:
$\displaystyle \left( a, \ b, \ x, \ y\right)$

$1. \ a^x\,a^y = a^{x+y}$ は simplify() で示せる。

In [45]:
f = a**x * a**y
Eq(f, simplify(f))
Out[45]:
$\displaystyle a^{x} a^{y} = a^{x + y}$

$3. \ (a b)^x = a^x\, b^x$ は expand() に force=True オプションをつければ示せる。

In [46]:
g = (a*b)**x
Eq(g, expand(g, force=True))
Out[46]:
$\displaystyle \left(a b\right)^{x} = a^{x} b^{x}$

$\displaystyle 2. \ \left(a^x\right)^y = a^{xy}$ が成り立つことを SymPy で確認するにはどうしたらいいんでしょうかねぇ。

In [ ]:

対数関数 log()

一般に $b$ を底とする対数関数は $\log_b x =$ log(x, b)

自然対数 $\displaystyle \log_e x = \log x =$ log(x)

自然対数 $\log x$ は指数関数 $e^x$ の逆関数であるから，

$\displaystyle e^{\log x} = x$ や $\displaystyle \log \left(e^x\right) = x$ が成り立ちます。確認してみます。

In [47]:
exp(log(x))
Out[47]:
$\displaystyle x$

$\displaystyle \log \left(e^x\right) = x$ を示すには，以下のように expand_log() に force=True オプションをつけて。

In [48]:
Eq(log(exp(x)), 
   expand_log(log(exp(x)), force=True))
Out[48]:
$\displaystyle \log{\left(e^{x} \right)} = x$
常用対数 log( , 10)

$10$ を底とする常用対数 $\log_{10}$ は以下のように…

$\displaystyle \log_{10} 1000 = \log_{10} 10^3 = 3$

In [49]:
log(1000, 10)
Out[49]:
$\displaystyle 3$
参考：log10 の import

以下のように log10() を import して使うこともできるようです。

In [50]:
from sympy.codegen.cfunctions import log10

log10(1000)
Out[50]:
$\displaystyle 3$
対数法則

$1.\ \log(x y) = \log x + \log y$

$2. \ \log(x^y) = y \log x$

これらを確認するにも， expand_log() に force=True オプションが必要です。

In [51]:
Eq(log(x*y), 
   expand_log(log(x*y), force=True))
Out[51]:
$\displaystyle \log{\left(x y \right)} = \log{\left(x \right)} + \log{\left(y \right)}$
In [52]:
Eq(log(x**y), 
   expand_log(log(x**y), force=True))
Out[52]:
$\displaystyle \log{\left(x^{y} \right)} = y \log{\left(x \right)}$

三角関数 sin(x), cos(x), tan(x)

$\sin x =$ sin(x), $\cos x =$ cos(x), $\tan x =$ tan(x)

$\sin^2 x + \cos^2 x = 1$ を確認します。

簡単化 simplify()

simplify() を使って簡単化させます。

In [53]:
simplify(sin(x)**2 + cos(x)**2)
Out[53]:
$\displaystyle 1$

$\displaystyle 1 + \tan^2 x = \frac{1}{\cos^2 x}$ が成り立つことも確認しておきましょう。

In [ ]:
引数の単位

三角関数の引数の単位はラジアンです。

$\displaystyle \sin \frac{\pi}{3}$ の値は…

In [54]:
sin(pi/3)
Out[54]:
$\displaystyle \frac{\sqrt{3}}{2}$
度からラジアンへの変換 rad()

度（°）からラジアンへの変換は SymPy では rad() を使います。

$\displaystyle 30^{\circ} = \frac{\pi}{6}\, \mbox{(rad)}$ を確かめるには…

In [55]:
rad(30)
Out[55]:
$\displaystyle \frac{\pi}{6}$
ラジアンから度への変換 deg()

逆に，ラジアンから度（°）への変換は SymPy では deg() を使います。

$\displaystyle \frac{\pi}{4}\, \mbox{(rad)} = 45^{\circ}$ を確かめるには…

In [56]:
deg(pi/4)
Out[56]:
$\displaystyle 45$
加法定理

$\sin (x + y) = \sin x \, \cos y + \cos x \, \sin y$ および

$\cos (x + y) = \cos x \, \cos y –\sin x \, \sin y$ の確認。

三角関数を「展開」するときは，expand() 関数に trig = True オプションをつけます。

In [57]:
Eq(sin(x + y), 
   expand(sin(x + y), trig = True))
Out[57]:
$\displaystyle \sin{\left(x + y \right)} = \sin{\left(x \right)} \cos{\left(y \right)} + \sin{\left(y \right)} \cos{\left(x \right)}$
In [58]:
Eq(cos(x + y), 
   expand(cos(x + y), trig = True))
Out[58]:
$\displaystyle \cos{\left(x + y \right)} = -\sin{\left(x \right)} \sin{\left(y \right)} + \cos{\left(x \right)} \cos{\left(y \right)}$
○練習：$\tan$ の加法定理

$\tan(x+y)$ を $\tan x$ と $\tan y$ を使って表しなさい。

In [ ]:
In [ ]:
○練習：三倍角の公式

$\sin 3x$ を $\sin x$ だけを使って表しなさい。

In [ ]:
逆三角関数 asin(x), acos(x), atan(x)
逆三角関数は三角関数の逆関数として定義され，それぞれ
$\sin^{-1} x = \arcsin x = $ asin(x)
 $\cos^{-1} x = \arccos x = $ acos(x)
 $\tan^{-1} x = \arctan x = $ atan(x)
と書きます。逆関数ですから以下の関係が成り立つはずです。
$\sin\left(\sin^{-1} x\right) = x$
 $\cos\left(\cos^{-1} x\right) = x$
 $\tan\left(\tan^{-1} x\right) = x$
確認してみます。
In [59]:
sin(asin(x))

Out[59]:
$\displaystyle x$
In [60]:
cos(acos(x))

Out[60]:
$\displaystyle x$
In [61]:
tan(atan(x))

Out[61]:
$\displaystyle x$
しかし，$\sin^{-1} \left(\sin x\right) = x$ などとは一般にはなりません。
In [ ]:
 

○練習：逆三角関数の引数に三角関数を入れると
逆三角関数は三角関数の逆関数ではあるが，一般には以下の式は成り立たない。
\begin{eqnarray}
 \sin^{-1} \left(\sin x\right) &=& x \\
 \cos^{-1} \left(\cos x\right) &=& x \\
 \tan^{-1} \left(\tan x\right) &=& x
 \end{eqnarray}
このことを反例を挙げて（つまり $x$ にある値を入れると上記の等号が成り立たないことを）示せ。
また，なぜ成り立たないのか理由を考えてみよ。
In [ ]:
○練習：逆三角関数の間の関係式
以下の関係を確かめよ。
$\displaystyle \cos^{-1} x + \sin^{-1} x = \frac{\pi}{2}
 $
In [62]:
# ヒント acos(x) を asin(x) を使って書き直す

In [ ]:
 

以下の関係式を SymPy で確かめるのは難しそうです…
$\displaystyle \tan^{-1} x + \tan^{-1} \frac{1}{x} =  \frac{\pi}{2}
 $
In [ ]:
 

In [ ]:
 

○練習：屋根勾配
問：人生になぜ「逆三角関数」が必要か。
 答：家を建てるために必要です。ログハウスを建てた本人が言っているのだら間違いない！
大工さんは，家の屋根の勾配は角度ではなく，伝統的に 3 寸勾配，4 寸勾配のように水平方向に 1 尺(10 寸)に対して垂直方向に何寸立ち上がるかで示します。
一方で，傾斜天井につける照明器具を電気屋さんに問い合わせると，傾斜角度は何度だと聞かれます。
つまり，ログハウスを建てるためには逆三角関数，特に $\tan^{-1} x$ が必要になるわけです！？
図のログハウスの屋根は 8 寸勾配です。
 傾斜角度にすると何度ですか? 小数点以下1桁までの数値で。
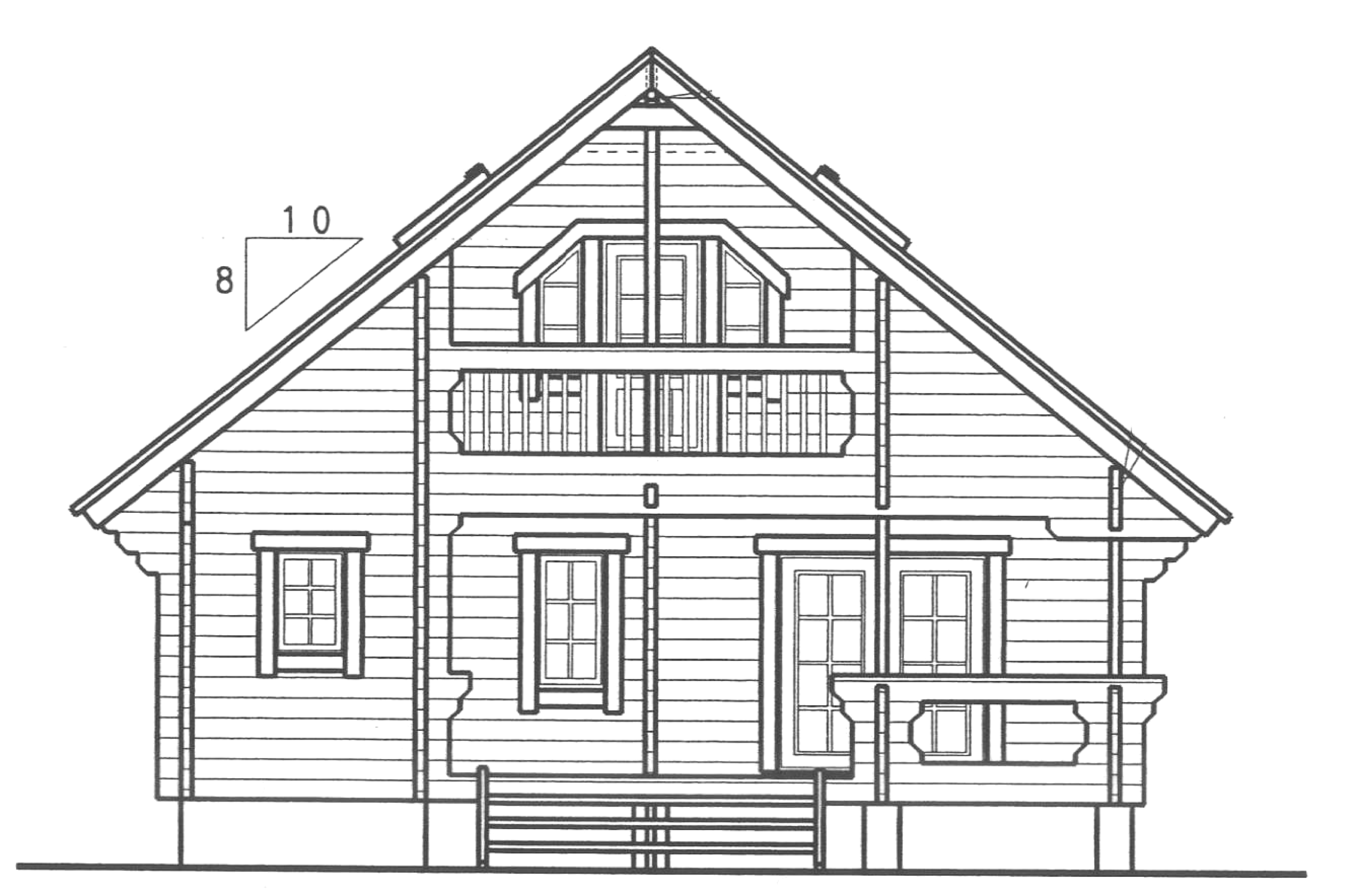
8 寸勾配の傾斜角度とは，傾きが $\displaystyle \tan \theta = \frac{8}{10}$ となる角度 $\theta$ を度で表したものだから…
In [ ]:
 

以下のように 1 寸勾配から 10 寸勾配（矩勾配　かねこうばい）まで表示させてください。
 1 寸勾配の傾斜角度は ##.#°
 2 寸勾配の傾斜角度は ##.#°
 3 寸勾配の傾斜角度は ##.#°
     ...

10 寸勾配の傾斜角度は ##.#°
双曲線関数 sinh(x), cosh(x), tanh(x)
双曲線関数は指数関数を使って以下のように定義されます。
$\displaystyle \cosh x \equiv \frac{e^{x} + e^{-x}}{2} =$ cosh(x)
$\displaystyle \sinh x \equiv \frac{e^{x} -e^{-x}}{2} =$ sinh(x)
$\displaystyle \tanh x \equiv \frac{\sinh x}{\cosh x} = \frac{e^{x} -e^{-x}}{e^{x} + e^{-x}} =$ tanh(x)
○練習：双曲線関数を指数関数で表す
双曲線関数を指数関数 exp() で書き直すには，書き直す関数に .rewrite(exp) を付けます。
In [63]:
Eq(cosh(x),
   cosh(x).rewrite(exp))

Out[63]:
$\displaystyle \cosh{\left(x \right)} = \frac{e^{x}}{2} + \frac{e^{-x}}{2}$
$\sinh x, \ \tanh x$ についても同様に指数関数で書き直してください。
In [ ]:
In [ ]:
$\cosh^2 x -\sinh^2 x = 1$ を SimPy で確認してみます。simplify() で「簡単化」します。
In [64]:
eq = cosh(x)**2 - sinh(x)**2

Eq(eq, simplify(eq))

Out[64]:
$\displaystyle -\sinh^{2}{\left(x \right)} + \cosh^{2}{\left(x \right)} = 1$
$1 -\tanh^2 x$ も簡単化してみてください。
In [ ]:
 

加法定理
双曲線関数にも，三角関数の場合と似たような加法定理があります。expand() は「展開」する関数です。双曲線関数を「展開」するときは，（双曲線関数は三角ではありませんが）三角関数の場合と同様に
trig = True

オプションをつけます。
$\displaystyle \cosh (x + y) = \cosh x\, \cosh y + \sinh x\, \sinh y$ を確認します。
In [65]:
Eq(expand(cosh(x + y)), 
   expand(cosh(x + y), trig = True))

Out[65]:
$\displaystyle \cosh{\left(x + y \right)} = \sinh{\left(x \right)} \sinh{\left(y \right)} + \cosh{\left(x \right)} \cosh{\left(y \right)}$
逆に，右辺の式が左辺になることを示すには，simplify() で良さそうです。
In [66]:
sscc = sinh(x)*sinh(y) + cosh(x)*cosh(y)

Eq(sscc, simplify(sscc))

Out[66]:
$\displaystyle \sinh{\left(x \right)} \sinh{\left(y \right)} + \cosh{\left(x \right)} \cosh{\left(y \right)} = \cosh{\left(x + y \right)}$
○練習：双曲線関数の加法定理
$\sinh(x+y)$，$\tanh(x+y)$ についての加法定理を確認しなさい。
In [ ]:
 

In [ ]:
 

逆双曲線関数 asinh(x), acosh(x), atanh(x)
逆双曲線関数は双曲線関数の逆関数として定義され，それぞれ
$\sinh^{-1} x = \mbox{arsinh}\ x = $ asinh(x)
 $\cosh^{-1} x = \mbox{arcosh}\ x = $ acosh(x)
 $\tanh^{-1} x = \mbox{artanh}\ x = $ atanh(x)
と書きます。（ar であり，arc とは書かない。）
逆関数ですから以下の関係が成り立つはずです。
$\sinh\left(\sinh^{-1} x\right) = x$
 $\cosh\left(\cosh^{-1} x\right) = x$
 $\tanh\left(\tanh^{-1} x\right) = x$
確認してみます。
In [67]:
sinh(asinh(x))

Out[67]:
$\displaystyle x$
In [68]:
cosh(acosh(x))

Out[68]:
$\displaystyle x$
In [69]:
tanh(atanh(x))

Out[69]:
$\displaystyle x$
双曲線関数は指数関数を使って表すことができましたが，逆双曲線関数は対数関数 log() を使って表すことができます。
以下のように，書き直したい双曲線関数に .rewrite(log) を付けます。
In [70]:
Eq(asinh(x), 
   asinh(x).rewrite(log))

Out[70]:
$\displaystyle \operatorname{asinh}{\left(x \right)} = \log{\left(x + \sqrt{x^{2} + 1} \right)}$
$\cosh^{-1} x, \ \tanh^{-1}x$ についても以下のようになることを確認しなさい。
\begin{eqnarray}
 \cosh^{-1} x &=&  \log\left(x + \sqrt{x^2-1}\right) \\
 \tanh^{-1} x &=& \frac{1}{2} \log\left(\frac{1+x}{1-x} \right)
 \end{eqnarray}
In [ ]:
 

In [ ]:
 

人類の至宝：オイラーの公式
$$e^{i x} = \cos x + i \sin x$$
オイラーの公式を確認するために，指数関数 $e^{i x}$ を .rewrite(cos) または .rewrite(sin) をつけて三角関数で書き直してみます。SymPy では虚数単位 $i$ は I です。
In [71]:
Eq(exp(I*x), 
   exp(I*x).rewrite(cos))

Out[71]:
$\displaystyle e^{i x} = i \sin{\left(x \right)} + \cos{\left(x \right)}$
逆に，三角関数を指数関数を使って表してみます。
In [72]:
cos(x).rewrite(exp)

Out[72]:
$\displaystyle \frac{e^{i x}}{2} + \frac{e^{- i x}}{2}$
In [73]:
sin(x).rewrite(exp)

Out[73]:
$\displaystyle -\frac{i \left(e^{i x} -e^{- i x}\right)}{2}$
以上のことから
\begin{eqnarray}
 \cos x &=& \frac{e^{ix} + e^{-ix}}{2} \\
 \sin x &=& \frac{e^{ix} -e^{-ix}}{2 i}
 \end{eqnarray}
であることが確認できした。
三角関数と双曲線関数の関係
三角関数と双曲線関数は，ただまぎらわしいほどに似た表記なだけでなく，アイで結ばれた密接な関係であることを SymPy で確認します。
In [74]:
cos(I*x)

Out[74]:
$\displaystyle \cosh{\left(x \right)}$
In [75]:
sin(I*x)

Out[75]:
$\displaystyle i \sinh{\left(x \right)}$
… ということで以下のことが確認できました。
\begin{eqnarray}
 \cos (i x) &=& \cosh x \\
 \sin (i x) &=& i \sinh x
 \end{eqnarray}
○練習：双曲線関数と三角関数の関係
$\cosh (i x)$ や $\sinh (i x)$ を三角関数を使ってあらわせ。
In [ ]:
 

In [ ]:
 

階乗 factorial()
$4$ の階乗 $4!$ の計算をします。SymPy では，階乗は factorial() 関数を使います。
factorial(4) $= 4! =4×3×2×1=24$
In [76]:
factorial(4)

Out[76]:
$\displaystyle 24$
factorial2()
factorial2() 関数は，一つおきの階乗の計算をします。
factorial2(5) $= 5!!=5×3×1=15$ です。
In [77]:
factorial2(5)

Out[77]:
$\displaystyle 15$
総和 summation()
（sum() は Python の組み込み関数として定義済みなので）SymPy で総和を求める関数は summation() であり，
$\displaystyle \sum_{i = 1}^n a_i =$ summation(a(i), (i, 1, n)) $=$ Sum(a(i), (i, 1, n)).doit()
参考：Sum() と summation()
Sum() は総和の表示をするだけで実際に総和は行いません。総和を実行するには，Sum().doit() のように .doit() を追加します。
summation() を使えば即総和を実行します。
例：
$\displaystyle \sum_{i = 1}^n i =$ summation(i, (i, 1, n))
$\displaystyle \sum_{i = 1}^n i^2 =$ summation(i**2, (i, 1, n))
SymPy の summation() は一般の $n$ の値について数列の総和の公式を返してくれます。
In [78]:
Eq(Sum(i, (i, 1, n)),
   summation(i, (i, 1, n)).factor())

Out[78]:
$\displaystyle \sum_{i=1}^{n} i = \frac{n \left(n + 1\right)}{2}$
In [79]:
Eq(Sum(i**2, (i, 1, n)),
   summation(i**2, (i, 1, n)).factor())

Out[79]:
$\displaystyle \sum_{i=1}^{n} i^{2} = \frac{n \left(n + 1\right) \left(2 n + 1\right)}{6}$
もちろん，特定の $n$ の値，例えば $n=10$ の場合の総和も計算します。
In [80]:
Eq(Sum(i, (i, 1, 10)),
   summation(i, (i, 1, 10)))

Out[80]:
$\displaystyle \sum_{i=1}^{10} i = 55$
In [81]:
Eq(Sum(i**2, (i, 1, 10)),
   summation(i**2, (i, 1, 10)))

Out[81]:
$\displaystyle \sum_{i=1}^{10} i^{2} = 385$
関数の定義 def f(x):
Python や SymPy で定義されている組み込み関数以外にも，Python の記法で関数を定義することができます。
たとえば $ f(x) := x^2$ のような関数 $f(x)$ を定義するには，Python の記法で…
In [82]:
def f(x):
    return x**2

def f(x): で関数を定義しただけでは，実行結果が表示されません。f(x) の定義を確認するには，あたらめて以下のように表示させます。
In [83]:
f(x)

Out[83]:
$\displaystyle x^{2}$
$f(4) = 4^2 = 16$
In [84]:
f(4)

Out[84]:
$\displaystyle 16$
○練習：等差数列の和
  1. 初項が $a$，公差が $d$ である等差数列の一般項を関数 b(n) として定義せよ。
  2. 上記の等差数列の初項（第1項）から第 $n$ 項までの和は？
In [ ]:
In [ ]:
 

○練習：等比数列の和
  1. 初項が $a$，公比が $r$ である等比数列のを関数 c(n) として定義せよ。
  2. 上記の等比数列の初項（第1項）から第 $n$ 項までの和は？
In [ ]:
In [ ]: