2つの量（あるいは数）の関係を2次元平面にプロットしてそれを何らかの関数でフィッティングする、ということはある種の学問や現場ではよく行われます。そして与えられた関数の形に対して最もよくフィットするパラメータを求める方法として、最小二乗法（Least Squares Method）が非常によく使われます（他の方法を使おうものなら「それには何か意図があるのですか？」と問い詰められるレベルで標準的な方法だと思います）。最小二乗法とは、文字通りに残差の二乗の和（残差平方和）が最小になるようなパラメータを求める、というものです。
与えられたデータを簡単な形の関数でフィッティングする機能は、汎用の表計算ソフトにも当然に備わっています。深く考えずに「このソフトの出力結果は最小二乗法で求めたものでしょ」と思い込んでしまいがちですが、例えば指数関数でフィッティングすると、ソフトの出力結果は一般に残差平方和を最小にするものにはなりません。
実例
とりあえずフィッティングする
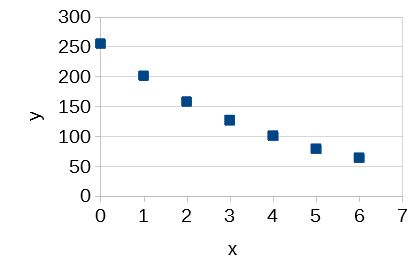
まずは例を見てみましょう。2つの量xとyを測定して、図1のようなデータが得られたとします（数値は図3を参照のこと）。単位系は今回の話の本質とは関係ないので、出てくる量はすべて無次元であると考えてください。
おっと、ここではいつものようにLibreOffice Calcを使って話を進めていきます。MS Excelを使っても、同じような現象を確認できると思います。
図1の散布図を見ると、いかにも指数関数 
でフィッティングできそうなプロットの並びになっています。ということで、フィッティングしてみました。その結果が図2です。（念のため…LibreOffice Calcではプロット上で右クリックし、コンテキストメニューから[近似曲線の追加]を選びます。MS Excelでもほぼ同様の操作です。）
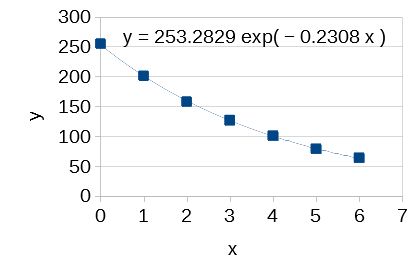
一瞥する限りでは悪くないフィッティングですね。決定したパラメータを含めた数式も表示されています。a = -0.2308、b = 253.28 ということですね（LibreOfficeの既定ではパラメータが10桁以上表示されるのですが、ここでは適度に丸めてあります）。
残差平方和を確認する
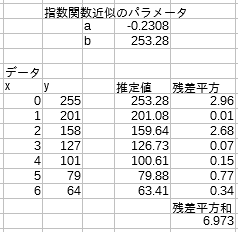
念のために残差平方和を求めておきます(図3)。この場合は、6.97 になりました。もしパラメータが最小二乗法で求められたとすると、これが残差平方和の最小値となるはずです。すなわち、パラメータをいろいろ変化させても、残差平方和がこれ以上小さくなることはない、ということです。
それも確認してみましょう。表計算ソフトにはソルバー（solver）という機能があり、特定のセルの値を最適化するようなパラメータの値を、数値計算的に求めることができます。使い方は付録に譲るとして、さっそくやってみましょう。
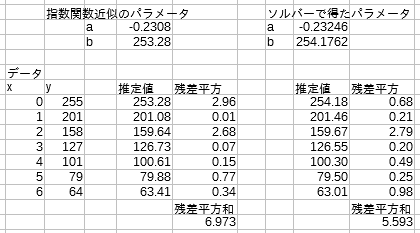
結果は図4のようになりました。はい、a = -0.2325、b = 254.18 というパラメータを与えることにより、残差平方和が 5.59 となります。これが本当に最小なのかは置いておくとしても、先に指数関数近似で得たパラメータは、残差平方和を最小にするものではないことがわかりました。どうしてこうなったのでしょうか…
ということで、後編に続きます。
付録：ソルバーの使い方
ここではソルバーのアルゴリズムについての説明は避けて、使い方だけを説明します。MS Excelでも同じような手順で使うことができるはずです（ソルバーアドインを読み込んでおく必要があるかもしれません）。
改めて今やりたいことを確認すると、2つのパラメータa、bをいろいろ動かして、残差平方和を最小にしたいのでした。
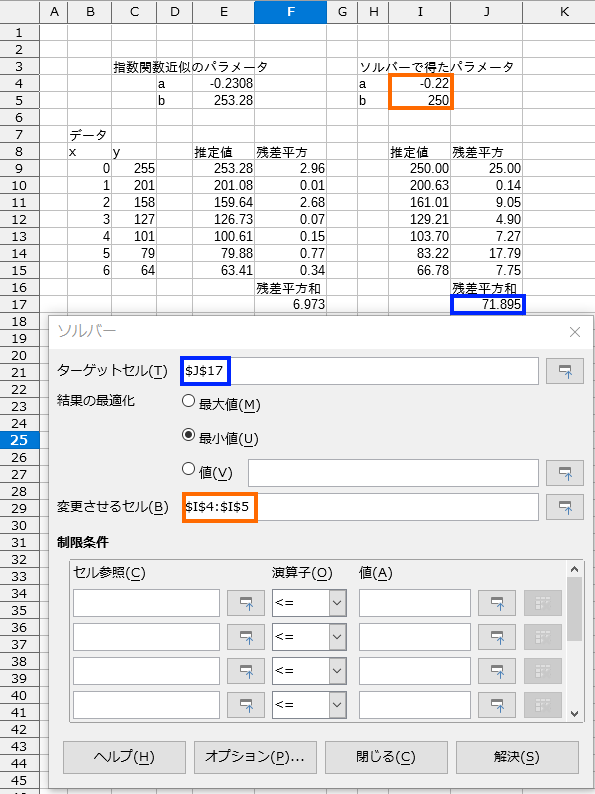
- メニューの[ツール] – [ソルバー]で、ソルバーダイアログ(図5)を開きます。
- [ターゲットセル]に残差平方和のセルを指定し、[結果の最適化]で[最小値]を選択します。
- [変更させるセル]には、パラメータaとbの入ったセルを選択します。それぞれのセルには、最低限にはそれらしい初期値を入れておくといいでしょう。
- [オプション]で[ソルバーエンジン]をいろいろイジることができますが、最小二乗法くらいであればデフォルト設定で問題ないでしょう。
あとは[解決]をクリックすると探索が始まり、停滞する（＝ある程度まともそうな値に収束する？）と[ソルバーの状態]ダイアログ(図6)が表示され、結果（ターゲットセルの最小値）を返してくれます。
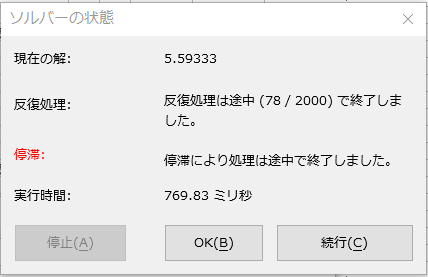
[続行]をクリックすると、探索を続行します。[OK]をクリックすると探索を終了し、得られたパラメータをシートに反映するかどうかを尋ねられます。