基礎物理学実験の題目「ばね振り子の振動」では、共振周波数を探し出し、それ(とおもりの質量)からばね定数を求めています。実験課題としてはそれだけなのですが、ばね定数を求める方法は(少なくとも)もう一つあることはみんなが知っているはずです。そう、ばねに対する荷重と伸びを測定する方法です。その測定をやってみた、という話になります。
目的
与えられたばね振り子のばね定数(spring constant)を測定します。ばね振り子は、おもりにばねを取り付けたものですが、そのばねのばね定数を測定する、ということです。
手順
- ばね振り子を吊り下げたときのばねの長さ l1 を測定する。
- ばね振り子からおもりを取り外してばねだけを吊り下げ、その自然長 l0 を測定する。
- ばね振り子のおもりの質量 m1 を測定する。
- ばねに、質量 m2 の物体を取り付けて吊り下げ、ばねの長さ l2 を測定する。
手順3までで、ばね定数を k = m1g / (l1 – l0) により求めることができます(gは重力加速度、ここでは 9.8026 m/s2とします。ちなみに、弘前大学理工学部1号館1階には日本重力基準網2016の基準重力点があり、重力値が 9.8026121 m/s2 と測定されています)。手順4は荷重とばねの伸びの直線性を確認するために行います。
測定結果
それでは手順に沿って進めていきます。
まずはばね振り子を吊り下げましょう。ここでは(チート対策として)学生実験で使っているものとは別の仕様のばねを使っています。

この状態でばねの下端と上端を読み取ります。どこまでをばねの長さとするかについてはいろいろ基準がありそうですが、ここでは上下のフック部を除いた各端間の長さと定義します。念のためそれぞれを真横から見た写真も用意しました。

下端はネジに隠れていますが、アダプターの上端と同じぐらいでしたのでそれを読み取ります。92.0 mm でしょうか。上端も評価が難しいですが、ここでは 220.5 mm とします。ばねの長さ l1 は 128.5 mm ですね。
続いて自然長の測定を行います。おもりを外してばねだけを吊り下げます。

下端は…ばねの前後でぶれがありますが、189.5 mm とします。自然長の上端を 220.5 mm と読み取り、自然長 l0 は 31.0 mm と求められました。

おもりの質量 m1 は、77.43 g でした。ちなみにばねの質量は 1.84 g です。おもりの中の磁石が電子天秤に悪影響を及ぼすため、段ボール箱に乗せて測定しています。もちろん、段ボール箱を乗せた状態でゼロ調整をしています。
ばねの質量はばね振り子の質量のうちの2%程度で、それを無視していいかどうかはきわどいところですが、ここでは無視できるものと考えておきます。
ここまでの測定値からばね定数を求めてみます。k = 77.43 g * 9.8026 m・s-2 / (128.5 mm – 31.0 mm) = 7.78 N/m となりました。gをkgに直す10-3とmmをmに直す10-3が、分子と分母でキャンセルするので、そのまま計算できますね!
最後に、おもりの代わりに手元にあった鍵をばねに取り付けて測定しましょう。


重心バランスの関係でばねが傾いているので、どこを下端とするか悩みますね。とりあえず手前と奥の平均をとることにしましょう。165.0 mm でしょうか。上端は相変わらず 220.5 mm ですので、ばねの長さ l2 は 55.5 mm となります。

そして鍵の質量 m2 は 26.57 g でした。もちろん、箱のない状態で改めてゼロ調整をしています。
結果と考察
荷重とばねの伸びの関係
| # | 荷重 / gw | ばねの長さ / mm | ばねの伸び / mm |
| 0 | 0 | 31.0 | 0 |
| 2 | 26.57 | 55.5 | 24.5 |
| 1 | 77.43 | 128.5 | 97.5 |
得られた測定結果をまとめると表1のようになり、それをグラフで表現したのが図1です。本来は独立変数である荷重を横軸にとるべきなのですが、ここでは傾きがばね定数に対応するわかりやすさを重視して、荷重を縦軸にとっています。
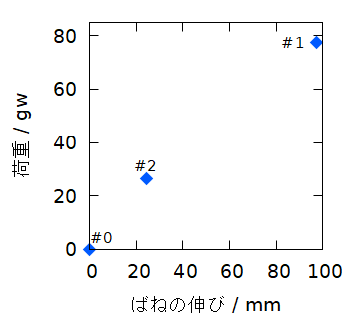
フックの法則に従うのならば、荷重(質量)とばねの伸びは比例するはずなのですが、図1のグラフからはそうなっていないことがわかります(#2の点のあたりで、上に凸になりそうですね!)。したがって上で求めた「ばね定数」kが意味をもつ値なのかどうかが怪しくなってきました。鍵を取り付けた振り子の長さの測定に起因するものと考えた受講者がいましたが、比例するには測定値があと 9 mm大きくなる必要があり、この測定がそこまで大きな誤差を含むとは考えにくいです。
共振周波数から求めたばね定数との比較
共振周波数から求めたばね定数との比較を行いましょう。共振周波数 f0 は 1.495 Hz と得られたので、それとおもりの質量 m1 = 77.43 g を使ってばね定数を求めると、k’ = m1 (2π・f0)2 = 6.85 N/m となります。
表1の#0と#1から求めたばね定数 7.78 N/m とは10%以上の差があります。この差はどこから来たのでしょうか?
ばね定数kは#0と#1の平均的な(大域的な)「ばね定数」ですが、k’は吊り下げた状態で測定した結果に基づいていますので、#1の周辺での(局所的な)「ばね定数」を求めていることになります。そのことが両者の差異を生んでいると考えられます。
kを、#1周辺での局所的な値に近づけるにはどうすればいいでしょうか?kを求めるときに#0の代わりに#2を使って、#1と#2の2点からばね定数を求めてみましょう(それを k*とします)。
k* = (77.43 g – 26.57 g) * 9.8026 m・s-2 / (97.5 mm – 24.5 mm) = 6.83 N/m となりました。
測定値(共振周波数やばねの伸び)が含む不確かさを考慮すると、これは共振周波数から求めたばね定数k’ = 6.85 N/m と一致すると言えます。つまり#2から#1の荷重の範囲では、ばねの荷重と伸びに直線的な関係があると推測されます。
まとめ
ばね振り子のばね定数は、異なる荷重によるばねの長さから、6.85 N/m と求められました。これは、共振周波数から求めたばね定数 6.83 N/m と一致し、ある程度の荷重の範囲では直線的な荷重-伸び特性を示すものと推測されます。一方で無荷重(自然長)付近では、より伸びにくいことが確認されました。
もう少し種明かしをすると、ここで使われているばねは引張コイルばねというタイプのもので、ある一定以下の荷重ではばねの長さが変わらないという性質があります。その荷重を初張力と言いますが、初張力より大きな荷重を受けるとばねの伸びは荷重に対して直線的に変化します[2]。#0と#1から求めたばね定数 k が k’ や k* より大きな値になったのは、初張力の影響によるものであると考えられます。
余談
本記事は、(メディア授業として行われた)2020年度の数物科学科「基礎物理学実験I」向けの補助コンテンツとして私が提供したものをもとに再構成したものです。補助コンテンツ内では測定値のみを提供し、考察の方向性(あるいはそもそも考察に援用するか否か)は受講者に委ねました。そのコンテンツでは、共振周波数から求めた共振周波数(ならびにばね定数)の妥当性を確認するために別の方法でばね定数を測定する、という動機付けをしていたと思います。当時は3分の1程度の受講者がそのコンテンツを援用した考察を行っていましたが、「#1と#2の測定値からばね定数を求める」ところにたどり着いた受講者はいなかったと記憶しています。
また、ある種のばねについての初張力という概念については、私自身も補助コンテンツ作成時の調査で初めて知りました。こういうコンテンツを作成していなければ、今も知る機会はないままだったと思います。
参考サイト
- バネ振り子の周期 : MAkasaka’s Homepageの「高校ぶつり実験」より。本記事と同じような実験を行っています(高校物理の授業で行っているのでしょうか)。実験Iでグラフの切片が正であること、実験IIの相対誤差がmが増えるにつれて小さくなっていることから、質量にオフセットがある(ばね自身の質量?)ことが実験IIの相対誤差の主要因だと思いましたが、どうでしょう?
- 引張コイルばねの特徴と種類 : モノタロウの「機械要素の基礎講座」より。引張コイルばねや初張力について解説しています。