「ケプラー方程式を数値的に解いてケプラーの第2法則を視覚的に確認する」の内容を,逐次近似解を使い,draw2d() で解く例。
ケプラー方程式
楕円の焦点を原点としたデカルト座標 $x, y$ は媒介変数 $u$ (離心近点離角)によって,時間 $t$ と関係づけられているが,$t$ の陽関数としては表すことができない。
\begin{eqnarray}
x &=& r \cos\varphi = a(\cos u – e)\\
y &=& r \sin\varphi = a \sqrt{1-e^2} \sin u\\
\frac{2\pi}{T} t &=& u – e \sin u
\end{eqnarray}
上記の3行目の式を $\omega \equiv \frac{2\pi}{T}$ として
$$u – e \sin u= \omega t$$
と書いた式が,離心近点離角 $u$ と時間 $t$ を関係付ける ケプラー方程式 である。
逐次近似法によるケプラー方程式の逐次近似解
離心率 $e$ は $0 \leq e < 1$ であることから,ケプラー方程式
$$u – e \sin u = \omega t$$
を以下のように逐次近似的に解いてみます。
\begin{eqnarray}
u &=& \omega t + e \sin u \\
u_0 &=& \omega t\\
u_1 &=& \omega t + e \sin u_0 = \omega t + e \sin \omega t\\
u_2 &=& \omega t + e \sin u_1 =\omega t + e \sin\left(\omega t + e \sin \omega t\right) \\
u_3 &=& \omega t + e \sin u_2 =\omega t + e \sin\left\{\omega t + e \sin\left(\omega t + e \sin \omega t\right)\right\} \\
&\vdots&\\
u_{n} &=& \omega t + e \sin u_{n-1} = \dots\\
\end{eqnarray}
$n$ が大きくなると,入れ子になっている項がどんどん増殖していきますが,$u_3$ のあたりまでは,近似的に $u$ は $t$ の陽関数としてあらわされているなぁ… という見た目がします。
上の式にそって,以下のように関数 $u(n, e, \omega t)$ を再帰的に定義します。
u(N, e, omegat):=
block(
if N = 0 then
omegat
else
omegat + e*sin(u(N-1, e, omegat))
)$
/* たとえば n = 3 のときは... */
u3 = u(3, e, omega * t);
$u(\omega t)$ を使えば,天体の位置 $x, \ y$ が $t$ のあからさまな関数(陽関数)として表すことができます。$N = 10$ としておきます。($N$ をどれくらいにするかは,逐次近似の精度をどの程度にするかによります。各自精度のチェックをすること。)
\begin{eqnarray}
x(\omega t) &=& a (\cos u(\omega t) – e) \\
y(\omega t) &=& a \sqrt{1-e^2} \sin u(\omega t)
\end{eqnarray}
x(a, e, omegat):= a*(cos(u(10, e, omegat)) - e);
y(a, e, omegat):= a*sqrt(1-e**2)*sin(u(10, e, omegat));
/* omega t の範囲 [0, 2 π] を Ndiv 等分して
天体の位置 [x, y] のリストを作成する */
Ndiv: 36$
pi: float(%pi)$
pxy: makelist([x(5, 0.6, 2*pi/Ndiv * i), y(5, 0.6, 2*pi/Ndiv * i)], i, 0, Ndiv+1)$
/* draw2d() でオプションを設定してグラフを描く */
draw2d(
/* 滑らかに曲線を描くように */
nticks = 300,
/* 表示範囲 */
xrange = [-9, 3], yrange = [-6, 6],
/* 縦横比。*/
proportional_axes = xy,
/* x 軸 y 軸の表示 */
xaxis = true, yaxis = true,
/* 軸のきざみ目盛の非表示 */
xtics = false, ytics = false,
/* 横軸縦軸のラベル */
xlabel = "x", ylabel = "y",
/* 楕円軌道 */
line_width = 1,
color = red,
parametric(x(5, 0.6, omegat), y(5, 0.6, omegat), omegat, 0, 2*%pi),
/* 2点をむすぶ直線を描く例 */
point_type = none,
line_type = dots,
color = black,
points_joined = true,
points([[0, 0],pxy[2]]),
points([[0, 0],pxy[18]]),
points([[0, 0],pxy[20]]),
points([[0, 0],pxy[36]]),
points_joined = false,
/* 点を打つ例 */
point_type = 7,
point_size = 1,
color = blue,
points(pxy),
/* 原点 */
point_type = 7,
point_size = 1,
color = black,
points([[0, 0]])
)$
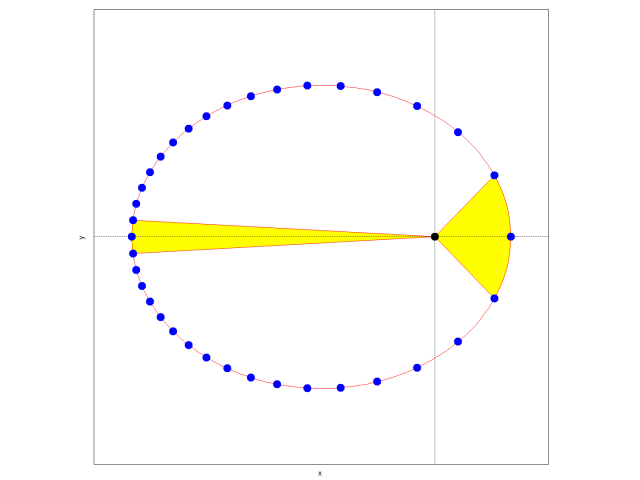
上の図から,一定時間間隔ごとの位置のプロットなのに,原点(焦点)に近いときは間隔が広い,つまりすばやく動き,原点から離れているときは感覚が狭い,つまりゆっくり動いていることがわかる。
原点の右側,近点付近の扇形の面積と,原点の左側,遠点付近の扇形の面積は等しい。
/* 現在のグラフをファイルに保存。*/
/* 弘大 JupyterHub では
set_draw_defaults(file_name="~/.maxplot",terminal='svg)$
されているので。*/
system("cp ~/.maxplot.svg ./draw-kep.svg")$
パラパラアニメをつくる
各時刻ごとの画像を %03d.png のようにファイルとして保存し,(弘大 JupyterHub にインストールされている ffmpeg を使って)ファイル名 out.mp4 の動画ファイルを作成する。
/* バリエーション 1 */
for i:1 thru Ndiv do(
/* %03d.png のような filename にしたい。*/
tmpname: printf(false, "~4d",1000+i),
filename: substring(tmpname, 2),
draw2d(
/* 滑らかに曲線を描くように */
nticks = 300,
/* 表示範囲 */
xrange = [-9, 3], yrange = [-6, 6],
/* 縦横比。*/
proportional_axes = xy,
/* x 軸 y 軸の表示 */
xaxis = true, yaxis = true,
/* 軸のきざみ目盛の非表示 */
xtics = false, ytics = false,
/* 横軸縦軸のラベル */
xlabel = "x", ylabel = "y",
/* 楕円軌道 */
line_width = 1,
color = red,
parametric(x(5, 0.6, omegat), y(5, 0.6, omegat), omegat, 0, 2*%pi),
/* 点を打つ例 */
point_type = 7,
point_size = 3,
color = blue,
points([pxy[i]]),
/* 原点 */
point_type = 7,
point_size = 3,
color = black,
points([[0, 0]]),
/* 各 i ごとに png ファイルに保存する。*/
file_name = filename,
dimensions = 120*[12.0,9.0],
terminal = png
)
)$
/* バリエーション 2 */
for i:1 thru Ndiv do(
/* %03d.png のような filename にしたい。*/
tmpname: printf(false, "~4d",1000+Ndiv+i),
filename: substring(tmpname, 2),
draw2d(
/* 滑らかに曲線を描くように */
nticks = 300,
/* 表示範囲 */
xrange = [-9, 3], yrange = [-6, 6],
/* 縦横比。*/
proportional_axes = xy,
/* x 軸 y 軸の表示 */
xaxis = true, yaxis = true,
/* 軸のきざみ目盛の非表示 */
xtics = false, ytics = false,
/* 横軸縦軸のラベル */
xlabel = "x", ylabel = "y",
/* 楕円軌道 */
line_width = 1,
color = red,
parametric(x(5, 0.6, omegat), y(5, 0.6, omegat), omegat, 0, 2*%pi),
/* 点を打つ例 */
point_type = 7,
point_size = 3,
color = blue,
points(firstn(pxy, i)),
/* 原点 */
point_type = 7,
point_size = 3,
color = black,
points([[0, 0]]),
/* 各 i ごとに png ファイルに保存する。*/
file_name = filename,
dimensions = 120*[12.0,9.0],
terminal = png
)
)$
/* バリエーション 3 */
for i:2 thru Ndiv+1 do(
/* %03d.png のような filename にしたい。*/
tmpname: printf(false, "~4d",1000+2*Ndiv+i-1),
filename: substring(tmpname, 2),
draw2d(
/* 滑らかに曲線を描くように */
nticks = 300,
/* 表示範囲 */
xrange = [-9, 3], yrange = [-6, 6],
/* 縦横比。*/
proportional_axes = xy,
/* x 軸 y 軸の表示 */
xaxis = true, yaxis = true,
/* 軸のきざみ目盛の非表示 */
xtics = false, ytics = false,
/* 横軸縦軸のラベル */
xlabel = "x", ylabel = "y",
/* 楕円軌道 */
line_width = 1,
color = red,
parametric(x(5, 0.6, omegat), y(5, 0.6, omegat), omegat, 0, 2*%pi),
/* 2点をむすぶ直線を描く例 */
point_type = none,
color = red,
points_joined = true,
points([[0, 0],pxy[i-1]]),
points([[0, 0],pxy[i]]),
points_joined = false,
/* 点を打つ例 */
point_type = 7,
point_size = 3,
color = blue,
points(pxy),
/* 原点 */
point_type = 7,
point_size = 3,
color = black,
points([[0, 0]]),
/* 各 i ごとに png ファイルに保存する。*/
file_name = filename,
dimensions = 120*[12.0,9.0],
terminal = png
)
)$
楕円の式
$$\frac{(x + a e)^2}{a^2} + \frac{y^2}{b^2} = 1$$
より,$y$ を $x$ の陽関数として表して
\begin{eqnarray}
y = \pm b \sqrt{1 – \frac{(x + a e)^2}{a^2}} = \pm a \sqrt{1-e^2} \sqrt{1 – \frac{(x + a e)^2}{a^2}}
\end{eqnarray}
yp(a, e, x):= a*sqrt(1-e**2)*sqrt(1 - (x+a*e)**2/a**2);
ym(a, e, x):= -yp(a, e, x);
/* 扇形を塗りつぶし */
/* %03d.png のような filename にしたい。*/
tmpname: printf(false, "~4d",1000+3*Ndiv+1)$
filename: substring(tmpname, 2)$
draw2d(
/* グリッドや座標軸が塗りつぶされないように */
user_preamble = "set grid front;",
/* 滑らかに曲線を描くように */
nticks = 300,
/* 表示範囲 */
xrange = [-9, 3], yrange = [-6, 6],
/* 縦横比。*/
proportional_axes = xy,
/* x 軸 y 軸の表示 */
xaxis = true, yaxis = true,
/* 軸のきざみ目盛の非表示 */
xtics = false, ytics = false,
/* 横軸縦軸のラベル */
xlabel = "x", ylabel = "y",
/* 塗りつぶす色の指定。*/
fill_color = yellow,
/* 近点側 */
/* 上の線。y = f(x) を filled_func に代入。*/
filled_func = pxy[2][2]/pxy[2][1]*x,
/* 下の線。y = g(x) を 0 < x < 2 の範囲で描く。*/
explicit(-pxy[2][2]/pxy[2][1]*x, x, 0, pxy[2][1]),
/* 上の線。y = f(x) を filled_func に代入。*/
filled_func = yp(5, 0.6, x),
/* 下の線。y = g(x) を 0 < x < 2 の範囲で描く。*/
explicit(ym(5, 0.6, x), x, pxy[2][1], pxy[1][1]),
/* 遠点側 */
/* 上の線。y = f(x) を filled_func に代入。*/
filled_func = pxy[18][2]/pxy[18][1]*x,
/* 下の線。y = g(x) を 0 < x < 2 の範囲で描く。*/
explicit(-pxy[18][2]/pxy[18][1]*x, x, pxy[18][1], 0),
/* 上の線。y = f(x) を filled_func に代入。*/
filled_func = yp(5, 0.6, x),
/* 下の線。y = g(x) を 0 < x < 2 の範囲で描く。*/
explicit(ym(5, 0.6, x), x, pxy[19][1], pxy[18][1]),
/* 塗りつぶし終了。*/
filled_func = false,
/* 楕円軌道 */
line_width = 1,
color = red,
parametric(x(5, 0.6, omegat), y(5, 0.6, omegat), omegat, 0, 2*%pi),
/* 2点をむすぶ直線を描く例 */
point_type = none,
color = red,
points_joined = true,
points([[0, 0],pxy[2]]),
points([[0, 0],pxy[36]]),
points([[0, 0],pxy[18]]),
points([[0, 0],pxy[20]]),
points_joined = false,
/* 点を打つ例 */
point_type = 7,
point_size = 3,
color = blue,
points(pxy),
/* 原点 */
point_type = 7,
point_size = 3,
color = black,
points([[0, 0]]),
/* png ファイルに保存する。*/
file_name = filename,
dimensions = 120*[12.0,9.0],
terminal = png
)$/* 古い out.mp4 は削除してから。*/
system("rm -f out.mp4")$
/* framerate を変えるとパラパラアニメの速さがかわる。*/
/* stream_loop はさらに何回繰り返すかを指定する。*/
system("ffmpeg -hide_banner -loglevel error -stream_loop 0 -framerate 10 -i %03d.png -vcodec libx264 -pix_fmt yuv420p out.mp4")$
system("rm -f ???.png")$