特殊相対論においては，光源・観測者間の相対速度がゼロの瞬間であっても，観測される光の振動数の変化が起こる。特殊相対論特有のこの効果は「横ドップラー効果」と呼ばれる。横ドップラー効果の原因としては，光源の時間の進み方が特殊相対論的効果によって遅れるからだ，などという説明があるが…
観測者が動く場合
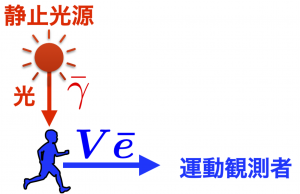
光源が静止し，観測者が運動する場合を例に，別ページに書いた内容をおさらいすると，光源静止系での振動数を \(\omega_0\) ，運動する観測者が測定する振動数を \(\omega_{\rm obs}\) と表記すると
$$\omega_{\rm obs} = \omega_0 \frac{\sqrt{1-V^2}}{1+V \cos\bar{\theta}}$$
横ドップラー効果とは，観測者にとって真横 $\displaystyle \bar{\theta} = \frac{\pi}{2}$ からくる光に対して
$$ \omega_{\rm obs} = \omega_0 {\sqrt{1-V^2}} < \omega_0$$
となり，光源・観測者間の相対速度はこの瞬間ゼロ（光源に向かうあるいは離れる速度成分がゼロ）であるが，振動数の変化が起こる現象である。
この横ドップラー効果が起こった状況を，光源静止系でみると，どうなるか。
「光行差」のページで導いたように，光源静止系でみた時の光の角度 $\theta$ は $\bar{\theta}$ と以下のような関係がある。
$$\cos \bar{\theta} = \frac{\cos\theta -V}{1 – V\cos\theta} \tag{1}$$
従って $\displaystyle \cos\bar{\theta} = \cos\frac{\pi}{2} = 0$ の時の $\theta$ は
$$\cos\theta = V, \quad \therefore\ \ 0 < \theta < \frac{\pi}{2} $$
となる。
光の入射角 $\varTheta = \pi – \theta$ で表すと
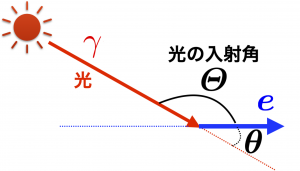
$$ \frac{\pi}{2} < \varTheta < \pi$$
となり，光源静止系からみると「横ドップラー効果」を起こしている光は運動観測者の後方から入射していると見える。
「真横」からの光ではなくて，後方からの光を遠ざかりながら見ているのだから，ドップラー効果で振動数が小さくなるのは当然だよね，ということになる。
光源が動く場合
$$\omega_{\rm obs} = \omega_0 \frac{\sqrt{1-V^2}}{1-V \cos{\theta}}$$
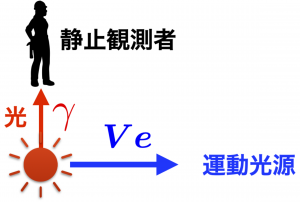
観測者にとって真横 $\displaystyle {\theta} = \frac{\pi}{2}$ からくる光に対して
$$ \omega_{\rm obs} = \omega_0 {\sqrt{1-V^2}} < \omega_0$$
となり，光源・観測者間の相対速度はこの瞬間ゼロであるが，振動数の変化が起こる。
これを光源静止系でみると，$\displaystyle \cos{\theta} = \cos\frac{\pi}{2} = 0$ の時の $\bar{\theta}$ は $(1)$ 式から
$$\cos\bar{\theta} = -V, \quad \therefore\ \ \bar{\theta} > \frac{\pi}{2} $$
となる。
光の入射角 $\bar{\varTheta} = \pi – \bar{\theta}$ で表すと
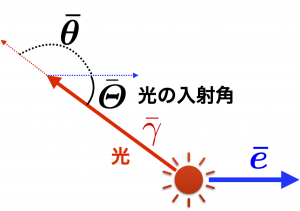$$ 0< \bar{\varTheta} < \frac{\pi}{2}$$
となり，光源静止系からみると「横ドップラー効果」を起こしている光は，運動光源が観測者から遠ざかりながら放出した光が観測者に届いていると見える。
「真横」からの光ではなくて，遠ざかる光源からの光を見ているのだから，ドップラー効果で振動数が小さくなるのは当然だよね，ということになる。
教訓：
観測者からみて「真横」でも，光源静止系では「真横」ではない。まあ，こういう見方もできる，ということで。