世の中の教科書による標準的な説明では,光源あるいは観測者の運動による光のドップラー効果は,重力がない場合の特殊相対論的状況でのみ有効であるローレンツ変換を用いて説明されていた。重力がある場合は,ローレンツ変換が成り立たないため,別途理屈を考える必要があるのであった。
一方で,重力赤方偏移の標準的な説明は,重力場中において光源も観測者も静止している場合にのみ有効であった。
では,重力場中を運動する観測者の観測する光の振動数(や波長)を調べるにはどうすればよいか?
ここでは,赤方偏移を統一的に理解する方法に従って,
I. 重力場中の光の伝播は,ヌル測地線で与えられる
II. 4元速度 $u^{\mu}$ の観測者が観測する光の振動数は $\omega = – k_{\mu} u^{\mu}$ で与えられる
という2つの原理原則から,シュバルツシルト時空中を動径方向に自由落下運動する観測者が観測する光のドップラー効果の式を導く。
シュバルツシルト時空中を動径方向に伝播する光
光の4元波数ベクトルを $k^{\mu}$ とすると,動径方向に伝播することから
$$k^{\mu} = (k^0, k^1, 0, 0)$$
測地線方程式は別ページ「シュバルツシルト時空中の光の伝播」で解いているから,その結果を使うと,$k_{\mu} = g_{\mu\nu} \,k^{\nu}$ について
$$k_{\mu} = \left(k_0, k_1, 0, 0 \right) = \left(-\omega_c, \ \pm \frac{\omega_c}{1 – \frac{r_g}{r}}, \ 0, \ 0 \right)$$
複号 \(\pm\) は,動径方向外向きに伝播する光に対してプラス,内向きの光に対してマイナスをとる。
シュバルツシルト時空中の静止観測者
静止観測者の4元速度 $u^{\mu}$ は
$$u^{\mu} = \left(u^0, 0, 0, 0\right) = \left(\frac{1}{\sqrt{1 – \frac{r_g}{r}}}, 0, 0, 0\right)$$
静止観測者が観測する光の振動数は
$$\omega = – k_{\mu} u^{\mu} = – k_{0} u^{0} = \frac{\omega_c}{\sqrt{1 – \frac{r_g}{r}}}$$
$r = r_1$ の光源から振動数 $\omega_1$ で放出された光を,離れた位置 $r\ (> r_1)$ で観測した時の振動数を $\omega$ とすると,
$$\frac{\omega}{\omega_1} = \frac{\sqrt{1 – \frac{r_g}{r_1}}}{\sqrt{1 – \frac{r_g}{r}}} < 1 \quad (r_g < r_1 < r)$$
これが,静止観測者が観測する重力赤方偏移。
シュバルツシルト時空中を動径方向に自由落下運動する観測者
シュバルツシルト時空中を動径方向に自由落下運動する観測者の4元速度 $\bar{u}^{\mu}$ は,別ページ「シュバルツシルト時空中を動径方向に自由落下運動する観測者」で計算したように,$r = r_i\ (> r)$ で静止しているという初期条件を課すと,
$$\bar{u}^{\mu} = \left(\frac{ \sqrt{1 – \frac{r_g}{r_i}}}{1 – \frac{r_g}{r}}, -\sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}}, 0, 0\right) $$
この運動する観測者が観測する動径方向外向きに放出された光の振動数 $\bar{\omega}$ は
\begin{eqnarray}
\bar{\omega} &=& – k_{\mu} \bar{u}^{\mu} \\
&=& – k_0 \bar{u}^0 – k_1 \bar{u}^1 \\
&=& \omega_c \frac{ \sqrt{1 – \frac{r_g}{r_i}}}{1 – \frac{r_g}{r}} \pm \frac{\omega_c}{1 – \frac{r_g}{r}} \sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}} \\
&=& \frac{\omega_c}{1 – \frac{r_g}{r}} \left(\sqrt{1 – \frac{r_g}{r_i}} \pm \sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}}\right)
\end{eqnarray}
重力場中を運動する観測者によるドップラー効果
観測者が光源に近づく場合
自由落下運動する観測者が光源に近づく場合は,下図のように $r_g < r_1 < r< r_i$ となり,光は外向き,つまり複号 \(\pm\) の \(+\) をとる。
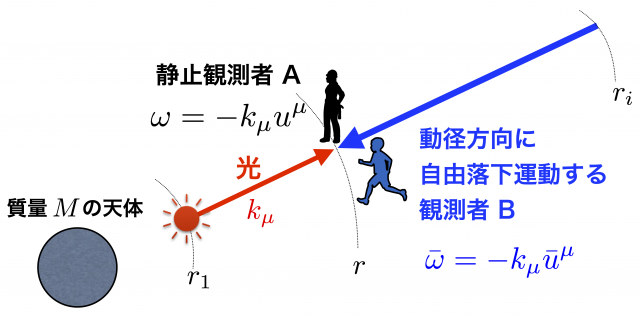
したがって,$r = r_1$ の光源から振動数 $\omega_1$ で放出された同じ光を,離れた位置 $r\ (> r_1)$ で静止観測者が観測する場合と,自由落下運動する観測者が観測する場合とでは,
\begin{eqnarray}
\frac{\frac{\bar{\omega}}{\omega_1}}{\frac{{\omega}}{\omega_1}} &=& \frac{\bar{\omega}}{\omega} \\
&=& \frac{1}{\sqrt{1 – \frac{r_g}{r}}} \left(\sqrt{1 – \frac{r_g}{r_i}} + \sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}}\right) > 1
\end{eqnarray}
となり,自由落下運動して $r = r_1$ にある光源に近づいていく観測者が観測する振動数 $\bar{\omega}$ のほうが,静止観測者の観測する振動数 $\omega$ よりドップラー効果によって大きくなることがわかる。
特に,観測者が十分遠方から自由落下運動をはじめたとすると,\(r_i \rightarrow \infty\) として
$$\frac{\bar{\omega}}{\omega} \simeq \frac{1 + \sqrt{\frac{r_g}{r} }}{\sqrt{1 – \frac{r_g}{r}}}$$
念のため,この不等式の証明。
\begin{eqnarray}
\frac{\sqrt{1 – \frac{r_g}{r_i}} + \sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}}}{\sqrt{1 – \frac{r_g}{r}}} &>&
\frac{\sqrt{1 – \frac{r_g}{r_i}} }{\sqrt{1 – \frac{r_g}{r}}}\\
&=& \frac{\sqrt{1 – \frac{r_g}{r} + \left( \frac{r_g}{r} – \frac{r_g}{r_i}\right)} }{\sqrt{1 – \frac{r_g}{r}}} \\
&>& \frac{\sqrt{1 – \frac{r_g}{r} } }{\sqrt{1 – \frac{r_g}{r}}} \\
&=& 1 \\ \ \\
\therefore\ \ \frac{\sqrt{1 – \frac{r_g}{r_i}} + \sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}}}{\sqrt{1 – \frac{r_g}{r}}} &>& 1
\end{eqnarray}
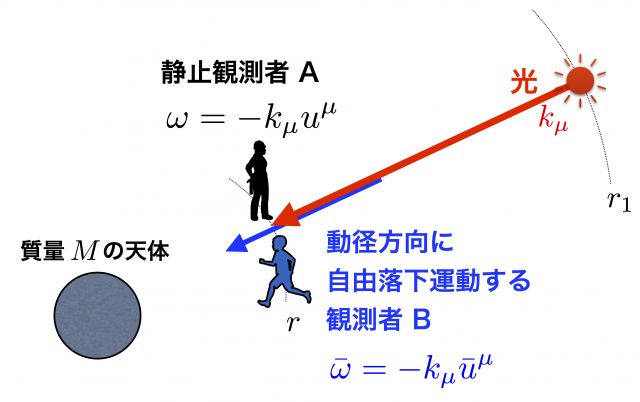
観測者が光源から遠ざかる場合
逆に,自由落下運動する観測者が光源から遠ざかる場合は,下図のように $r_g < r < r_1, \ \ r < r_i$ となり,光は内向き,つまり複号 \(\pm\) の \(-\) をとる。
\begin{eqnarray}
\frac{\bar{\omega}}{\omega}
&=& \frac{1}{\sqrt{1 – \frac{r_g}{r}}} \left(\sqrt{1 – \frac{r_g}{r_i}} – \sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}}\right) \\
&=& \frac{\left(\sqrt{1 – \frac{r_g}{r_i}} – \sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}}\right)\left(\sqrt{1 – \frac{r_g}{r_i}} + \sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}}\right)}{\sqrt{1 – \frac{r_g}{r}}\left(\sqrt{1 – \frac{r_g}{r_i}} + \sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}}\right)} \\
&=& \frac{\left(1 – \frac{r_g}{r_i}\right) – \left(\frac{r_g}{r} – \frac{r_g}{r_i}\right)}{\sqrt{1 – \frac{r_g}{r}}\left(\sqrt{1 – \frac{r_g}{r_i}} + \sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}}\right)} \\
&=& \frac{\sqrt{1 – \frac{r_g}{r}}}{\sqrt{1 – \frac{r_g}{r_i}} + \sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}}} < 1
\end{eqnarray}
となり,光源から遠ざかる場合にはドップラー効果により,静止観測者が観測する振動数よりも小さくなることがわかる。
特に,観測者が十分遠方から自由落下運動をはじめたとすると,\(r_i \rightarrow \infty\) として
$$\frac{\bar{\omega}}{\omega} \simeq \frac{1 – \sqrt{\frac{r_g}{r} }}{\sqrt{1 – \frac{r_g}{r}}} = \frac{\sqrt{1 – \frac{r_g}{r}}}{1 + \sqrt{\frac{r_g}{r} }}$$
光のドップラー効果の式との整合性
さて,本サイトでは「ローレンツ変換によらない赤方偏移の統一的理解」において,光のドップラー効果の式は,(特殊相対論でのみ有効な)ローレンツ変換を使わずに求めることができることを示している。
光源に近づく場合の光のドップラー効果の式
特に,光源静止系での振動数 \(\omega\) を \(\omega_0\) ,運動する観測者が測定する振動数 \( \bar{\omega}\) を \(\omega_{\rm obs}\) と表記すると,観測者が3次元的な速さ $V$ で光源に近づく場合の光のドップラー効果の式
$$ \omega_{\rm obs} = \omega_0 \sqrt{\frac{1+V}{1-V} } $$
は,特殊相対論的状況のみならず,その導出方法の一般性から重力がある一般相対論的な状況においても同様に有効である。
動径方向に自由落下運動する観測者の3次元的速さ $V$
動径座標 $r$ の地点の静止観測者 $A$ からみると,目の前を通過する瞬間の自由落下運動する観測者 $B$ の速さ $V$ は,「シュバルツシルト時空中を動径方向に自由落下運動する観測者」に記載のように,4元速度の合成則
$$\bar{u}^{\mu} = \frac{1}{\sqrt{1 – V^2}} u^{\mu} + \frac{V}{\sqrt{1 – V^2}} e^{\mu} $$
を使うと,それぞれの4元速度の内積がローレンツ因子を表すこと
$$\frac{1}{\sqrt{1-V^2}} = – u_{\mu} \bar{u}^{\mu}$$
から $V$ を求めることができ,
\begin{eqnarray}
V &=& \frac{ \sqrt{ \frac{r_g}{r} – \frac{r_g}{r_i} } }{ \sqrt{1-\frac{r_g}{r_i}} }
\end{eqnarray}
となる。
ドップラー効果の式に代入して…
上記の $V$ をドップラー効果の式に代入すると,
\begin{eqnarray}
\frac{\omega_{\rm obs}}{ \omega_0} &=& \sqrt{\frac{1+V}{1-V} } \\
&=& \frac{1+V}{\sqrt{1-V^2}} \\
&=& \frac{1+\frac{ \sqrt{ \frac{r_g}{r} – \frac{r_g}{r_i} } }{ \sqrt{1-\frac{r_g}{r_i}} }}{\sqrt{1-\frac{ { \frac{r_g}{r} – \frac{r_g}{r_i} } }{{1-\frac{r_g}{r_i}} }}}\\
&=&\frac{{ \sqrt{1-\frac{r_g}{r_i}} }+{ \sqrt{ \frac{r_g}{r} – \frac{r_g}{r_i} } }}{\sqrt{{{1-\frac{r_g}{r_i}} }-{ { \left(\frac{r_g}{r} – \frac{r_g}{r_i}\right) } }}}\\
&=&\frac{{ \sqrt{1-\frac{r_g}{r_i}} }+{ \sqrt{ \frac{r_g}{r} – \frac{r_g}{r_i} } }}{\sqrt{{{1-\frac{r_g}{r}} }}}
\end{eqnarray}
となり,(当然の結果ではあるが)上記で求めた $\displaystyle \frac{\bar{\omega}}{\omega}$ と一致している。
光源から遠ざかる場合も同様
速さ $V$ で光源から遠ざかる場合も同様で,
$$ \omega_{\rm obs}= \omega_0 \sqrt{\frac{1-V}{1+V} }$$
に速さ $V$ を代入すればよい。