Return to Python でコンピュータ演習（旧版アーカイブ）

SymPy で微分積分・方程式の解

Python および SymPy の基本から，関数，微分・積分，方程式の解まで。

弘大 JupyterHub での Python の起動

新しく Python で計算をはじめるときは，弘大 JupyterHub にログイン後，メニュー右端の「新規」から「Python 3」を選択します

JupyterHub での計算の実行と行末記号

  1. Python では，セルに実行文を書き，
  2. Shift キーを押しながら Enter キー（Return キー）を押すと実行します。
  3. Shift + Enter のかわりに，メニューの「▶︎ Run」をクリックしてもよいです。
  4. 行末にセミコロン ; を入力後，実行すると，結果が表示されません。

まずは簡単なかけ算 123×456 を計算してみます。

In [1]:
123 * 456
Out[1]:
56088

2 の 100 乗 ($2^{100}$) のような大きい数でも，厳密な結果を出力します。（** は累乗を表します。）

In [2]:
2**100
Out[2]:
1267650600228229401496703205376

float 関数を使って浮動小数点表示で近似値を出力させることもできます。

In [3]:
float(2**100)
Out[3]:
1.2676506002282294e+30

SymPy の import

Python 本体のみでできることは限られています。これからは，微分・積分などの記号計算を行うためのライブラリ SymPy が必要です。以下のようにして import しておきます。

In [4]:
from sympy.abc import *
from sympy import *

表記などの約束事

Python の実行に際して，いくつか表記についての約束事があります。代表的なものを以下に示します。

コメント (実行に影響しない注釈) を入れたいときは，# を書きます。

In [5]:
1 + 2 + 3
Out[5]:
6
In [6]:
1 + 2 # + 3
Out[6]:
3

加法 +，減法 -，乗法 *，除法 / における優先順位は数学と同じです。優先して計算したい箇所は ( ) で 囲みます。

In [7]:
1 + 2 * 3
Out[7]:
7
In [8]:
(1 + 2) * 3
Out[8]:
9

代入

変数に式や値を代入するときは，等号 = を使います。

変数 a に $100+3/21$
を代入し，a の値を表示させる例です。

In [9]:
a = 100 + 3/21
In [10]:
(a - 100) * 7
Out[10]:
0.9999999999999716

上記の計算では，割り算 / は実数になります。有理数として分数をあつかう際は，SymPy の Rational() を使います。

In [11]:
a = 100 + Rational(3,21)
a
Out[11]:
$\displaystyle \frac{701}{7}$
In [12]:
(a - 100) * 7
Out[12]:
$\displaystyle 1$

関数の定義

Python の記法で関数を定義します。$ f(x) = x^2$

In [13]:
def f(x):
    return x**2
In [14]:
f(x)
Out[14]:
$\displaystyle x^{2}$

$f(4) = 4^2 = 16$

In [15]:
f(4)
Out[15]:
16

実行結果の表示・非表示

上の例でわかるように，代入や関数の定義のときは，式や変数の値が表示されません。

In [16]:
eq = x**2 + 3*x + 2

明示的に変数を Shift + Enter すれば表示されますが，文末に ; をつけると結果が出力されません。

In [17]:
eq
Out[17]:
$\displaystyle x^{2} + 3 x + 2$
In [18]:
eq;

前の出力結果の参照

直前の出力結果は _ で参照できます。expand() は展開する関数です。

In [19]:
expand((x - 2)**4)
Out[19]:
$\displaystyle x^{4} – 8 x^{3} + 24 x^{2} – 32 x + 16$

直前の結果を factor() で因数分解します。

In [20]:
factor(_)
Out[20]:
$\displaystyle \left(x – 2\right)^{4}$

数の計算・基本的な関数

基本的な四則演算 (+ - * /) 以外によく使われる演算を示します。累乗は ** でした。

$4$ の階乗の計算をします。$4!=4×3×2×1=24$ です。SymPy では，階乗は factorial() 関数を使います。

In [21]:
factorial(4)
Out[21]:
$\displaystyle 24$

factorial2() 関数は，一つおきの階乗の計算をします。$5!!=5×3×1=15$ です。

In [22]:
factorial2(5)
Out[22]:
$\displaystyle 15$

練習 1-1

(練習) 3, 2, 1 でつくる最大の数

数字の 3 と 2 と 1 を 1 個ずつ使った演算でつくることができる最大の整数は?

ヒント:

(1 + 2) × 3 = 9 じゃ全然だめ。そのまま並べると 321 ですが，累乗を使うともっと大きい数をつくることができます。
$21^3$ とか，$31^2$ とか，$2^{31}$ とか…

In [ ]:
In [ ]:
In [ ]:
In [ ]:

基本的な定数

SymPy の基本的定数は，以下のようにして import しています。

from sympy import I, pi, E
　円周率 $\pi$　無限大 $\infty$　自然対数の底 $e$　虚数単位 $i$
piooEI

無限大は小文字の o（オー）を2つ並べて書きます。

無理数 $e$，$\pi$ と虚数単位 $i$ と整数 $−1$ の間のすてきな関係，オイラーの等式 $$e^{i\pi} +1 = 0$$

In [23]:
E**(I * pi) + 1
Out[23]:
$\displaystyle 0$

浮動小数点で近似値を表示するには float() を使います。

In [24]:
pi
Out[24]:
$\displaystyle \pi$
In [25]:
float(pi)
Out[25]:
3.141592653589793

基本的な関数

　平方根　指数関数　自然対数　絶対値　三角関数　逆関数　双曲線関数
sqrtexplogabssin
cos
tan		asin
acos
atan		sinh
cosh
tanh

うっかり $\sqrt{x^2} = x$ としないように。SymPy はデフォルトでは…

In [26]:
sqrt(x**2)
Out[26]:
$\displaystyle \sqrt{x^{2}}$

$x$ を実数としてやると…

In [27]:
x = Symbol('x', real=True)

sqrt(x**2)
Out[27]:
$\displaystyle \left|{x}\right|$
In [28]:
# 実数の設定を初期化する

x = Symbol('x')

sqrt(x**2)
Out[28]:
$\displaystyle \sqrt{x^{2}}$

ピタゴラスの定理をみたす整数の例。
$\sqrt{3^2 + 4^2} = 5$ ですね。

In [29]:
sqrt(3**2 + 4**2)
Out[29]:
$\displaystyle 5$

$e^{\log x}$ や $\log(e^2)$ の計算。

In [30]:
exp(log(x))
Out[30]:
$\displaystyle x$
In [31]:
log(E**2)
Out[31]:
$\displaystyle 2$

三角関数の値・引数の単位

三角関数の値を数値で求めたいときには，以下のようにします。

$\displaystyle \sin \frac{\pi}{3}$ の値は…

In [32]:
sin(pi/3)
Out[32]:
$\displaystyle \frac{\sqrt{3}}{2}$

float() 関数を使って，直前の結果を浮動小数点表示します。

In [33]:
float(_)
Out[33]:
0.8660254037844386

変数 Pi に浮動小数点表示の $\pi$ の値を代入します。 浮動小数点表示で数値を入れると， sin() も浮動小数点表示で答えを返します。

In [34]:
Pi = float(pi)
sin(Pi/3)
Out[34]:
$\displaystyle 0.866025403784439$

三角関数の引数はラジアンです。度を使って求めたいときは以下のようにします。

度をラジアンに変換する関数 degrad を定義します。

In [35]:
def degrad(x):
    return Rational(x, 180)*pi

$\sin 60^{\circ}$ を求める場合は degrad(60) を引数にして sin の値を求めます。

In [36]:
sin(degrad(60))
Out[36]:
$\displaystyle \frac{\sqrt{3}}{2}$

練習 1-2

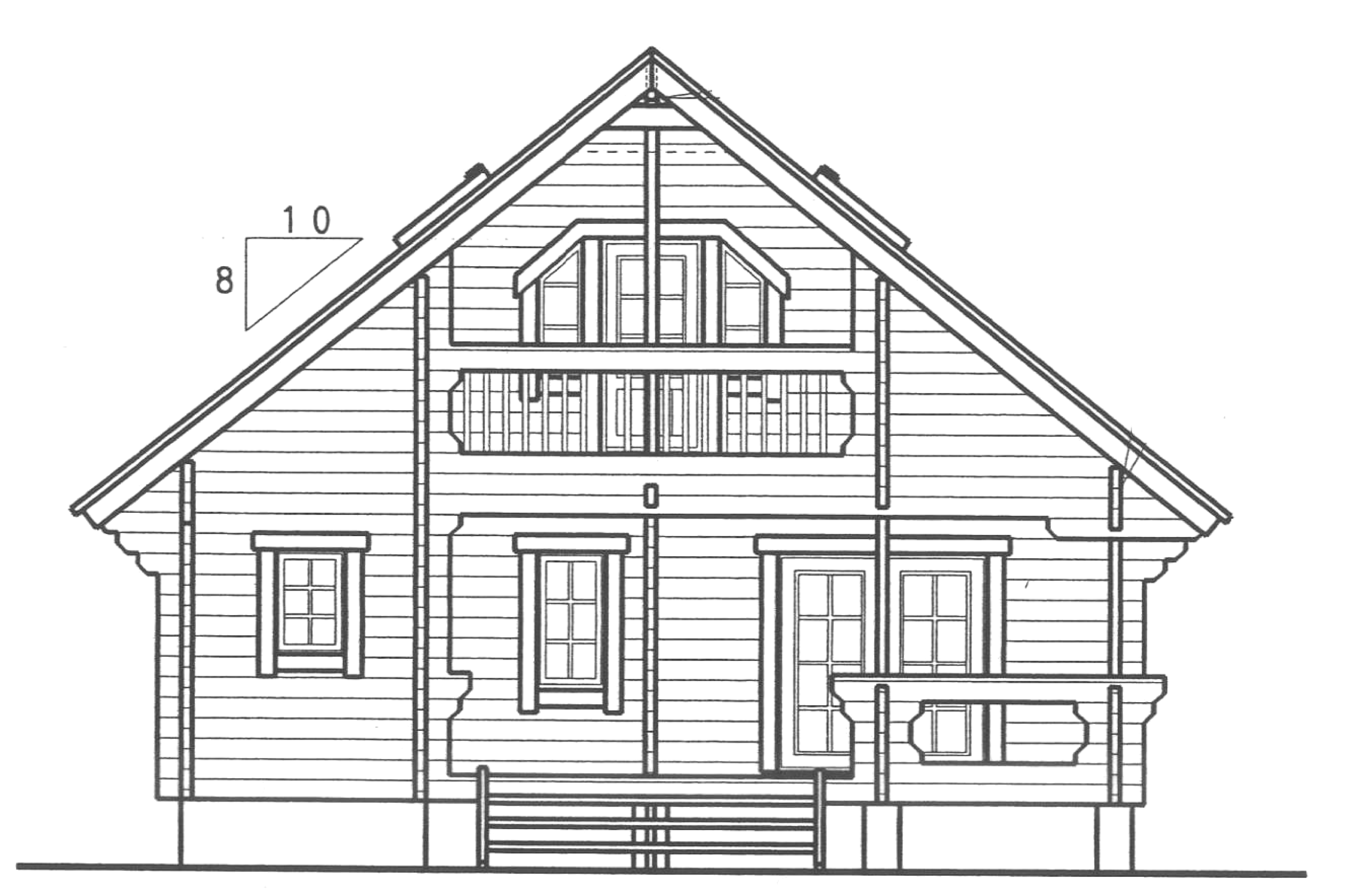
（練習）屋根勾配

家の屋根の勾配は角度ではなく，伝統的に 3 寸勾配，4 寸勾配のように水平方向に 1 尺(10 寸)に対して垂直方向に何寸立ち上がるかで示します。

図のログハウスの屋根は 8 寸勾配です。
傾斜角度にすると何度ですか?

ラジアンを度に変換する関数を作っておきます。

In [37]:
def raddeg(x):
    return float(x * 180/pi)
In [38]:
# 8寸勾配となる角度を求める

atan(0.8)
Out[38]:
$\displaystyle 0.674740942223553$
In [39]:
# 度になおす

raddeg(_)
Out[39]:
38.659808254090095

以下に各寸勾配の角度の表があります。10 寸勾配（矩勾配　かねこうばい）まで表
を完成させましょう。

勾配1寸勾配2寸勾配3寸勾配…
atan(0.1)atan(0.2)atan(0.3)…
rad0.09970.19740.2915…
度5.7106°11.3099°16.6992°…

練習 1-3

(練習)加法定理・三倍角の公式

  1. 三角関数及び双曲線関数の加法定理を確認しなさい。
  2. $\sin 3x$ を $\sin x$ だけを使って表しなさい。
  3. $\tan 3x$ を $\tan x$ だけを使って表しなさい.
In [40]:
# ヒント。
# trig=True オプションをつけて expand() で展開する。

expand(sin(x + y), trig=True)
Out[40]:
$\displaystyle \sin{\left(x \right)} \cos{\left(y \right)} + \sin{\left(y \right)} \cos{\left(x \right)}$
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:

微分・積分・数値積分

微分・積分を行う関数の表記を以下に示します。

操作表記例
微分diff(f(x), x)
n 階微分diff(f(x), x, n)
不定積分integrate(f(x), x)
定積分integrate(f(x), (x, a, b))
数値積分integrate(f(x), (x, a, b)).evalf()

微分・積分

$x^3 + 5 x + 2$ を $x$ で微分します。とっとと答えだけを表示させるには…

In [41]:
diff(x**3 + 5*x + 2, x)
Out[41]:
$\displaystyle 3 x^{2} + 5$

何を計算させるのかを表示させてから答えを表示させるには…

In [42]:
Eq(
    diff(x**3 + 5*x + 2, x, evaluate=False), 
    diff(x**3 + 5*x + 2, x)
)
Out[42]:
$\displaystyle \frac{d}{d x} \left(x^{3} + 5 x + 2\right) = 3 x^{2} + 5$

または，以下のように書いてもよいです。

In [43]:
Eq(
    Derivative(x**3 + 5*x + 2, x), 
    Derivative(x**3 + 5*x + 2, x).doit()
)
Out[43]:
$\displaystyle \frac{d}{d x} \left(x^{3} + 5 x + 2\right) = 3 x^{2} + 5$

不定積分の例：

In [44]:
Eq(
    Integral(x**2 * cos(x) + 2*x*sin(x), x), 
    integrate(x**2 * cos(x) + 2*x*sin(x), x)
)
Out[44]:
$\displaystyle \int \left(x^{2} \cos{\left(x \right)} + 2 x \sin{\left(x \right)}\right)\, dx = x^{2} \sin{\left(x \right)}$

定積分の例：

In [45]:
Eq(
    Integral(sin(x), (x, 0, pi/2)),
    Integral(sin(x), (x, 0, pi/2)).doit()
)
Out[45]:
$\displaystyle \int\limits_{0}^{\frac{\pi}{2}} \sin{\left(x \right)}\, dx = 1$

数値積分

では，解析的に積分できない場合はどうするか？

実際，大学で習う「初等関数」およびその合成関数は全て微分できますが，では初等関数およびその合成関数（初等関数を使って書かれる関数）は全て積分できるかというと，そうではない。

大学の授業，たとえば理工系の数学Bなどでは，解析的に積分できるような例題だけを扱いますが，実際には，以下の例のように $\sin(\sin x)$ などのような単純な例でも，解析的には積分できません。

解析的に積分できない場合は，数値積分によって近似値を求めます。

$\displaystyle \int_0^{\pi} \sin(\sin x)\ dx$ の計算をします。解析的に解けないとそのまま返します。

In [46]:
integrate(sin(sin(x)), (x, 0, pi))
Out[46]:
$\displaystyle \int\limits_{0}^{\pi} \sin{\left(\sin{\left(x \right)} \right)}\, dx$

以下のように .evalf() をつけると数値積分してくれます。

In [47]:
integrate(sin(sin(x)), (x, 0, pi)).evalf()
Out[47]:
$\displaystyle 1.78648748195005$

方程式

多項式方程式・連立方程式

SymPy は，式の計算だけでなく，代数方程式を解くことができます。例を以下に示します。

$x^2 + 2 x – 2 = 0$ を $x$ について解きます。

In [48]:
solve(x**2 + 2*x -2, x)
Out[48]:
[-1 + sqrt(3), -sqrt(3) - 1]

連立方程式 $x^2 + y^2 = 5, \ x + y = 1$ を $x, y$ について解きます。

In [49]:
solve([x**2 + y**2 - 5, x + y -1], [x, y])
Out[49]:
[(-1, 2), (2, -1)]

3 次方程式 $x^3 – 8 = 0$ を解きます。

In [50]:
sols = solve(x**3 - 8)
sols
Out[50]:
[2, -1 - sqrt(3)*I, -1 + sqrt(3)*I]

念のため，3番目の答え（Python はゼロからはじまることに注意）を3乗して展開すると…

In [51]:
sols[2]**3
Out[51]:
$\displaystyle \left(-1 + \sqrt{3} i\right)^{3}$
In [52]:
expand(_)
Out[52]:
$\displaystyle 8$

練習 1-4

（練習）鶴と亀と蟻

鶴と亀と蟻，個体数の合計は 10。足の数は全部で 34 本。蟻は亀より 1 匹少ない。鶴，亀，蟻，それぞれ何羽・何匹?

鶴と亀と蟻の個体数をそれぞれ $x, y, z$ として連立方程式をたてて solve します。蟻の足は何本かわかりますよね?

かつて線形代数の授業でこの問題を出したとき，真っ先に出た質問が「先生，蟻の足は何本ですか？」でした… orz

方程式の数値解

多項式方程式でない場合は，nsolve() 関数を使って数値解を探します。

関数 $g(x):= (x − 1)\,e^x$ の定義。

In [53]:
def g(x):
    return (x - 1)*exp(x)

$g(x) – 1 = 0$ の解は，一般には solve() で求めることができません。（が，以下の例では Lambert W 関数を使って解いてしまっています… ）

In [54]:
solve(g(x) - 1)
Out[54]:
[LambertW(exp(-1)) + 1]

nsolve() 関数を使って，$x=1$ のあたりからはじめて16桁の精度で数値解を求める例。nsolve() を使う際には，最初どのへんの $x$ から始めるかを指定する必要があります。

In [55]:
nsolve(g(x) - 1, x, 1, prec=16)
Out[55]:
$\displaystyle 1.278464542761074$

出た数値解を $g(x)$ に代入して値を確かめると…

In [56]:
g(_)
Out[56]:
$\displaystyle 1.0$

$g(x)$ がどのへんで $1$ になるかは，以下のようにグラフを描いてみればわかります。Python でのグラフ作成については，別途解説します。

In [57]:
# SymPy Plotting Backends (SPB) を使ってみる
from spb import *

# グラフを SVG で Notebook にインライン表示
%config InlineBackend.figure_formats = ['svg']
In [58]:
plot(g(x)-1, (x, 0, 5), ylim = (-1, 1), ylabel = "$g(x)-1$");

練習 1-5

（練習）関数の極大値

次の関数が極大値をとる $x$ の値およびその極大値を求めよ。

$$ 1. \ \ f(x) = \frac{x^3}{e^x – 1}, \qquad 2. \ \ g(x) = \frac{x^5}{e^x -1}$$

In [59]:
# 1. のヒント

def f(x):
    return x**3/(exp(x)-1)

# f(x) の導関数の定義。
def df(x1):
    return diff(f(x),x).subs(x, x1)

# 導関数 df(x) のグラフを描き，ゼロとなる x のあたりをつける
plot(df(x), (x, 0.1, 10), ylabel="$df(x)$");

In [60]:
# 上のグラフから，2 < x < 4 で df(x) = 0 となることがわかったので
# x = 3 のあたりで df(x) = 0 となる x を nsolve() で求める。

nsolve(df(x), x, 2, prec=16)
Out[60]:
$\displaystyle 2.821439372122079$
In [61]:
# 極値をとるときの x の値はわかったので，
# そのときの f(x) の極大値は

f(_)
Out[61]:
$\displaystyle 1.421435472747737$
In [62]:
# 2. の問題も同様に

参考：プランクの法則

熱力学，気象学，天文学，宇宙物理学等で現れる「プランクの法則」。

温度 $T$ の黒体から放射される電磁波の放射強度は周波数を $\nu$ として以下のように与えられる。

$$I(\nu, T) = \frac{2h\nu^3}{c^2} \frac{1}{e^{h\nu/kT} – 1}$$

ここで，$\displaystyle x \equiv \frac{h\nu}{kT}$ とおくと

$$I(\nu, T) = \frac{2 (k T)^3}{h^2 c^2} \frac{x^3}{e^{x} – 1} \equiv C \frac{x^3}{e^{x} – 1}$$

となり，$f(x)$ の極大値を調べることは，プランクの法則で与えられる黒体からの放射強度の極大値を調べることにつながるんですよ。