Maxima の2次元グラフ作成は plot2d() でもできますが，ここでは，draw2d() について説明します。

Maxima を使って，関数のグラフを描くことができます。また，数値データもグラフにすることができます。

Maxima の2次元グラフ作成は plot2d() でもできますが，ここでは，draw2d() について説明します。
draw2d() でプロットできるオブジェクトは以下のとおりです。

陽関数 $y = f(x)$:
- explicit(f(x), x, xmin, xmax)
陰関数 $f(x, y) = 0$:
- implicit(f(x, y) = 0, x, xmin, xmax, y, ymin, ymax)
媒介変数表示 $x(t), y(t)$:
- parametric(x(t), y(t), t, tmin, tmax)
点，$x$ 座標 $y$ 座標の数値データ:
- points([[x1, y1], [x2, y2], ... ])
  または points([x1, x2, ... ], [y1, y2, ...])
ベクトル，始点 $x_0, y_0$ からベクトル成分 $v_x, v_y$:
- vector([x0, y0], [vx, vy])

また，2本の陽関数で挟まれた領域を塗りつぶすこともできます。

陽関数のグラフ

例として，$y = \sin x$ のグラフを $−2\pi \leq x \leq 2\pi$ の範囲で描きます。基本的な定数の一つである円周率 $\pi$ は Maxima では %pi と書くのでしたね。

In [1]:

draw2d(
  explicit(sin(x), x, -2*%pi, 2*%pi)
)$

In [2]:

/* オプションの設定例 */
draw2d(
  /* フォント設定 */
  font = "Arial", 
  font_size = 16, 
  /* 表示範囲 */
  xrange = [-10, 10], yrange = [-1.1, 1.1],
  /* x 軸 y 軸の表示 */
  xaxis = true, yaxis = true, 
  /* グリッド */
  grid=true,

  /* 凡例 */
  key = "正弦関数", 
  /* 色 */
  color = red, 
  /* 線の太さ */
  line_width = 2,
  explicit(sin(x), x, -2*%pi, 2*%pi)
)$

陰関数のグラフ

例として，$x^2 + y^2 = 1$ のグラフを描きます。$y$ について解いて陽関数の形にしたり，以下で述べるような媒介変数表示にしなくても，陰関数のまま，グラフに描くことができます。

In [3]:

draw2d(
  implicit(x**2 + y**2 = 1, x, -1.2, 1.2, y, -1.2, 1.2)
)$

In [4]:

/* オプションの設定例 */
draw2d(
  /* 滑らかにするためにサンプリンググリッドを多めに */
  ip_grid = [200, 200], 
  /* 縦横比 */
  proportional_axes = xy,
  /* x 軸 y 軸の表示 */
  xaxis = true, yaxis = true, 
  
  implicit(x**2 + y**2 = 1, x, -1.5, 1.5, y, -1.5, 1.5)
)$

媒介変数表示のグラフ

半径 $1$ の円の方程式は $x^2 +y^2 = 1$ です。この円を以下のような媒介変数表示にして描きます。

$$ x=\cos t, \quad y=\sin t \quad (0 \leq t \leq 2\pi) $$

In [5]:

draw2d(
  parametric(cos(t), sin(t), t, 0, 2*%pi)
)$

In [6]:

/* オプションの設定例 */
draw2d(
  /* 滑らかにするためにサンプリングを多めに */
  nticks = 100, 
  /* 縦横比。*/
  proportional_axes = xy,
  /* 表示範囲 */
  xrange = [-1.1, 1.1], yrange = [-1.1, 1.1],
  /* x 軸 y 軸の表示 */
  xaxis = true, yaxis = true, 
  
  parametric(cos(t), sin(t), t, 0, 2*%pi)
)$

点・数値データのグラフ

以下の例では，最初（左側）の数値を $x$ 座標の値，次（右側）の数値を $y$ 座標の値として 6 個の点からなるリスト data の各点をつないだ折れ線グラフを描きます。

In [7]:

data: makelist([i, i^2], i, 0, 5);

Out[7]:

\[\tag{${\it \%o}_{7}$}\left[ \left[ 0 , 0 \right] , \left[ 1 , 1 \right] , \left[ 2 , 4 \right] , \left[ 3 , 9 \right] , \left[ 4 , 16 \right] , \left[ 5 , 25 \right] \right] \]

In [8]:

draw2d(
  points(data)
)$

In [9]:

/* オプションの設定例 */
draw2d(
  /* 表示範囲 */
  xrange = [0, 5], yrange = [0, 28],

  /* 点を塗りつぶした丸に */
  point_type = 7,
  /* 点の大きさ */
  point_size = 1,
  /* 色 */
  color = purple,
  points(data)
)$

point_type には以下の種類があります。

none (-1)
dot (0)
plus (1)
multiply (2)
asterisk (3)
square (4) 
filled_square (5)
circle (6)
filled_circle (7)
up_triangle (8)
filled_up_triangle (9)
down_triangle (10) 
filled_down_triangle (11)
diamant (12)
filled_diamant (13)

ベクトルを描く

原点を始点とし，$v_x = 0.5, v_y = 1$ のベクトルを描きます。

In [10]:

/* オプションを指定しないと変なベクトルに... */
draw2d(
  vector([0, 0], [0.5, 1])
)$

In [11]:

/* オプションの設定例 */
draw2d(
  /* 表示範囲 */
  xrange = [-1.5, 1.5], yrange = [-1.5, 1.5],
  /* 縦横比。*/
  proportional_axes = xy,
  /* x 軸 y 軸の表示 */
  xaxis = true, yaxis = true, 

  /* ベクトルの矢の設定 */
  head_length = 0.1,
  head_angle  = 20, 

  vector([0, 0], [0.5, 1])
)$

複数のベクトルやベクトル場などを描く例。

In [12]:

x(t):= 2 * t$
y(t):= 2 * t - t**2$

vx(t):= 2$
vy(t):= 2 - 2*t$

scaling: 0.2$
vecV: 
  makelist(
    vector(1.0*[x(t/2), y(t/2)], scaling*[vx(t/2), vy(t/2)]), t, 0, 4)$

for v in vecV do(print(v))$
/* 以下のように vecV は 5本のベクトルのリストになっている */

${\it vector}\left(\left[ 0 , 0 \right] , \left[ 0.4 , 0.4 \right] \right)$

${\it vector}\left(\left[ 1.0 , 0.75 \right] , \left[ 0.4 , 0.2 \right] \right)$

${\it vector}\left(\left[ 2.0 , 1.0 \right] , \left[ 0.4 , 0 \right] \right)$

${\it vector}\left(\left[ 3.0 , 0.75 \right] , \left[ 0.4 , -0.2 \right] \right)$

${\it vector}\left(\left[ 4.0 , 0 \right] , \left[ 0.4 , -0.4 \right] \right)$

In [13]:

draw2d(
  /* 表示範囲 */
  xrange = [-0.5, 4.5], yrange = [-0.5, 2],
  /* 縦横比 */
  proportional_axes=xy,
  /* グリッド。y 軸の目盛を 1 ごとに */
  grid = true,
  ytics = 1, 
  xaxis = true, yaxis = true,
  /* ベクトルの矢の設定 */
  head_length = 0.1,
  head_angle  = 20, 
  
  vecV
)$

さらには以下のようなベクトル場のグラフも描くことができます。参考までに。

参考：Maxima でベクトル場（電場・磁場）を描く

複数のグラフを重ねて表示

複数のグラフを重ねて表示する例を示します。

$y = x^2 – 1$ と $y = 4 x – 5$ の 2つの陽関数のグラフを重ねて描きます。

In [14]:

draw2d(
  explicit(x**2 - 1, x, -5, 5),
  explicit(4*x - 5, x, -5, 5)
)$

plot2d() の場合と違い，自動で色を変えてはくれません。いくつかオプションを設定して描く例です。それぞれの関数を explicit() で描く直前に，それぞれのオプションを指定します。

In [15]:

/* オプションの設定例 */
draw2d(
  /* フォント設定 */
  font = "Arial", 
  font_size = 16,
  /* 表示範囲 */
  xrange = [-5, 5], yrange = [-5, 10],
  /* x 軸 y 軸の表示 */
  xaxis = true, yaxis = true, 
  /* 凡例の位置 */
  user_preamble = "set key bottom",

  color = red,
  line_width = 4,
  key = "x^2 - 1",
  explicit(x**2 - 1, x, -5, 5),
  
  color = black,
  line_width = 1,
  key = "4 x - 5",
  explicit(4*x - 5, x, 1, 3)
  /* x の範囲も別個に設定可能 */
)$

上のグラフをみると，2 つのグラフは 1 点で接しているように見えます。

実際に $y = 4x – 5$ が接線であることを示してみましょう。

$x^2 – 1 = 4 x – 5$ の解が1つであることを示せば十分ですね。

In [16]:

sol: solve(x^2 - 1 = 4*x - 5, x);

Out[16]:

\[\tag{${\it \%o}_{22}$}\left[ x=2 \right] \]

$y = f(x)$ の $x = x_1$ における接線の方程式は，
$$ y – f(x_1) = f'(x_1) \,(x – x_1)$$ ですから，$x = x_1$ における接線の方程式をあからさまに書くと…

In [17]:

f(x):= x^2 - 1;
define(df(x), diff(f(x), x));

x1: rhs(sol[1]);
y = df(x1) * (x - x1) + f(x1), ratsimp;

Out[17]:

\[\tag{${\it \%o}_{23}$}f\left(x\right):=x^2-1\]

Out[17]:

\[\tag{${\it \%o}_{24}$}{\it df}\left(x\right):=2\,x\]

Out[17]:

\[\tag{${\it \%o}_{25}$}2\]

Out[17]:

\[\tag{${\it \%o}_{26}$}y=4\,x-5\]

練習 4-1

$y = f(x) = x^2 -1$ の $x = 1$ における接線，および $ x = 3$ における接線の方程式を求め，これら3本の線および接点をグラフに描け。

In [18]:

f(x):= x^2 - 1;
define(df(x), diff(f(x), x));

Out[18]:

\[\tag{${\it \%o}_{27}$}f\left(x\right):=x^2-1\]

Out[18]:

\[\tag{${\it \%o}_{28}$}{\it df}\left(x\right):=2\,x\]

$y = f(x)$ の $x = x_1$ における接線の方程式は，
$$ y – f(x_1) = f'(x_1) \,(x – x_1)$$ ですから…

In [ ]:

数値データファイルを読み込む

Maxima では，あらかじめ作成された数値データファイルを読み込んでグラフを描くこともできます。

以下のような内容のファイル test.dat がカレントディレクトリにあるとします。（ない場合は，弘大 JupyterHub の Home で「新規」から「テキストファイル」を選択し，以下の数値をコピペし，「test.dat」にリネームし，保存してください。）

データファイルを読み込む Maxima の関数は，read_nested_list を使います。

In [19]:

dat: read_nested_list("test.dat");

Out[19]:

\[\tag{${\it \%o}_{29}$}\left[ \left[ 0 , 0 \right] , \left[ 1 , 1 \right] , \left[ 2 , 4 \right] , \left[ 3 , 9 \right] , \left[ 4 , 16 \right] , \left[ 5 , 25 \right] \right] \]

リスト dat に読み込んだ数値データを plot2d() でグラフにします。

In [20]:

draw2d(
  points(dat)
)$

In [21]:

/* オプションの設定例 */
draw2d(
  user_preamble = "set key top left", 
  
  point_type = 7, 
  point_size = 1,
  color = red, 
  key = "データ",
  points(dat)
)$

数値データと理論曲線を重ねて表示

前節の数値データファイル test.dat と理論曲線 $y = x^2$ の 2 つのグラフを重ねて表示してみます。

In [22]:

draw2d(
  user_preamble = "set key top left",
 
  /* 数値データを点で */
  point_type = 7, 
  point_size = 1,
  color = 1, 
  key = "データ",
  points(dat), 

  /* 曲線を陽関数で */
  color = 2,
  key = "理論曲線 y = x^2", 
  explicit(x**2, x, 0, 5)
)$

練習 4-2

楕円のグラフ（楕円中心を原点にして）

媒介変数表示のグラフを複数重ねて表示する例です。

原点を中心とし，長半径 $a$，単半径 $b$ の楕円の式は

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$

媒介変数表示では，$x=a \cos t, \ y=b \sin t, \ (0\leq t\leq 2\pi)$と書けます。
$a$，$b$ に適当な値を入れて複数の楕円のグラフを重ねて描きなさい。

In [23]:

/* ヒント：媒介変数 t 表示の x, y を関数として定義 */
x(a, t):= a*cos(t)$
y(b, t):= b*sin(t)$

In [ ]:

海王星と冥王星の軌道

焦点を原点とした楕円のグラフ

太陽からの万有引力を受けて運動する惑星は，太陽（二体問題では質量中心）を焦点の一つとした楕円運動を描いて運動します。
焦点の一つを原点とし，長半径 $a$，離心率 $e$ の楕円の方程式は，極座標 $r$，$\varphi$ を使って以下のように表すことができます。

$$ r= \frac{a (1−e^2)}{ 1 + e\cos\varphi}$$

さて，かつては第9惑星，現在では準惑星の一つである冥王星も楕円軌道を描きます。冥王星の軌道長半径 $𝑎_P=39.445 \mbox{au}$，離心率 $𝑒_P=0.250$
を使って冥王星の軌道を描きます。

参考：冥王星 – Wikipedia

まず，極座標表示の楕円の式を関数として定義します。

In [24]:

r(a, e, phi):= a*(1-e^2)/(1+e*cos(phi));
x(a, e, phi):= r(a, e, phi)*cos(phi);
y(a, e, phi):= r(a, e, phi)*sin(phi);

Out[24]:

\[\tag{${\it \%o}_{35}$}r\left(a , e , \varphi\right):=\frac{a\,\left(1-e^2\right)}{1+e\,\cos \varphi}\]

Out[24]:

\[\tag{${\it \%o}_{36}$}x\left(a , e , \varphi\right):=r\left(a , e , \varphi\right)\,\cos \varphi\]

Out[24]:

\[\tag{${\it \%o}_{37}$}y\left(a , e , \varphi\right):=r\left(a , e , \varphi\right)\,\sin \varphi\]

冥王星の軌道長半径と離心率：

In [25]:

aP: 39.445$
eP: 0.250$

In [26]:

draw2d(
  /* 滑らかにするためにサンプリングを多めに */
  nticks = 200, 
  /* 縦横比。*/
  proportional_axes = xy,
  /* 表示範囲 */
  xrange = [-50, 50], yrange = [-50, 50],
  /* x 軸 y 軸の表示 */
  xaxis = true, yaxis = true, 

  key = "冥王星",
  parametric(x(aP, eP, phi), y(aP, eP, phi), phi, 0, 2*%pi)
)$

では，この冥王星の軌道と，その内側をまわる海王星の軌道を重ねて描いてみましょう。

海王星の軌道長半径は $a_N=30.181 \mbox{au}$，離心率は $e_N=0.0097$ と小さいので簡単のために $e_N=0$ として扱います。

参考：海王星 – Wikipedia

実際の2つの天体の軌道は同じ平面上にありませんが，太陽からの距離のみをみるために，ここでは同一平面上に描きます。

In [27]:

aN: 30.181$
eN: 0$

In [28]:

draw2d(
  /* 滑らかにするためにサンプリングを多めに */
  nticks = 200, 
  /* 縦横比。*/
  proportional_axes = xy,
  /* 表示範囲 */
  xrange = [-50, 50], yrange = [-50, 50],
  /* x 軸 y 軸の表示 */
  xaxis = true, yaxis = true, 

  key = "冥王星",
  color = blue,
  parametric(x(aP, eP, phi), y(aP, eP, phi), phi, 0, 2*%pi), 
  
  key = "海王星",
  color = red,
  parametric(x(aN, eN, phi), y(aN, eN, phi), phi, 0, 2*%pi)
)$

さて，この冥王星と海王星の軌道のグラフをいると，軌道が交差しているように見えます。このことを確かめます。

表示される領域を制限して，交差しているあたりを拡大してみます。

In [29]:

draw2d(
  nticks = 200, 
  proportional_axes = xy,

  /* 表示範囲を適宜調整すること */
  xrange = [20, 30], yrange = [10, 20],

  xaxis = true, yaxis = true, 

  key = "冥王星",
  parametric(x(aP, eP, phi), y(aP, eP, phi), phi, 0, 2*%pi), 
  
  key = "海王星",
  color = red,
  parametric(x(aN, eN, phi), y(aN, eN, phi), phi, 0, 2*%pi)
)$

海王星の軌道は半径 $a_N$ の円としていますから，以下の式を満たす角度 $\varphi$
を求めればよいことになります。

$$ r(a_P, e_P, \varphi) = a_N$$

$0 < \varphi < \pi/2$
のどこかで交差しているようですから，このあたりで数値的に解を求める方法は以下の通りです。

In [30]:

phi1: find_root(r(aP, eP, t) = aN, t, 0, %pi/2);

Out[30]:

\[\tag{${\it \%o}_{45}$}0.4485997043415258\]

$ -\pi/2 < \varphi < 0$ の範囲でも交差していますね。
対称性から答えは phi1 に負号をつけたものになるのは明らかですが，念のために確かめます。

In [31]:

phi2: find_root(r(aP, eP, t) = aN, t, -%pi/2, 0);

Out[31]:

\[\tag{${\it \%o}_{46}$}-0.4485997043415258\]

求めた角度はラジアン単位ですから，度に直してみます。

In [32]:

/* 今後表示するケタ数を 4 に */ 
fpprintprec: 4$ 

float(phi1*180/%pi);
% * 2;

Out[32]:

\[\tag{${\it \%o}_{48}$}25.7\]

Out[32]:

\[\tag{${\it \%o}_{49}$}51.41\]

つまり一周 360 度のうち，この角度にあたる分は，海王星のほうが冥王星より太陽から遠い位置にあることがわかります。

原点と 2 つの軌道の交点を結ぶ直線を描く方法は以下の通りです。

In [33]:

draw2d(
  /* 滑らかにするためにサンプリングを多めに */
  nticks = 200, 
  /* 縦横比。*/
  proportional_axes = xy,
  /* 表示範囲 */
  xrange = [-50, 50], yrange = [-50, 50],
  /* x 軸 y 軸の表示 */
  xaxis = true, yaxis = true, 

  /* 点と点を線でつなぐ */
  points_joined = true, 
  /* 端点には●などをつけない */
  point_type = none,
  color = black,
  points([[0, 0], [aN*cos(phi1), aN*sin(phi1)]]),
  points([[0, 0], [aN*cos(phi2), aN*sin(phi2)]])
)$

練習 4-3

原点と2つの軌道の交点を結ぶ直線を追加して，冥王星と海王星の軌道を描け。

In [ ]:

月別平年気温の関数フィット

弘前市の月別平年気温のデータを使ってリスト HiroT を作ります。

参考：弘前　平年値（年・月ごとの値）　主な要素

In [34]:

HiroT: [
[1, -1.5],
[2, -1.0],
[3, 2.3],
[4, 8.6],
[5, 14.3],
[6, 18.3],
[7, 22.3],
[8, 23.5],
[9, 19.4],
[10, 12.9],
[11, 6.5],
[12, 0.8]
];

Out[34]:

\[\tag{${\it \%o}_{51}$}\left[ \left[ 1 , -1.5 \right] , \left[ 2 , -1.0 \right] , \left[ 3 , 2.3 \right] , \left[ 4 , 8.6 \right] , \left[ 5 , 14.3 \right] , \left[ 6 , 18.3 \right] , \left[ 7 , 22.3 \right] , \left[ 8 , 23.5 \right] , \left[ 9 , 19.4 \right] , \left[ 10 , 12.9 \right] , \left[ 11 , 6.5 \right] , \left[ 12 , 0.8 \right] \right] \]

このデータをグラフに描いてみます。

In [35]:

draw2d(
  point_type = 7,  
  points(HiroT)
)$

グラフを見ると，月別平年気温は 12 ヶ月周期の三角関数でフィットできるようにみえます。

では，以下のように関数フィットをしてみましょう。

まず，最小二乗法のパッケージ lsquares をロードします.これは lsquares_estimates を初めて使う際，最初に 1 回だけ行えばよいです。

In [36]:

load(lsquares)$

次に，以下のような関数を定義して，うまくフィットするように定数 a0, a1, b1, a2, b2 を求めます。

In [37]:

g(x):= a0/2 + a1*cos(2*%pi*x/12) + b1*sin(2*%pi*x/12) 
            + a2*cos(4*%pi*x/12) + b2*sin(4*%pi*x/12);

Out[37]:

\[\tag{${\it \%o}_{54}$}g\left(x\right):=\frac{a_{0}}{2}+a_{1}\,\cos \left(\frac{2\,\pi\,x}{12}\right)+b_{1}\,\sin \left(\frac{2\,\pi\,x}{12}\right)+a_{2}\,\cos \left(\frac{4\,\pi\,x}{12}\right)+b_{2}\,\sin \left(\frac{4\,\pi\,x}{12}\right)\]

参考：フーリエ級数展開

一般に周期 $2L$ の周期関数は，以下のようにフーリエ級数展開できるのであった。したがって，ここでやっていることは，12ヶ月分の月平年気温という数値データに対して，フーリエ級数展開みたいなことを数値的に行っていると考えることができる。

$$ f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty} \bigl( a_n \cos \left(n \frac{\pi}{L} {x}\right) + b_n \sin \left(n\frac{\pi}{L} {x}\right) \bigr) $$

最小二乗法を行う関数 lsquares_estimates には数値データを行列として入れてやる必要があります。

このためにリスト HiroT を行列 M に変換します。（リストと行列では表示が異なります。行列は行列らしく表示されています。）

In [38]:

/* リスト HiroT を行列 M に変換する */
M: apply('matrix, HiroT);

Out[38]:

\[\tag{${\it \%o}_{55}$}\begin{pmatrix}1 & -1.5 \\ 2 & -1.0 \\ 3 & 2.3 \\ 4 & 8.6 \\ 5 & 14.3 \\ 6 & 18.3 \\ 7 & 22.3 \\ 8 & 23.5 \\ 9 & 19.4 \\ 10 & 12.9 \\ 11 & 6.5 \\ 12 & 0.8 \\ \end{pmatrix}\]

In [39]:

/* 最小二乗法で a0, a1, ... を求める */
lsquares_estimates(M, [x, y], y=g(x), [a0, a1, b1, a2, b2])$
/* 直前の答え a0, a1, ... を不動小数点表示する */
float(%);

Out[39]:

\[\tag{${\it \%o}_{57}$}\left[ \left[ a_{0}=21.07 , a_{1}=-9.161 , b_{1}=-8.34 , a_{2}=-0.6333 , b_{2}=0.1443 \right] \right] \]

最小二乗法によって求めた a0, a1, b1, a2, b2 の値を gfit に代入し，この関数のグラフを描きます。

In [40]:

gfit: ev(g(x), %);

Out[40]:

\[\tag{${\it \%o}_{58}$}0.1443\,\sin \left(\frac{\pi\,x}{3}\right)-0.6333\,\cos \left(\frac{\pi\,x}{3}\right)-8.34\,\sin \left(\frac{\pi\,x}{6}\right)-9.161\,\cos \left(\frac{\pi\,x}{6}\right)+10.53\]

In [41]:

draw2d(
  xrange = [0.5, 12.5], yrange = [-5, 28],
  xaxis = true, yaxis = true, 
  user_preamble = "set xtics 1", 
  xlabel = "月", 
  ylabel = "月別平年気温",
  title = "弘前市の月別平年気温",
  
  explicit(gfit, x, 1, 12)
)$

練習 4-4

月別平年気温の数値データとフィット曲線のグラフを重ねて描け。

In [ ]:

領域の塗りつぶし

$y = f(x)$ と $y = g(x)$ （$f(x) \geq g(x)$）で囲まれた領域を塗りつぶす例。

In [42]:

f(x):= 0.6*x + 0.4*cos(x)$
g(x):= 0$

draw2d(
  xrange = [-0, 2.5], yrange = [-0.2,1.5],
  xaxis = true,
  /* 塗りつぶす色の指定。*/
  fill_color = yellow, 
  
  /* 上の線。*/
  filled_func = f(x), 
  
  /* 下の線と範囲の指定。*/
  explicit(g(x), x, 0.5, 2), 
  
  /* 塗り潰し終了 */
  filled_func = false, 
  
  /* あらためて y = f(x) を描く */
  color = blue, 
  line_width = 2, 
  explicit(f(x), x, 0.25, 2.25)
)$

練習 4-5

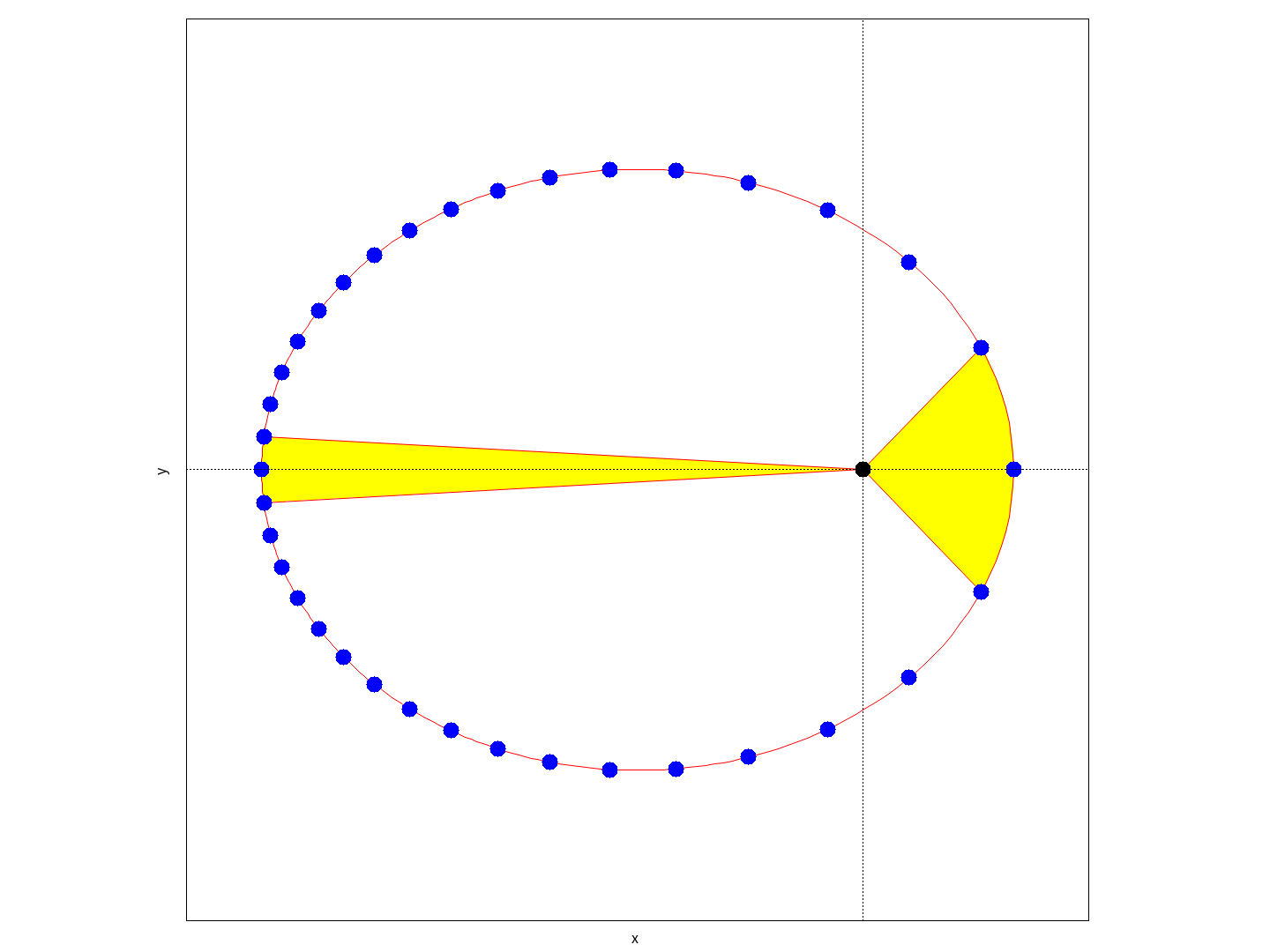
半径 $1$ の円において，以下の扇形の領域を塗りつぶす。

中心から $\theta = -15^{\circ}$ と $\theta = 15^{\circ}$ の直線で囲まれた領域
中心から $\theta = 100^{\circ}$ と $\theta = 130^{\circ}$ の直線で囲まれた領域

円のグラフの描き方にはいろいろありますが，今回は塗りつぶしなので，陽関数で表現する必要があります。

\begin{eqnarray}
x^2 + y^2 &=& 1 \\
y &=& \pm \sqrt{1 – x^2}
\end{eqnarray}

また，原点（円の中心）と円上の点 $(\cos\theta, \sin\theta)$ を結ぶ直線の方程式は

$$y = \tan\theta \cdot x$$

この問題では角度を度であらわしているので，ラジアンに換算する必要があります。

In [43]:

/* 円の方程式：上半分 */
yu(x):= sqrt(1 - x**2);
/* 円の方程式：下半分 */
yd(x):= -sqrt(1 - x**2);

/* 中心と円上の点を結ぶ直線の方程式。theta は度で */
yl(x, theta):= tan(theta*%pi/180) * x;

Out[43]:

\[\tag{${\it \%o}_{63}$}{\it yu}\left(x\right):=\sqrt{1-x^2}\]

Out[43]:

\[\tag{${\it \%o}_{64}$}{\it yd}\left(x\right):=-\sqrt{1-x^2}\]

Out[43]:

\[\tag{${\it \%o}_{65}$}{\it yl}\left(x , \vartheta\right):=\tan \left(\frac{\vartheta\,\pi}{180}\right)\,x\]

In [44]:

/* 円と theta = 15°, 15° の直線 */
draw2d(
  /* 縦横比。*/
  proportional_axes = xy,
  /* x 軸 y 軸の表示 */
  xaxis = true, yaxis = true, 

  /* 円 */
  explicit(yu(x), x, -1, 1),
  explicit(yd(x), x, -1, 1), 
  
  /* 原点からの直線 */
  explicit(yl(x, 15), x, 0, cos(15*%pi/180)),
  explicit(yl(x, -15), x, 0, cos(-15*%pi/180))
)$

In [45]:

/* 塗りつぶし 1 */
draw2d(
  /* 座標軸が塗りつぶされないように */
  user_preamble = "set grid front; unset grid;",
  
  /* 縦横比。*/
  proportional_axes = xy,
  /* x 軸 y 軸の表示 */
  xaxis = true, yaxis = true, 
  
  /* 塗りつぶす色の指定。*/
  fill_color = yellow, 
  
  /* 上の線。*/
  filled_func = yl(x, 15), 
  
  /* 下の線と範囲の指定。*/
  explicit(yl(x, -15), x, 0, cos(15*%pi/180)), 
  
  /* 塗り潰し終了 */
  filled_func = false, 

  /* 円 */
  explicit(yu(x), x, -1, 1),
  explicit(yd(x), x, -1, 1), 
  
  /* 原点からの直線 */
  explicit(yl(x, 15), x, 0, cos(15*%pi/180)),
  explicit(yl(x, -15), x, 0, cos(-15*%pi/180))
)$

In [46]:

/* 塗りつぶし 2 */
draw2d(
  /* 座標軸が塗りつぶされないように */
  user_preamble = "set grid front; unset grid;",
  
  /* 縦横比。*/
  proportional_axes = xy,
  /* x 軸 y 軸の表示 */
  xaxis = true, yaxis = true, 
  
  /* 塗りつぶす色の指定。*/
  fill_color = yellow, 
  
  /* 上の線。*/
  filled_func = yl(x, 15), 
  
  /* 下の線と範囲の指定。*/
  explicit(yl(x, -15), x, 0, cos(15*%pi/180)), 

  /* 塗り残した部分 */
  /* 上の線。*/
  filled_func = yu(x), 
  
  /* 下の線と範囲の指定。*/
  explicit(yd(x), x, cos(15*%pi/180), 1), 

  /* 塗り潰し終了 */
  filled_func = false, 

  /* 円 */
  explicit(yu(x), x, -1, 1),
  explicit(yd(x), x, -1, 1), 
  
  /* 原点からの直線 */
  explicit(yl(x, 15), x, 0, cos(15*%pi/180)),
  explicit(yl(x, -15), x, 0, cos(-15*%pi/180))
)$

In [47]:

/* 円と theta = 100°, 130° の直線 */
draw2d(
  /* 縦横比。*/
  proportional_axes = xy,
  /* x 軸 y 軸の表示 */
  xaxis = true, yaxis = true, 

  /* 円 */
  explicit(yu(x), x, -1, 1),
  explicit(yd(x), x, -1, 1), 
  
  /* 原点からの直線 */
  explicit(yl(x, 100), x, cos(100*%pi/180), 0),
  explicit(yl(x, 130), x, cos(130*%pi/180), 0)
)$

参考：

この練習問題では円ですが，天文学におけるケプラーの法則から，天体の軌道は楕円であり，面積速度が一定です。扇形の部分を塗りつぶすということは，ケプラーの第2法則を視覚的に表す際にとても重要なんですよ。

kep2

参考：Maxima でケプラー方程式を逐次近似的に解いて draw2d で描いてパラパラアニメにする

Maxima でグラフ作成 draw2d 編

陽関数のグラフ

陰関数のグラフ

媒介変数表示のグラフ

点・数値データのグラフ

ベクトルを描く

複数のグラフを重ねて表示

練習 4-1

数値データファイルを読み込む

数値データと理論曲線を重ねて表示

練習 4-2

海王星と冥王星の軌道

焦点を原点とした楕円のグラフ

練習 4-3

月別平年気温の関数フィット

参考：フーリエ級数展開

練習 4-4

領域の塗りつぶし

練習 4-5

このページの目次

このセクションの構成