Python の SciPy を使って，単振り子の運動方程式を数値的に解く。運動方程式の導出については，以下のページにまとめている。
なお，ほぼ同じ内容でグラフのみ plt.*** のみで描いた旧版のページは以下：
このページでは，（ちょっとだけ面倒だけど）以下のページに従い，ax.*** を使ってグラフを作成する。
一様重力場中の単振り子
単振り子のひもの長さを $\ell$，重力加速度の大きさを $g$，鉛直下向きからの振れ角を $\theta$ とすると，単振り子の運動方程式は
$$\frac{d^2\theta}{dt^2} = -\frac{g}{\ell} \sin\theta$$
となる。導出については，以下を参照。
振れ角が小さい場合には単振動となること
$|\theta| \ll 1$ の場合には，$\sin\theta \simeq \theta$ と近似することで，運動方程式は
$$\frac{d^2\theta}{dt^2} = -\frac{g}{\ell} \theta$$
となり，これは単振動となる。単振動の周期 $\tau_0$ は
$$\tau_0 = 2 \pi \sqrt{\frac{\ell}{g}}$$
となり，単振り子のひもの長さと重力加速度だけで決まり，初期条件で与えられる振れ角 $\theta_0$ に依存しない。これを「振り子の等時性」と言ったりする。
無次元化
単振動の周期 $\tau_0$ で無次元化した時間 $T$ を
$$T \equiv \frac{t}{\tau_0}$$
と定義する。この無次元化された時間座標で書いた運動方程式は
$$\frac{d^2 \theta}{dT^2} = -4 \pi^2 \sin\theta$$
となる。
振れ角が大きい場合の単振り子の運動
振れ角が大きい，つまり $\sin\theta \simeq \theta$ と近似できない場合は，振り子の周期は一般に振れ角に依存するのではないかと考えられる。
そこで，$T = 0$ での振れ角 $\theta_0$ をたとえば 10° から 90° まで 10° きざみで大きくしていった場合，ふりこの周期はどうなるか？ というのが問題。
運動方程式の右辺が $\sin\theta$ のままでは解析的に解けないので，以下では数値的に常微分方程式を解いて単振り子の振幅（振れ角）と周期の関係を調べる。
常微分方程式の数値解法：solve_ivp
2階常微分方程式を数値的に解くためには，連立1階微分方程式系になおす。
\begin{eqnarray}
\frac{d\theta}{dT} &=& F_1(V) = V \\
\frac{dV}{dT} &=& F_2(\theta) = -4 \pi^2 \sin\theta
\end{eqnarray}
これを初期条件 $T = 0$ で
\begin{eqnarray}
\theta(0) &=& \theta_0 \\
V(0) &=& 0
\end{eqnarray}
とし，$\theta_0 = 10^{\circ}, \ 60^{\circ}, \ 80^{\circ}$ の場合に $T_0 = 0$ から $ T_1 = 2$ まで解く。
（くどいようですが，規格化された時間で $T_1 = 2$ というのは，単振動の場合の周期 $\tau_0$ の 2 倍の時間まで，という意味ですよ。）
ライブラリの import と設定
# NumPy も使います
import numpy as np
# Matplotlib でグラフを描きます
import matplotlib.pyplot as plt
# mathtext font の設定
plt.rcParams['mathtext.fontset'] = 'cm'
# SciPy による2階常微分方程式の数値解法
# solve_ivp
from scipy.integrate import solve_ivp
# グラフを SVG で Notebook にインライン表示させる設定
%config InlineBackend.figure_formats = ['svg']
運動方程式に出てくる円周率 $\pi$ や三角関数 $\sin\theta$ は NumPy で定義されているものを使います。
import numpy as np
として import しているので，NumPy で定義されているものを使う場合には np. をつけます。
例えば，円周率 $\pi = $ np.pi，三角関数 $\sin\theta = $ np.sin(theta) などです。
連立常微分方程式の右辺を定義
2階常微分方程式を数値的に解くためには，1階連立常微分方程式に書き直します。
$T = $ t，$\theta = $ y[0]，$\dot{\theta} = $ y[1] として，
\begin{eqnarray}
\frac{d\theta}{dT} = \frac{d}{dt} {\tt y[0]} &=& F_1(t, y) = {\tt y[1]} \\
\frac{d^2\theta}{dT^2} = \frac{d}{dt} {\tt y[1]} &=& F_2(t, y) = -4 \pi^2 \sin({\tt y[0]})
\end{eqnarray}
# 連立微分方程式の右辺
# scipy.integrate.solve_ivp() は
# dy/dt = F(t, y) の形を解く
def F(t, y):
# solve.ivp() に渡す関数の引数の順番に注意。t が先
# たとえ t に依存しなくても，必ずこう書く。
# 以下のようなインデント（行頭の字下げ）部分が定義
# Python ではインデントには意味があるのでしたね。
theta = y[0]
dottheta = y[1]
F1 = dottheta
F2 = -4 * np.pi**2 * np.sin(theta)
return [F1, F2]
数値解の精度を確認
初期条件 $T = 0$ で
\begin{eqnarray}
\theta(0) &=& \theta_0 \\
\dot{\theta}(0) &=& 0
\end{eqnarray}
まず，$\theta_0 = 80^{\circ}$ の場合に，数値計算の精度について確認しておく。
SciPy の scipy.integrate.solve_ivp() では，数値計算の精度に関係するのは rtol と atol である。
マニュアルによると，デフォルトでは（rtol atol を指定しないと） rtol = 1e-3, atol = 1.e-6。
# 初期条件
T0 = 0
# 80°をラジアンに
theta0 = np.radians(80)
dottheta0 = 0
# 計算範囲
T1 = 2
N = 100
# 計算範囲：T0 から T1 までを N 等分したリストを作成
# このリストの時刻ごとに計算結果を出力する
t_list = np.linspace(T0, T1, N+1)
sol = solve_ivp(F, [T0, T1], [theta0, dottheta0],
t_eval = t_list)
print('デフォルト, V(T=2) = %.10f'
%(sol.y[1][-1]))
# 精度を変えて結果を確認。
for TOL in [1e-8, 1e-9, 1e-10, 1e-11, 1e-12, 1e-13]:
sol = solve_ivp(F, [T0, T1], [theta0, dottheta0],
t_eval = t_list,
rtol = TOL,
atol = TOL)
# 最後の値を表示し，誤差を確認。
# Python ではリストの最後（最後尾）の値は [-1] で参照する
print('TOL = %.0e, V(T=2) = %.10f'
%(TOL, sol.y[1][-1]))
デフォルトでは小数点以下1桁程度の精度しかないことがわかる。
上の結果から TOL = 1.e-12 で小数点以下 10 桁程度の精度があるとわかる。以後の計算は，これくらいで行う。
# 初期条件と計算範囲
T0 = 0
dottheta0 = 0
T1 = 2
# ちょっと N が大きいがあとで意味がわかる
N = 200000
t_list = np.linspace(T0, T1, N+1)
# 初期条件 θ0 = 80° をラジアンに
th0 = 80
theta0 = np.radians(th0)
sol80 = solve_ivp(F, [T0, T1], [theta0, dottheta0],
t_eval = t_list,
rtol = 1.e-12,
atol = 1.e-12)
solve_ivp() による数値解は sol80 に格納されています。値を参照するには以下のように。
# t_eval すなわち t_list は
sol80.t
# theta すなわち y[0] は
sol80.y[0]
# dottheta すなわち y[1] は
sol80.y[1]
計算結果のグラフ
数値計算できたら，結果をグラフにしてみます。横軸に（規格化された）時間 $T =$ sol80.t，縦軸に角度 $\theta =$ sol80.y[0] をとってグラフにします。
# ax を使う際の最初のおまじない
fig, ax = plt.subplots()
ax.plot(sol80.t, sol80.y[0]);
縦軸の単位を度に変えたグラフ
縦軸の振れ角をラジアンから度に変えたグラフを描きます。度からラジアンへの変換は np.radians() でした。ラジアンから度へは np.degrees() です。
また，初期条件を凡例に記し，サイエンティフィックなグラフらしく grid（格子線）等をつけてみます。
参考：凡例や横軸縦軸のラベルに $\LaTeX$ 記法を使っています。きれいな数式用書体で表示されます。$\LaTeX$ 記法では \$ で挟んだ間に数式や \ （バックスラッシュ）ではじまるコマンドを書きます。一部，\ （バックスラッシュ）が誤認識されてしまう場合があるので，安全のために文字列の前に r をつける。
# ax を使う際の最初のおまじない
fig, ax = plt.subplots()
# LaTeX 記法
# \ を正しく認識してもらうために r をつける
key = r"$\theta_0 = 80^{\circ}$"
ax.plot(sol80.t, np.degrees(sol80.y[0]), label = key);
# 横軸縦軸のラベル。
# LaTeX 記法
# \ を正しく認識してもらうために r をつける
ax.set_xlabel("規格化された時間 $T$")
ax.set_ylabel(r"振れ角 $\theta$ (°)")
# グリッド（格子線）の表示。私は点線が好み。
ax.grid(ls = 'dotted')
# 凡例の表示
ax.legend();
振れ角の初期値を変えて計算
$\theta_0 = 80^{\circ}$ の場合は数値計算できたので，$\theta_0 = 70^{\circ}, 60^{\circ}, 45^{\circ}$，そして比較のために，ほぼ単振動と思われる $\theta_0 = 1^{\circ}$ の場合も計算します。
$\theta_0 = 80^{\circ}$ の場合のコードを4回分コピペして… というのもなんですので，for 文を使って繰り返し処理してみます。
# 計算結果を保存しておくリスト
# sols に [th0, theta, V] の順に保存しておく
sols = []
th0s = [80, 70, 60, 45, 1]
for th0 in th0s:
theta0 = np.radians(th0)
sol = solve_ivp(F, [T0, T1], [theta0, dottheta0],
t_eval = t_list,
rtol = 1.e-12,
atol = 1.e-12)
sols.append([th0, sol.y[0], sol.y[1]])
$\theta$ のグラフ
計算結果をあわせてグラフに。
# ax を使う際の最初のおまじない
fig, ax = plt.subplots()
for sol in sols:
# 凡例 label の設定。LaTeX 表記は $ で囲む。
key = r"$\theta_0 = %2d^{\circ}$" % sol[0]
plt.plot(t_list, np.degrees(sol[1]), label = key)
# 横軸縦軸のラベル。
ax.set_xlabel("規格化された時間 $T$")
ax.set_ylabel(r"振れ角 $\theta$ (°)")
# グリッド（格子線）の表示。私は点線が好み。
ax.grid(ls = 'dotted')
# 横軸の表示範囲
ax.set_xlim(0, 2)
# 凡例の表示
ax.legend();
○練習：$\dot{\theta}$ のグラフ
$\dot{\theta}$ の計算結果もグラフにしてみよ。
# ax を使う際の最初のおまじない
fig, ax = plt.subplots()
for sol in sols:
...
...
...
# 横軸縦軸のラベル。
...
...
# グリッド（格子線）の表示。
...
# 横軸の表示範囲
...
# 凡例の表示
...
周期は速度の向きが変わる時刻から…
単振り子の周期については，$\dot{\theta}(t) = 0$ となる $t$ を数値的に解いて求めることができる。以下でやってましたね。
- 参考：○練習：単振り子の周期
ここでは，もう少し原始的な方法で考えてみる。
初速度 $\dot{\theta}(0) = 0$ ではじまる振り子の運動は，半周期ごとに $\dot{\theta} = 0$ となるはずである。実際の数値計算では，刻み幅
$$h \equiv \frac{T_1 -T_0}{N}$$
を使って離散的な時刻 $T_i = T_0 + i h$ での値を求めているので，厳密に $\dot{\theta}=0$ となる瞬間が得られるとは限らない。したがって，速度の向きが変わる時刻，
つまり
$$\dot{\theta}(T_i) > 0, \quad \dot{\theta}(T_{i+1}) \leq 0$$
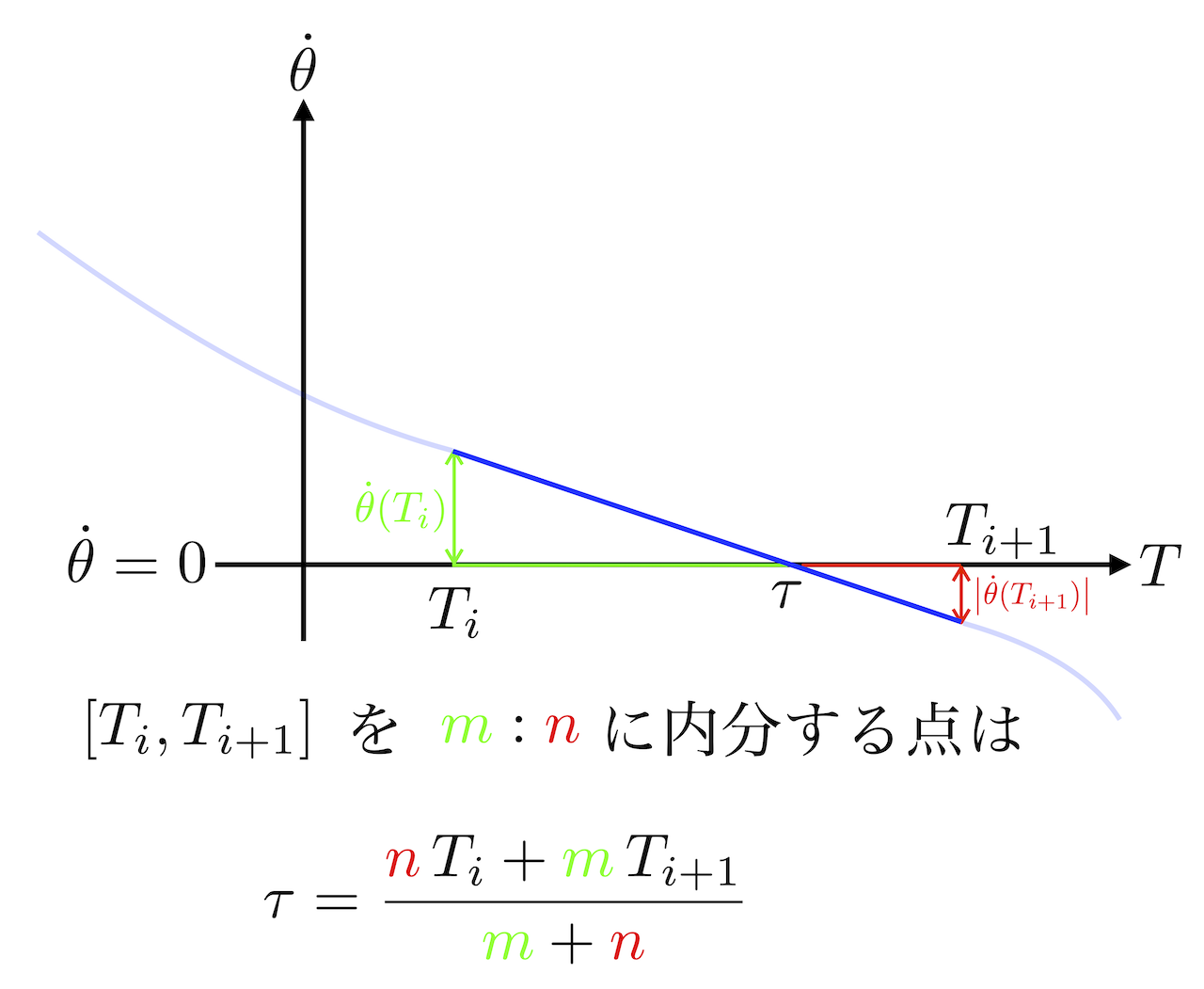
となる時刻 $T_i$ および $T_{i+1}$ を探し，$\dot{\theta}(\tau) = 0$ となる時刻である周期 $\tau$ を，$T_i$ と $T_{i+1}$ を $\dot{\theta} (T_i) : \bigl| \dot{\theta}(T_{i+1})\bigr|$ に内分する点として以下のように求めることにする。
$$ \tau = \frac{\bigl| \dot{\theta}(T_{i+1})\bigr|\,T_i + \dot{\theta} (T_i)\, T_{i+1}}{\dot{\theta} (T_i) + \bigl| \dot{\theta}(T_{i+1})\bigr|}$$
ただグラフを描くためだけなら，N = 200000 などという大きな値をとる必要はないのだが，このように速度の向きが変わる瞬間をとらえたいときには，なるべく刻み幅を小さくすると良いはず。
このような理由で N の値を大きくしていることは理解しておこう。
では，$\theta_0 = 80^{\circ}$ の場合の数値計算の結果を使い，上で述べた方法で周期を求めてみる。
# theta0 = 80 の数値解を確認
sol80 = sols[0]
# 振幅
print(sol80[0])
# theta
print(sol80[1])
# dot theta
print(sol80[2])
print('θ0 = %2d° のとき，' % sol80[0], end = '') # end = '' なら改行せず
for i in range(1, N-1):
# i の繰り返しはこのインデント
# 速度の向きが変わるかどうかを判定
if (sol80[2][i] > 0) & (sol80[2][i+1] <= 0):
# if が成り立つ時の実行文はこのインデント
# 内分点の式から周期を計算
m = sol80[2][i]
n = abs(sol80[2][i+1])
tau = (n*t_list[i] + m*t_list[i+1])/(m + n)
print('周期 τ = %.7f' % tau)
以上の結果から，例えば振れ角の初期条件を $\theta_0 = 80^{\circ}$ とした時の周期は $\tau = 1.1374926$，すなわち単振動の場合の周期
$$\tau_0 = 2\pi \sqrt{\frac{\ell}{g}}$$
の $1.1374926$ 倍だということになる。
○練習：単振り子の周期
では本題。$\theta_0 = 10^{\circ}$ から $10^{\circ}$ きざみで $90^{\circ}$ まで， $T = 0$ から $ T = 2$ まで解き，その結果から振れ角 $\theta_0$ に対する周期 $\tau$ を求めてみよ。
また，横軸に振れ角 $\theta_0$，縦軸に周期 $\tau$ をとったグラフを描け。
グラフにするためには振幅 th0 のリストと，振幅の各要素に対応する周期 tau のリストが必要ですよ。
th0 のリスト作成例は以下の通り：
# [10, 20, ...] と全部手書きするより楽？
th0s = [10*i for i in range(1, 10)]
th0s
それぞれの $\theta_0$ に対する周期 $\tau$ もリストにするんですよ。
大学の力学等でも，単振り子の運動方程式は，振れ角が非常に小さくて $\sin\theta \simeq \theta$ と近似できるときの話しかしないかもしれない。
近似しないときには，単振り子の運動方程式は解析的に解けないからである。
ここでは，2階常微分方程式を数値的に解くことによって，単振り子の周期は振れ角に依存することがわかった。
「振り子の等時性は成り立たない」
ということを理解できた！という意味で，これは重要な経験だと思うが，いかがでしょうか。