回転系における単振り子の運動方程式を,「一般にベクトルを微分するときは,成分だけでなく基本ベクトルも微分する必要があるのだ」という立場で計算してみる。以下のページを参考に。
単振り子の運動方程式
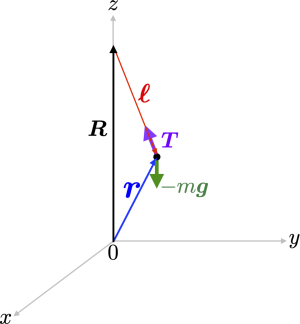
単振り子のおもりの質量を $m$,位置ベクトルを $\boldsymbol{r}$ とすると,おもりには鉛直下向きの重力 $-m \boldsymbol{g}$ と,(伸び縮みしない質量が無視できる)ワイヤーからの張力 $\boldsymbol{T}$ がはたらいているので,運動方程式は
$$m \frac{d^2 \boldsymbol{r}}{dt^2} = -m \boldsymbol{g} + \boldsymbol{T}$$
ここで $\boldsymbol{g}$ は重力加速度ベクトルであり,鉛直上向きを $z$ 軸にとっているので
$$\boldsymbol{g} = (0, 0, g)$$
$z$ 成分の $g$ は重力加速度の大きさをあらわす。
単振り子の支点(固定点)の位置ベクトルを $\boldsymbol{R} = (0, 0, R)$ とし,支点からの相対位置ベクトル $\boldsymbol{\ell}$ を
$$\boldsymbol{\ell}\equiv \boldsymbol{r} -\boldsymbol{R}$$
と定義する。支点は固定されているので $$\dfrac{dR}{dt} = 0$$
また,単振り子は伸び縮みしないので $$\ell \equiv \sqrt{\boldsymbol{\ell}\cdot\boldsymbol{\ell}} = \mbox{const.}$$
運動方程式の両辺に相対位置ベクトル $\boldsymbol{\ell}$ を外積してやり,$\boldsymbol{\ell}$ に対する微分方程式の形にしてやると
$$m \boldsymbol{\ell}\times \frac{d^2 \boldsymbol{\ell}}{dt^2} = -m \boldsymbol{\ell}\times\boldsymbol{g} + \boldsymbol{\ell}\times\boldsymbol{T}$$
張力 $\boldsymbol{T}$ は $\boldsymbol{\ell}$ に平行であるから(向きは反対)
$$\boldsymbol{\ell}\times\boldsymbol{T} = \boldsymbol{0}$$
従って,運動方程式は最終的に
$$ \boldsymbol{\ell}\times \ddot{\boldsymbol{\ell}} = -\boldsymbol{\ell}\times\boldsymbol{g} \tag{1}$$
となる。張力 $\boldsymbol{T}$ があらわれないようまとめたのがポイントであり,このようにベクトル形で表すことによって,この運動方程式は慣性系でも回転系のような非慣性系でもそのままの形で成り立つ。これも大事なポイント。
慣性系における単振り子の運動
慣性系においては一定である基本ベクトル $\boldsymbol{e}_x, \boldsymbol{e}_y, \boldsymbol{e}_z$ の表記は省略して成分のみを表記することにして,
\begin{eqnarray}
\boldsymbol{g} &=& (0, 0, g) \\
\boldsymbol{\ell} &=& (\ell_x, \ell_y, \ell_z) \\
&=& (x, y, z -R) \\
&\equiv& ( \ell \sin\theta \cos\phi, \ell \sin\theta \sin\phi, -\ell \cos\theta) \quad (z -R < 0)
\end{eqnarray}
まず,運動方程式 $(1)$ の $z$ 成分は,左辺が
\begin{eqnarray}
(\boldsymbol{\ell}\times \ddot{\boldsymbol{\ell}})_z &=& \ell_x\,\ddot{\ell}_y -\ell_y\,\ddot{\ell}_x \\
&=& \frac{d}{dt} \left( \ell_x\, \dot{\ell}_y -\ell_y\, \dot{\ell}_x\right)\\
&=& \frac{d}{dt} \left(\ell_x^2 \frac{d}{dt} \left(\frac{\ell_y}{\ell_x} \right) \right)\\
&=& \ell^2 \frac{d}{dt} \left( \sin^2\theta\, \dot{\phi}\right)
\end{eqnarray}
であり,右辺は
\begin{eqnarray}
-\left(\boldsymbol{\ell}\times\boldsymbol{g}\right)_z &=& -(\ell_x\, g_y -\ell_y\, g_x) = 0
\end{eqnarray}
従って左辺と右辺を等号でつなぐと,$(1)$ 式の $z$ 成分は
\begin{eqnarray}
\frac{d}{dt} \left( \sin^2\theta\, \dot{\phi}\right) &=& 0 \\
\therefore\ \ \sin^2\theta\, \dot{\phi} &=& \mbox{const.} \tag{2}
\end{eqnarray}
条件として,単振り子の運動は $x = 0, y = 0$ (支点の鉛直方向真下)を通るとすると,そのとき $\theta = 0$ であるから $(2)$ 式の右辺の定数 $\mbox{const.} $ はゼロ。従って
\begin{eqnarray}
\sin^2\theta\, \dot{\phi} &=& 0 \\
\therefore\ \ \dot{\phi} &=& 0 \\
\therefore\ \ \phi &=& \mbox{const.}
\end{eqnarray}
となる。このことは,振動面が一定であることを意味する。以後は簡単のために
\begin{eqnarray}
\phi &=& \mbox{const.} \Rightarrow 0 \\
\therefore \ \ \ell_x &\Rightarrow& \ell \sin\theta \\
\ell_y &\Rightarrow&0
\end{eqnarray}
として計算を続ける。
運動方程式 $(1)$ の $x$ 成分は,左辺が
$$(\boldsymbol{\ell}\times \ddot{\boldsymbol{\ell}})_x = \ell_y\, \ddot{\ell}_z -\ell_z\, \ddot{\ell}_y = 0$$
右辺も
$$-\left(\boldsymbol{\ell}\times\boldsymbol{g}\right)_x = -(\ell_y\, g_z -\ell_z\, g_y) = 0$$
となる。最後に運動方程式 $(1)$ の $y$ 成分は,左辺が
\begin{eqnarray}
(\boldsymbol{\ell}\times \ddot{\boldsymbol{\ell}})_y &=& \ell_z\, \ddot{\ell}_x -\ell_x\, \ddot{\ell}_z\\
&=& \frac{d}{dt} \left(\ell_z\, \dot{\ell}_x -\ell_x\, \dot{\ell}_z \right)\\
&=& \frac{d}{dt} \left(\ell_z^2 \frac{d}{dt} \left(\frac{\ell_x}{\ell_z} \right) \right)\\
&=& \frac{d}{dt} \left(\ell^2 \cos^2\theta\, \frac{d}{dt} \left(\frac{\sin\theta}{-\cos\theta} \right) \right)\\
&=& -\ell^2 \ddot{\theta}
\end{eqnarray}
右辺は
\begin{eqnarray}
-\left(\boldsymbol{\ell}\times\boldsymbol{g}\right)_y &=& -(\ell_z\, g_x -\ell_x\, g_z) \\
&=& \ell g\,\sin\theta
\end{eqnarray}
左辺と右辺を等号で結ぶと,最終的に運動方程式 $(1)$ の $y$ 成分は
\begin{eqnarray}
-\ell^2 \ddot{\theta} &=& \ell g\,\sin\theta \\
\therefore\ \ \ddot{\theta} &=& -\frac{g}{\ell} \sin\theta
\end{eqnarray}
この式の導出については,以下のページも参考に。
回転系における単振り子の運動
回転系においても運動方程式は同じ $(1)$ 式である。回転系のような非慣性系においても,ベクトル形で書かれた $(1)$ 式をそのまま使って計算をすすめるのがこのページの方針。
ただし,$\boldsymbol{\ell}$ は,慣性系に対して一定の角速度ベクトル $\boldsymbol{\omega}$ で回転する回転系の基本ベクトル $\boldsymbol{e}_{x’}, \boldsymbol{e}_{y’}, \boldsymbol{e}_{z’}$ を使って以下のように表される:
$$\boldsymbol{\ell} = \ell_{x’} \,\boldsymbol{e}_{x’} + \ell_{y’}\, \boldsymbol{e}_{y’} + \ell_{y’}\, \boldsymbol{e}_{y’} $$
回転系であるから
\begin{eqnarray}
\dot{\boldsymbol{e}}_{x’} &=& \boldsymbol{\omega}\times \boldsymbol{e}_{x’} \\
\dot{\boldsymbol{e}}_{y’} &=& \boldsymbol{\omega}\times \boldsymbol{e}_{y’} \\
\dot{\boldsymbol{e}}_{z’} &=& \boldsymbol{\omega}\times \boldsymbol{e}_{z’}
\end{eqnarray}
このへんの事情については,若干表記が異なるが以下のページにまとめている。
ベクトルの微分の際には,成分の微分だけでなく基本ベクトルも微分する必要があるのだということに注意して計算をするめると,
\begin{eqnarray}
\ddot{\boldsymbol{\ell}} &=& \ddot{\ell}_{x’}\,\boldsymbol{e}_{x’} + \ddot{\ell}_{y’}\,\boldsymbol{e}_{y’}+\ddot{\ell}_{z’}\,\boldsymbol{e}_{z’} \\
&& + 2 (\dot{\ell}_{x’}\,\dot{\boldsymbol{e}}_{x’} + \dot{\ell}_{y’}\,\dot{\boldsymbol{e}}_{y’}+\dot{\ell}_{z’}\,\dot{\boldsymbol{e}}_{z’}) \\
&& + \ell_{x’} \,\ddot{\boldsymbol{e}}_{x’} + \ell_{y’} \,\ddot{\boldsymbol{e}}_{y’}+\ell_{z’} \,\ddot{\boldsymbol{e}}_{z’} \\
&=& \ddot{\ell}_{x’}\,\boldsymbol{e}_{x’} + \ddot{\ell}_{y’}\,\boldsymbol{e}_{y’}+\ddot{\ell}_{z’}\,\boldsymbol{e}_{z’} \\
&& + 2\boldsymbol{\omega}\times(\dot{\ell}_{x’}\,\boldsymbol{e}_{x’} +\dot{\ell}_{y’}\,\boldsymbol{e}_{y’}+{\color{blue}{\dot{\ell}_{z’}\,\boldsymbol{e}_{z’}}}) \\
&& + {\color{blue}{ \boldsymbol{\omega}\times (\boldsymbol{\omega} \times \boldsymbol{\ell})}}
\end{eqnarray}
地球自転による遠心力の効果 ${\color{blue}{\boldsymbol{\omega}\times (\boldsymbol{\omega} \times \boldsymbol{\ell})}}$ と,コリオリの力のうちの速度の鉛直成分の寄与の項 ${\color{blue}{\dot{\ell}_{z’}\,\boldsymbol{e}_{z’}}}$ は他に比べて小さいので無視すると,
\begin{eqnarray}
\ddot{\boldsymbol{\ell}} &\simeq&\ddot{\ell}_{x’}\,\boldsymbol{e}_{x’} + \ddot{\ell}_{y’}\,\boldsymbol{e}_{y’}+\ddot{\ell}_{z’}\,\boldsymbol{e}_{z’} +2\boldsymbol{\omega}\times(\dot{\ell}_{x’}\,\boldsymbol{e}_{x’} +\dot{\ell}_{y’}\,\boldsymbol{e}_{y’})
\end{eqnarray}
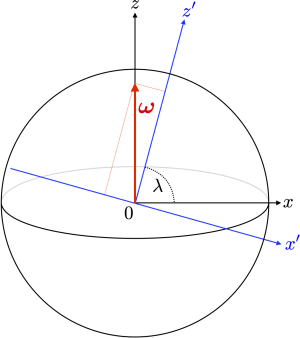
図のように,慣性系の $xy$ 平面を赤道面とし,緯度(北緯)$\lambda$ の地点の鉛直上向きを $z’$ 軸とすると,
\begin{eqnarray}
\boldsymbol{R} &=& R \,\boldsymbol{e}_{z’} \\
\boldsymbol{g} &=& g\, \boldsymbol{e}_{z’} \\
\boldsymbol{\omega} &=& -\omega\,\cos\lambda\, \boldsymbol{e}_{x’} + \omega\,\sin\lambda\, \boldsymbol{e}_{z’} \\
\therefore\ \ \boldsymbol{\omega}\times \boldsymbol{e}_{x’} &=& \omega\,\sin\lambda\, \boldsymbol{e}_{y’} \\
\boldsymbol{\omega}\times \boldsymbol{e}_{y’} &=& -\omega\,\sin\lambda\, \boldsymbol{e}_{x’}-\omega\,\cos\lambda\, \boldsymbol{e}_{z’}\\
\end{eqnarray}
\begin{eqnarray}
\therefore\ \ \ddot{\boldsymbol{\ell}} &\simeq& (\ddot{\ell}_{x’} -2\omega \dot{\ell}_{y’}\sin\lambda)\,\boldsymbol{e}_{x’} \\
&& + (\ddot{\ell}_{y’} +2\omega \dot{\ell}_{x’}\sin\lambda)\,\boldsymbol{e}_{y’} \\
&& + (\ddot{\ell}_{z’} -2\omega \dot{\ell}_{y’}\cos\lambda)\,\boldsymbol{e}_{z’} \\
&\equiv& \ddot{\ell}_{x’} \,\boldsymbol{e}_{x’} + \ddot{\ell}_{y’} \,\boldsymbol{e}_{y’}+\ddot{\ell}_{z’} \,\boldsymbol{e}_{z’}
\end{eqnarray}
運動方程式 $(1)$ の $z’$ 成分は,左辺が
\begin{eqnarray}
(\boldsymbol{\ell}\times\ddot{\boldsymbol{\ell}})_{z’} &=&
\ell_{x’}\,\ddot{\ell}_{y’} -\ell_{y’} \,\ddot{\ell}_{x’} \\
&=&
\ell_{x’}\left( \ddot{\ell}_{y’} +2\omega \dot{\ell}_{x’}\sin\lambda\right)
-\ell_{y’}\left( \ddot{\ell}_{x’} -2\omega \dot{\ell}_{y’}\sin\lambda\right)\\
&=& \frac{d}{dt} \left\{\ell_{x’}^2 \frac{d}{dt}\left(\frac{\ell_{y’}}{\ell_{x’}} \right) +\omega\left(\ell_{x’}^2+\ell_{y’}^2\right)\sin\lambda\right\}\\
&=& \ell^2 \, \frac{d}{dt}\left\{ \sin^2\theta’ \dot{\phi}’ + \omega \sin^2\theta’ \, \sin\lambda\right\}
\end{eqnarray}
ここで,
\begin{eqnarray}
\ell_{x’} &=& \ell \sin\theta’ \,\cos\phi’ \\
\ell_{y’} &=& \ell \sin\theta’ \,\sin\phi’
\end{eqnarray}
とおいた。右辺は
\begin{eqnarray}
-\left(\boldsymbol{\ell}\times \boldsymbol{g}\right)_{z’} &=& -\left(\ell_{x’}\,g_{y’} -\ell_{y’} \,g_{x’} \right) \\
&=& 0
\end{eqnarray}
従って左辺と右辺を等号でむすぶと,運動方程式 $(1)$ の $z’$ 成分から得られる式は
\begin{eqnarray}
\frac{d}{dt}\left\{ \sin^2\theta’ \dot{\phi}’ + \omega \sin^2\theta’ \, \sin\lambda\right\} &=& 0 \\
\therefore\ \ \sin^2\theta’ \dot{\phi}’ + \omega \sin^2\theta’ \, \sin\lambda &=& \mbox{const.} \tag{3}
\end{eqnarray}
条件として,単振り子の運動が $x’ = 0, y’ = 0$ を通るとすると,そのとき $\theta’ = 0$ であるから $(3)$ 式の右辺の定数はゼロ。従って
\begin{eqnarray}
\dot{\phi}’ + \omega \, \sin\lambda &=& 0 \\
\therefore\ \ \frac{d\phi’}{dt} &=& -\omega\, \sin\lambda
\end{eqnarray}
回転系で見ると,単振り子の振動面は一定ではない。緯度(北緯)$\lambda$ の地点では単位時間あたり $\omega\, \sin\lambda$ だけ,地球自転と逆向きに回転する。このようにして,フーコーの振り子の振動面が回転することが示された。