電磁気学の練習問題。ガウスの法則を使って,面対称な電荷密度がつくる電場を求める。
ガウスの法則を使った求め方
$x = 0$ の $yz$ 平面に対して面対称な電荷密度は $\rho(|x|)$ のように書かれる。ポアソン方程式
$$\nabla^2 \phi = – \frac{1}{\varepsilon_0} \rho(|x|)$$
から,静電ポテンシャル $\phi$ もまた面対称 $\phi = \phi(|x|)$ とみなすことができるだろう。このとき,$\xi \equiv \sqrt{x^2} = |x|$ として
\begin{eqnarray}
\boldsymbol{E} &=& – \nabla \phi(\xi) = – \frac{d\phi(\xi)}{d\xi} \nabla \xi\\
&\equiv& E_{\xi} (\xi) \nabla \xi\\
E_x &=& E_{\xi}(\xi) \frac{x}{|x|} \\
E_y &=& 0 \\
E_z &=& 0
\end{eqnarray}
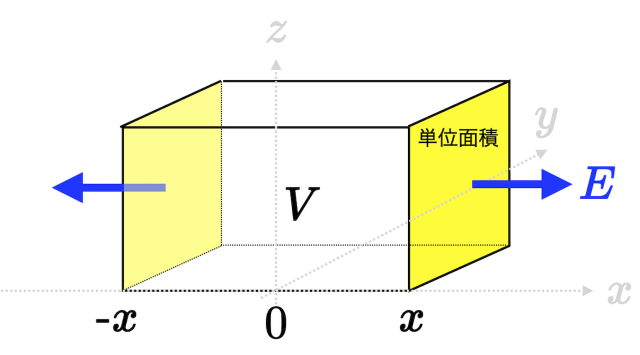
次に,図のような直方体を $V$ としてガウスの法則を体積積分すると
$$\iiint_V (\nabla\cdot\boldsymbol{E}) dV = \frac{1}{\varepsilon_0} \iiint_V \rho dV$$
右辺の積分は,この体積内の全電荷 $Q_{\xi}$ で書ける。
$$\iiint_V \rho dV = \int_{-x}^{x} \rho(|x|) dx \equiv Q_{\xi}$$
左辺はガウスの定理により,黄色く塗られた部分での面積積分に帰着して…
$$\iiint_V (\nabla\cdot\boldsymbol{E}) dV = \int_S \boldsymbol{E}\cdot\boldsymbol{n} dS = 2 E_{\xi}$$
両辺を等しいとおいて
\begin{eqnarray}
2 E_{\xi} &=& \frac{Q_{\xi}}{\varepsilon_0} \\
E_{\xi} &=& \frac{Q_{\xi}}{2 \varepsilon_0} \\
\therefore\ \ E_x &=& \frac{Q_{\xi}}{2 \varepsilon_0} \frac{x}{|x|}
\end{eqnarray}
ガウスの法則に頼らずに
$$
\boldsymbol{E} = \frac{1}{4\pi\varepsilon_0}
\iiint \frac{\rho(|x’|) \left(\boldsymbol{r}-\boldsymbol{r}’\right)}{|\boldsymbol{r}-\boldsymbol{r}’|^3} dV’
$$
を直接積分しても同じ答えが求められる。こちらに書いてある。