Maxima で領域の塗りつぶしと回転体の表示 に書いた Maxima で領域を塗りつぶす例の追記。
当時は,塗りつぶした後に explicit(f(x), x, x0, x1) ができなくて,追加の線は parametric で描く などと嘯いていたが,以下のように filled_func = false とすれば塗りつぶし終了でその後は explicit(f(x), x, x0, x1) できます。
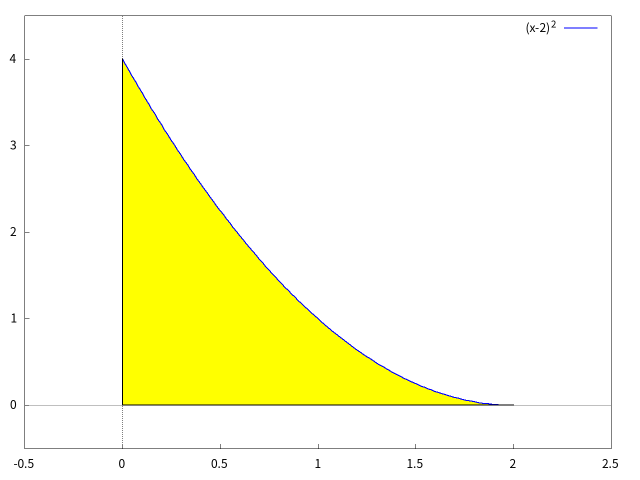
陽関数で表される曲線で囲まれた領域を塗りつぶす例
$\ \ $放物線 $y = (x-2)^2$ と,$x$ 軸 ($y = 0$),$y$ 軸とで囲まれた領域を Maxima の draw2d() で塗りつぶす。
まず,領域の上限と下限を表す陽関数を定義する。
f(x):= (x - 2)**2$
g(x):= 0$
draw2d(
font = "Arial", font_size = 18,
/* 陽関数の曲線を滑らかにするためにはこの数値を大きめに */
nticks = 30,
/* x 軸 y 軸の表示範囲の設定。*/
xrange = [-0.5, 2.5], xaxis=true,
yrange = [-0.5, 4.5], yaxis=true,
/* 塗りつぶす色の指定。*/
fill_color = yellow,
/* 上の線。y = f(x) を filled_func に代入。*/
filled_func = f(x),
/* 下の線。y = g(x) を 0 < x < 2 の範囲で描く。*/
explicit(g(x), x, 0, 2),
/* 塗りつぶし終了 */
filled_func = false,
/* 線の太さを 2 にしてメリハリをつけて */
line_width = 2,
/* 上の線。y = f(x) */
color = blue, key = "(x-2)^2",
explicit(f(x), x, 0, 2),
/* 下の線。y = g(x) */
color = black, key = "",
explicit(g(x), x, 0, 2),
/* x = 0 (y 軸) */
color = black, key = "",
parametric(0, t, t, 0, 4),
file_name = region-fig1,
dimensions = [1280,960],
terminal = 'png
)$
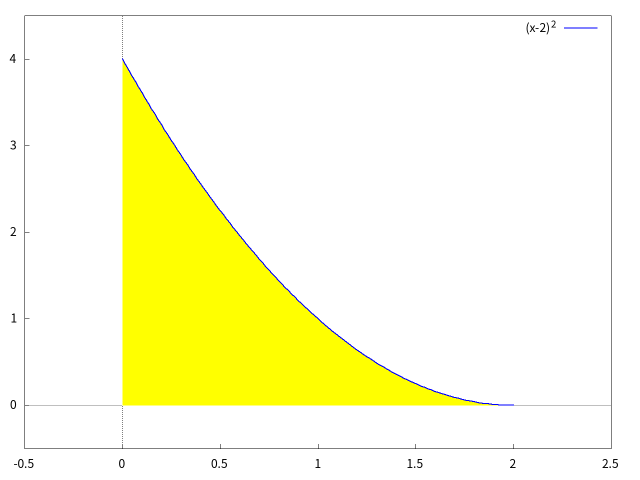
region を指定して塗りつぶす例(陽関数を使って)
region() を使うと,陽関数だけでなく陰関数も使った不等式で領域を指定して塗りつぶすことができます。
たとえば,上の例の黄色で塗りつぶされた領域は,$ 0 < x < 2$(従って $g(0) < y < f(0)$)の範囲で $y < f(x)$ の領域であるとあらわすことができます。これをグラフィックオブジェクト region() を使って以下のように表します。
region(y < f(x), x, 0, 2, y, g(0), f(0))
f(x):= (x - 2)**2$
g(x):= 0$
draw2d(
font = "Arial", font_size = 18,
/* 陽関数の曲線を滑らかにするためにはこの数値を大きめに */
nticks = 30,
/* x 軸 y 軸の表示範囲の設定。*/
xrange = [-0.5, 2.5], xaxis=true,
yrange = [-0.5, 4.5], yaxis=true,
/* 塗り残しがあるようなら値を大きくする */
x_voxel = 30, y_voxel = 30,
/* 塗りつぶす色の指定 */
fill_color = yellow,
/* 塗りつぶす領域の指定 */
region(y < f(x), x, 0, 2, y, g(0), f(0)),
/* 線の太さを 2 にしてメリハリをつけて */
line_width = 2,
/* 上の線。y = f(x) */
color = blue, key = "(x-2)^2",
explicit(f(x), x, 0, 2),
file_name = region-fig2,
dimensions = [1280,960],
terminal = 'png
)$
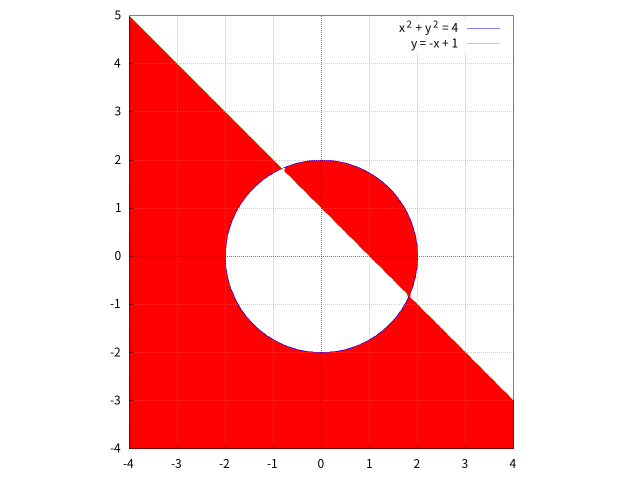
region を指定して塗りつぶす例(陰関数も使って)
$y < f(x) \equiv -x + 1$ かつ $g(x, y) \equiv x^2 + y^2 > 4$,または $y > f(x)$ かつ $g(x, y) < 4$ の領域を塗りつぶす例。
f(x):= -x + 1$
g(x, y):= x**2 + y**2$
draw2d(
font = "Arial", font_size = 18,
/* グリッドや座標軸が塗りつぶされないように */
user_preamble = "set grid front;",
/* 縦横比。*/
proportional_axes = xy,
/* x 軸 y 軸の表示 */
xaxis = true, yaxis = true,
/* 陽関数の曲線を滑らかにするためにはこの数値を大きめに */
nticks = 50,
/* 陰関数の曲線を滑らかにするためにはこの数値を大きめに */
ip_grid = [200, 200],
/* 領域の塗り残しがあるようならこの数値を大きめに */
/* ただしけっこう時間がかかるようになるよ */
x_voxel = 100, y_voxel = 100,
region((g(x, y) - 4)*(y - f(x)) <= 0, x, -4, 4, y, -4, 5),
/* 陰関数表示の円 */
key = "x^2 + y^2 = 4", color = 2,
implicit(g(x, y) - 4 = 0, x, -4, 4, y, -4, 4),
/* 陽関数表示の直線 */
key = "y = -x + 1", color = 3,
explicit(f(x), x, -4, 4),
/* region を svg にするとファイルサイズが巨大になるので */
file_name = region-fig3,
dimensions = [1280,960],
terminal = 'png
)$
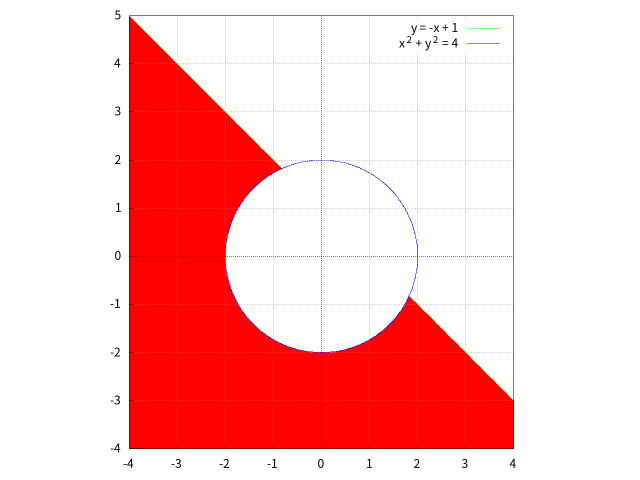
$y < f(x) \equiv -x + 1$ かつ $g(x, y) \equiv x^2 + y^2 > 4$,つまり「直線の下で円の外部」の領域を塗りつぶす例。
f(x):= -x + 1$
g(x, y):= x**2 + y**2$
draw2d(
font = "Arial", font_size = 18,
/* グリッドや座標軸が塗りつぶされないように */
user_preamble = "set grid front;",
/* 縦横比。*/
proportional_axes = xy,
/* x 軸 y 軸の表示 */
xaxis = true, yaxis = true,
/* 陽関数の曲線を滑らかにするためにはこの数値を大きめに */
nticks = 50,
/* 陰関数の曲線を滑らかにするためにはこの数値を大きめに */
ip_grid = [200, 200],
/* 領域の塗り残しがあるようならこの数値を大きめに */
/* ただしけっこう時間がかかるようになるよ */
x_voxel = 50, y_voxel = 50,
region(y - f(x) <= 0, x, -4, 4, y, -4, 5),
/* 陽関数表示の直線 */
key = "y = -x + 1", color = 3,
explicit(f(x), x, -4, 4),
/* 面倒なので円の内部を白で塗りつぶす */
/* 円の内部の直線も塗りつぶされて見えない */
key = "",
fill_color = white,
region(g(x, y)-4 <= 0, x, -4, 4, y, -4, 5),
/* 陰関数表示の円 */
key = "x^2 + y^2 = 4", color = 2,
implicit(g(x, y) - 4 = 0, x, -4, 4, y, -4, 4),
/* region を svg にするとファイルサイズが巨大になるので */
file_name = region-fig4,
dimensions = [1280,960],
terminal = 'png
)$