(そのうち修正されるかもしれないので)本日閲覧時点で,Wikipedia 日本語版の「ケプラー方程式」の項と,英語版「Kepler’s equation」の項で,ベッセル関数を使ったフーリエ級数解が微妙に異なる件。
追記: 2023-02-27
以下の件は,離心率の定義が英語版に合うように修正され,微妙な差異は解消されたようです。
- Wikipedia 日本語版の「ケプラー方程式」
Kepler’s equation – Wikipediaのフーリエ級数解
Kepler’s equation is
$$ M = E – e \sin E$$
Fourier series expansion (with respect to $M$ ) using Bessel functions is
$$ E = M + \sum_{m=1}^{\infty} \frac{2}{m} J_m(m e) \sin(m M)$$
ケプラー方程式 – Wikipediaのフーリエ級数解
$$ M = E + \epsilon \sin E$$
通常はこの形の方程式をケプラー方程式と呼んでいる。
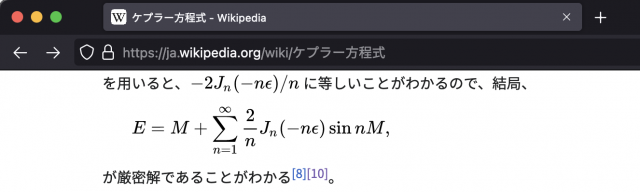
結局
$$E = M + \sum_{n=1}^{\infty} \frac{2}{n} J_n(-n \epsilon) \sin n M$$が厳密解であることがわかる。
違うのか違わないのか
一瞬,ベッセル関数の中身の正負が異なるので,え,えーっ!ベッセル関数は $n$ が奇数なら奇関数,$n$ が偶数なら偶関数だったよなぁ… これじゃあ答えが違うことになるぞ… などと思ったが,よく見ると最初のケプラー方程式で $\sin E$ の前の符号が異なる。つまり,
$$ \epsilon \Rightarrow – e$$
とすれば同じ式。Wikipedia 日本語版の記事がなぜ,ケプラー方程式について非標準的な表記をしたのか不明。
「ケプラー方程式|天文学辞典」でも
$$u(t) – e \sin u(t) = M(t)$$
だし,私の記事「ケプラー方程式を数値的に解いてケプラーの第2法則を視覚的に確認する」のケプラー方程式の導出の項でも,$e$ を離心率とすれば
$$u – e \sin u = \frac{2\pi}{T} t$$
となることが導かれている。