ここでは,赤方偏移を統一的に理解する方法に従って,
I. 重力場中の光の伝播は,ヌル測地線で与えられる
II. 4元速度 $u^{\mu}$ の観測者が観測する光の振動数は $\omega = – k_{\mu} u^{\mu}$ で与えられる
という2つの原理原則から,シュバルツシルト時空中を動径方向に自由落下運動する光源による光のドップラー効果の式を導く。
シュバルツシルト時空中を動径方向に伝播する光
今回は,静止光源と自由落下運動する光源の2つから光が放出されるので,それを区別して表記する。
測地線方程式は別ページ「シュバルツシルト時空中の光の伝播」で解いているから,その結果を使うと,静止光源からの光の4元波動ベクトル $k_{\mu} = g_{\mu\nu} \,k^{\nu}$ について
$$k_{\mu} = \left(k_0, k_1, 0, 0 \right) = \left(-\omega_c, \ \pm \frac{\omega_c}{1 – \frac{r_g}{r}}, \ 0, \ 0 \right)$$
複号 \(\pm\) は,動径方向外向きに伝播する光に対してプラス,内向きの光に対してマイナスをとる。
動径方向に自由落下運動する光源からの光の4元波動ベクトルは上と区別して $k’_{\mu}$ とし,
$$k’_{\mu} = \left(k’_0, k’_1, 0, 0 \right) = \left(-\omega’_c, \ \pm \frac{\omega’_c}{1 – \frac{r_g}{r}}, \ 0, \ 0 \right)$$
シュバルツシルト時空中の静止観測者・静止光源
静止観測者の4元速度 $u^{\mu}$ は
$$u^{\mu} = \left(u^0, 0, 0, 0\right) = \left(\frac{1}{\sqrt{1 – \frac{r_g}{r}}}, 0, 0, 0\right)$$
静止光源からの光 \(k_{\mu}\) を,位置 $r$ で静止している観測者が観測したときの振動数 \(\omega\) は
$$\omega = – k_{\mu} u^{\mu} = \frac{\omega_c}{\sqrt{1 – \frac{r_g}{r}}}$$
特に,$r = r_1$ に静止している光源の振動数は,光源静止観測者が光源と同じ位置で観測するのであるから
$$\omega_1 \equiv \omega(r_1) = \frac{\omega_c}{\sqrt{1 – \frac{r_g}{r_1}}}$$
また,自由落下運動する光源からの光 $k’_{\mu}$ を,位置 $r$ で静止している観測者が観測したときの振動数 \(\omega’ \) は
$$\omega’ = – k’_{\mu} u^{\mu} = \frac{\omega’_c}{\sqrt{1 – \frac{r_g}{r}}}$$
シュバルツシルト時空中を動径方向に自由落下運動する光源
シュバルツシルト時空中を動径方向に自由落下運動する光源の4元速度 $\bar{u}^{\mu}$ は,別ページ「シュバルツシルト時空中を動径方向に自由落下運動する観測者」で計算したように,$r = r_i\ (> r)$ で静止しているという初期条件を課すと,
$$\bar{u}^{\mu} = \left(\frac{ \sqrt{1 – \frac{r_g}{r_i}}}{1 – \frac{r_g}{r}}, -\sqrt{\frac{r_g}{r} – \frac{r_g}{r_i}}, 0, 0\right) $$
この運動する光源から $r=r_1$ で放出された光の振動数 \(\bar{\omega}’_1\) は,光源静止観測者(光源と同じ4元速度で運動する観測者)が光源と同じ位置で観測するのであるから,
\begin{eqnarray}
\bar{\omega}’_1 &=& – k’_{\mu}(r_1)\, \bar{u}^{\mu}(r_1) \\
&=& \omega’_c \frac{ \sqrt{1 – \frac{r_g}{r_i}}}{1 – \frac{r_g}{r_1}} \pm \frac{\omega’_c}{1 – \frac{r_g}{r_1}} \sqrt{\frac{r_g}{r_1} – \frac{r_g}{r_i}} \\
&=& \frac{\omega’_c}{1 – \frac{r_g}{r_1}} \left(\sqrt{1 – \frac{r_g}{r_i}} \pm \sqrt{\frac{r_g}{r_1} – \frac{r_g}{r_i}}\right)
\end{eqnarray}
ここでは,簡単のために \(r = r_1\) における静止光源からの振動数と自由落下運動する光源からの振動数は等しいとする。
\begin{eqnarray}
\omega_1 &\equiv& \bar{\omega}’_1 \\
\therefore\ \ \frac{\omega_c}{\sqrt{1 – \frac{r_g}{r_1}}} &=& \frac{\omega’_c}{1 – \frac{r_g}{r_1}} \left(\sqrt{1 – \frac{r_g}{r_i}} \pm \sqrt{\frac{r_g}{r_1} – \frac{r_g}{r_i}}\right) \\
\therefore\ \ \omega’_c &=& \omega_c \frac{\sqrt{1 – \frac{r_g}{r_1}}}{\sqrt{1 – \frac{r_g}{r_i}} \pm \sqrt{\frac{r_g}{r_1} – \frac{r_g}{r_i}}}
\end{eqnarray}
重力場中を運動する光源によるドップラー効果
光源が静止観測者に近づく場合
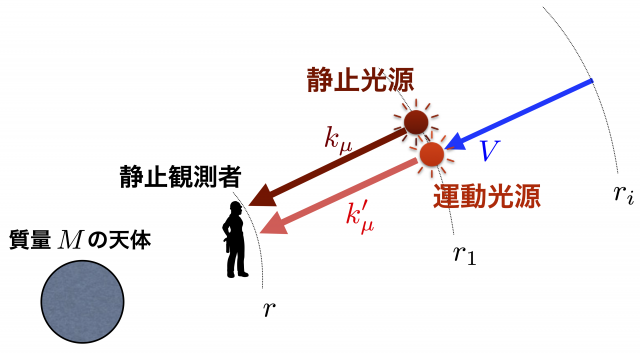
自由落下運動する光源が位置 $r\ (< r_1) $ で静止している観測者に近づく場合は,$r_g < r < r_1 < r_i$ となり,光は内向き,つまり複号 \(\pm\) の \(-\) をとる。
したがって,$r = r_1$ の静止光源からの光を位置 $r\ (< r_1) $ で静止観測者が観測する場合の振動数 \(\omega\) と,自由落下運動で近づく光源からの光を観測する場合の振動数 \(\omega’\) との比は,
\begin{eqnarray}
\frac{\omega’}{\omega}
&=& \frac{\omega’_c}{\omega_c} \\
&=& \frac{\sqrt{1 – \frac{r_g}{r_1}}}{\sqrt{1 – \frac{r_g}{r_i}} – \sqrt{\frac{r_g}{r_1} – \frac{r_g}{r_i}}}\\
&=&\frac{\sqrt{1 – \frac{r_g}{r_i}} + \sqrt{\frac{r_g}{r_1} – \frac{r_g}{r_i}}}{\sqrt{1 – \frac{r_g}{r_1}}} > 1
\end{eqnarray}
となり,自由落下運動して近づいてくる光源からの光の振動数 $\omega’$ のほうが,静止光源からの光の振動数 $\omega$ よりドップラー効果によって大きくなることがわかる。
光源が静止観測者から遠ざかる場合
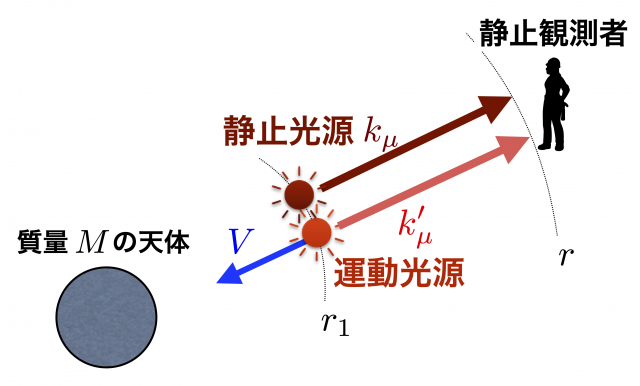
逆に,自由落下運動する光源が位置 $r\ (> r_1) $ で静止している観測者から遠ざかる場合は,$r_g < r_1 < r, \ \ r_1 < r_i$ となり,光は外向き,つまり複号 \(\pm\) の \(+\) をとる。
このとき,$r = r_1$ の静止光源からの光を位置 $r\ (< r_1) $ で静止観測者が観測する場合の振動数 \(\omega\) と,自由落下運動で近づく光源からの光を観測する場合の振動数 \(\omega’\) との比は,
\begin{eqnarray}
\frac{\omega’}{\omega}
&=& \frac{\omega’_c}{\omega_c} \\
&=& \frac{\sqrt{1 – \frac{r_g}{r_1}}}{\sqrt{1 – \frac{r_g}{r_i}} + \sqrt{\frac{r_g}{r_1} – \frac{r_g}{r_i}}}< 1
\end{eqnarray}
となり,自由落下運動して遠ざかる光源からの光の振動数 $\omega’$ のほうが,静止光源からの光の振動数 $\omega$ よりドップラー効果によって小さくなることがわかる。
光のドップラー効果の式との整合性
さて,本サイトでは「ローレンツ変換によらない赤方偏移の統一的理解」において,光のドップラー効果の式は,(特殊相対論でのみ有効な)ローレンツ変換を使わずに求めることができることを示している。
光源が近づく場合の光のドップラー効果の式
特に,静止光源からの振動数を \(\omega\),運動する光源からの振動数を \(\omega’\) と表記すると,観測者が3次元的な速さ $V$ で光源に近づく場合の光のドップラー効果の式
$$ \omega’ = \omega \sqrt{\frac{1+V}{1-V} } $$
は,特殊相対論的状況のみならず,その導出方法の一般性から,重力がある一般相対論的な状況においても同様に有効である。
動径方向に自由落下運動する光源の3次元的速さ $V$
動径座標 $r=r_1$ の地点の静止光源からみると,目の前を通過する瞬間の自由落下運動する光源の速さ $V$ は,「シュバルツシルト時空中を動径方向に自由落下運動する観測者」に記載のように,4元速度の合成則
$$\bar{u}^{\mu} = \frac{1}{\sqrt{1 – V^2}} u^{\mu} + \frac{V}{\sqrt{1 – V^2}} e^{\mu} $$
を使うと,それぞれの4元速度の内積がローレンツ因子を表すこと
$$\frac{1}{\sqrt{1-V^2}} = – u_{\mu} \bar{u}^{\mu}$$
から $V$ を求めることができ,
\begin{eqnarray}
V &=& \frac{ \sqrt{ \frac{r_g}{r_1} – \frac{r_g}{r_i} } }{ \sqrt{1-\frac{r_g}{r_i}} }
\end{eqnarray}
となる。
ドップラー効果の式に代入して…
上記の $V$ をドップラー効果の式に代入すると,
\begin{eqnarray}
\frac{\omega’}{ \omega} &=& \sqrt{\frac{1+V}{1-V} } \\
&=& \frac{1+V}{\sqrt{1-V^2}} \\
&=& \frac{1+\frac{ \sqrt{ \frac{r_g}{r_1} – \frac{r_g}{r_i} } }{ \sqrt{1-\frac{r_g}{r_i}} }}{\sqrt{1-\frac{ { \frac{r_g}{r_1} – \frac{r_g}{r_i} } }{{1-\frac{r_g}{r_i}} }}}\\
&=&\frac{{ \sqrt{1-\frac{r_g}{r_i}} }+{ \sqrt{ \frac{r_g}{r_1} – \frac{r_g}{r_i} } }}{\sqrt{{{1-\frac{r_g}{r_i}} }-{ { \left(\frac{r_g}{r_1} – \frac{r_g}{r_i}\right) } }}}\\
&=&\frac{{ \sqrt{1-\frac{r_g}{r_i}} }+{ \sqrt{ \frac{r_g}{r_1} – \frac{r_g}{r_i} } }}{\sqrt{{{1-\frac{r_g}{r_1}} }}}
\end{eqnarray}
となり,(当然の結果ではあるが)上記で求めた $\displaystyle \frac{\omega’}{\omega}$ と一致している。
光源が遠ざかる場合も同様
速さ $V$ で光源が遠ざかる場合も同様で,
$$ \omega’= \omega \sqrt{\frac{1-V}{1+V} }$$
に速さ $V$ を代入すればよい。