世の中の教科書では光のドップラー効果はどのように説明されているか。例えば,「相対性理論」(中野董夫著,岩波書店)の p. 87 あたり等を参考にして,ローレンツ変換にもとづいた光のドップラー効果の説明について,おさらいする。簡単のために \(c=1\) とする。
光の伝播をあらわす4元波数ベクトル
観測者 \(A\) の静止慣性系である \(S\) 系では,光の4元波数ベクトルの成分は
$$k^{\mu} = (k^0, k^1, k^2, k^3) = (\omega, k_x, k_y, k_z)$$
\(A\) に対して速さ \(V\) で \(x\) 方向に運動する観測者 \(B\) の静止慣性系である \(S’\) 系では
$$k^{\mu’} = (k^{0^{\prime}}, k^{1^{\prime}}, k^{2^{\prime}}, k^{3^{\prime}}) = (\omega’, k’_x, k’_y, k’_z)$$
ローレンツ変換
あらかじめ念のために言っておくが,ローレンツ変換に基づいた以下の説明は,重力がない特殊相対論的状況でのみ有効である。重力がある場合は,そもそもローレンツ変換が使えないため,別途理屈を考える必要がある。
\(S\) 系の座標 \(x^{\mu}\) と \(S’\) 系の座標 \(x^{\mu’}\) の間の座標変換は,以下のローレンツ変換で与えられる。
\begin{eqnarray}
t’ &=& \frac{t -V x}{\sqrt{1-V^2}} \\
x’ &=& \frac{x -V t}{\sqrt{1-V^2}} \\
y’ &=& y \\
z’ &=& z
\end{eqnarray}
この逆変換(\(S\) 系の座標 \(x^{\mu}\) を \(S’\) 系の座標 \(x^{\mu’}\) で表すこと)は
\begin{eqnarray}
t &=& \frac{t’ + V x’}{\sqrt{1-V^2}} \\
x &=& \frac{x’ + V t’}{\sqrt{1-V^2}}
\end{eqnarray}
光の位相は座標系によらない不変量である
\begin{eqnarray}
\omega t -\boldsymbol{k}\cdot\boldsymbol{r} &=& \omega t -k_x x -k_y y -k_z z \\
&=& \omega’ t’-k_x’ x’ -k_y’ y’ -k_z’ z’
\end{eqnarray}
ということから,4元波数ベクトルの成分も,ローレンツ変換で変換されることが導かれ,
\begin{eqnarray}
\omega’ &=& \frac{\omega -V k_x}{\sqrt{1-V^2}} \tag{1}\\
k_x’ &=& \frac{k_x -V \omega}{\sqrt{1-V^2}} \tag{2}\\
k_y’ &=& k_y \\
k_z’ &=& k_z
\end{eqnarray}
逆変換は
\begin{eqnarray}
\omega &=& \frac{\omega’ + V k_x’}{\sqrt{1-V^2}} \tag{3}\\
k_x &=& \frac{k_x’ + V \omega’}{\sqrt{1-V^2}} \tag{4}\\
\end{eqnarray}
4次元添字表記のローレンツ変換
ちなみに,座標を $x^{\mu} = \left(x^0, x^1, x^2, x3\right)$ のように4次元の添字で表したときのローレンツ変換は \(c = 1\) として
\begin{eqnarray}
x^{0^{\prime}} &=& \frac{x^0 -V x^1}{\sqrt{1-V^2}} \\
x^{1^{\prime}} &=& \frac{x^1 -V x^0}{\sqrt{1-V^2}} \\
x^{2^{\prime}} &=& x^{2} \\
x^{3^{\prime}} &=& x^{3}
\end{eqnarray}
光の4元波数ベクトルの成分も同様に,成分を $k^{\mu} = \left(k^0, k^1, k^2, k^3\right)$ のように4次元の添字で表して
\begin{eqnarray}
k^{0^{\prime}} &=& \frac{k^0 -V k^1}{\sqrt{1-V^2}} \\
k^{1^{\prime}} &=& \frac{k^1 -V k^0}{\sqrt{1-V^2}} \\
k^{2^{\prime}} &=& k^{2} \\
k^{3^{\prime}} &=& k^{3}
\end{eqnarray}
逆変換は
\begin{eqnarray}
k^{0} &=& \frac{k^{0^{\prime}} +V k^{1^{\prime}}}{\sqrt{1-V^2}} \\
k^{1} &=& \frac{k^{1^{\prime}} +V k^{0^{\prime}}}{\sqrt{1-V^2}}
\end{eqnarray}
光のヌル条件
簡単のために,光は \(xy\) 平面上を伝播すると仮定して,\(k_z = k_z’ = 0\) とする。
ヌル条件 \(\displaystyle \eta_{\mu\nu} k^{\mu} k^{\nu} = \eta_{\mu\nu} k^{\mu’} k^{\nu’} = 0\) より
\begin{eqnarray}
-\omega^2 + k_x^2 + k_y^2 &=& 0 \\
-\left(\omega’ \right)^2 + \left(k_x’ \right)^2 +\left(k_y’ \right)^2 &=&0
\end{eqnarray}
したがって,光の4元ベクトルの空間成分は以下のように書くことができる。
\begin{eqnarray}
k_x = \omega \cos\theta, &\quad& k_y = \omega \sin \theta\\
k_x’ = \omega’ \cos\theta’, &\quad& k_y’ = \omega’ \sin \theta’
\end{eqnarray}
ここで \(\theta\) は観測者 \(A\) が観測する光の進行方向と \(x\) 方向とのなす角,\(\theta’\) は観測者 \(B\) が観測する光の進行方向と \(x’\) 方向とのなす角である。
\(A\) とともに静止している光源からの光を運動する \(B\) が観測する場合
\((3)\) 式から
\begin{eqnarray}
\omega &=& \frac{\omega’ + V k_x’}{\sqrt{1-V^2}} \\
&=& \frac{\omega’ + V \omega’ \cos\theta’}{\sqrt{1-V^2}} \\
&=& \omega’ \frac{1 + V \cos \theta’}{\sqrt{1-V^2}} \\
\therefore\ \ \omega’ &=& \omega\frac{\sqrt{1-V^2}}{1 + V \cos \theta’} \tag{5}
\end{eqnarray}
光源静止系での振動数 \(\omega\) をあらためて \(\omega_0\) ,観測者 \(B\) の観測する振動数 \(\omega’\) をあらためて \(\omega_{\rm obs}\) とすると
$$\omega_{\rm obs}= \omega_0\frac{\sqrt{1-V^2}}{1 + V \cos \theta’} $$
特に,観測者が光源から遠ざかる場合は \(\theta’ = 0\) とすると
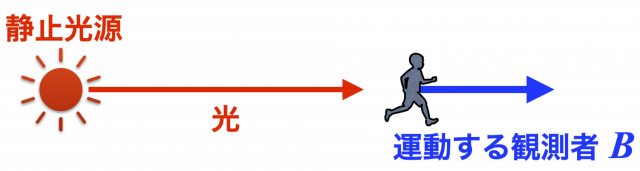
$$\omega_{\rm obs}= \omega_0\frac{\sqrt{1-V^2}}{1 + V} = \omega_0 \sqrt{\frac{1-V}{1+V} } < \omega_0$$
となり,振動数は小さく,したがって波長が伸びて観測される。
また,\((4)\) 式から(\((5)\) 式も使って… )
\begin{eqnarray}
k_x = \omega \cos\theta &=& \frac{k’_x + V \omega’}{\sqrt{1-V^2}} \\
&=& \frac{\omega’ \cos\theta’ + V \omega’}{\sqrt{1-V^2}} \\
&=& \omega’ \frac{\cos\theta’ + V}{\sqrt{1-V^2}} \\
\therefore\ \ \cos\theta &=& \frac{\omega’}{\omega} \frac{\cos\theta’ + V}{\sqrt{1-V^2}} \\
&=& \frac{\sqrt{1-V^2}}{1 + V \cos \theta’}\frac{\cos\theta’ + V}{\sqrt{1-V^2}} \\
&=& \frac{\cos\theta’ + V}{1 + V \cos \theta’} \tag{6}
\end{eqnarray}
\(B\) とともに運動している光源からの光を静止している \(A\) が観測する場合
\((1)\) 式から
\begin{eqnarray}
\omega’ &=& \frac{\omega -V k_x}{\sqrt{1-V^2}} \\
&=& \frac{\omega -V \omega \cos\theta}{\sqrt{1-V^2}} \\
&=& \omega \frac{1 -V \cos \theta}{\sqrt{1-V^2}} \\
\therefore\ \ \omega &=& \omega’\frac{\sqrt{1-V^2}}{1 -V \cos \theta} \tag{7}
\end{eqnarray}
光源静止系での振動数 \(\omega’\) をあらためて \(\omega_0\) ,観測者 \(A\) の観測する振動数 \(\omega\) をあらためて \(\omega_{\rm obs}\) とすると
$$\omega_{\rm obs}= \omega_0\frac{\sqrt{1-V^2}}{1 -V \cos \theta} $$
特に,光源が観測者から遠ざかる場合は \(\theta = \pi\) であり,
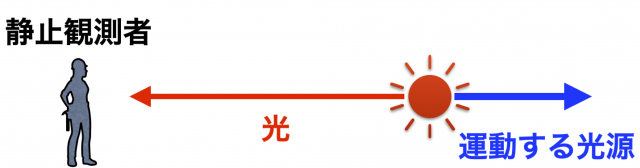
$$\omega_{\rm obs}= \omega_0\frac{\sqrt{1-V^2}}{1 + V} = \omega_0 \sqrt{\frac{1-V}{1+V} } < \omega_0$$
となり,振動数は小さく,したがって波長が伸びて観測される。
以上のことから,光源が動くか観測者が動くかにかかわらず,互いの間の相対速度によって光のドップラー効果が起こることがわかる。
また,\((2)\) 式から(\((7)\) 式も使って… )
\begin{eqnarray}
k’_x = \omega’ \cos\theta’ &=& \frac{k_x -V \omega}{\sqrt{1-V^2}} \\
&=& \frac{\omega \cos\theta -V \omega’}{\sqrt{1-V^2}} \\
&=& \omega \frac{\cos\theta -V}{\sqrt{1-V^2}} \\
\therefore\ \ \cos\theta’ &=& \frac{\omega}{\omega’} \frac{\cos\theta -V}{\sqrt{1-V^2}} \\
&=& \frac{\sqrt{1-V^2}}{1 -V \cos \theta}\frac{\cos\theta -V}{\sqrt{1-V^2}} \\
&=& \frac{\cos\theta -V}{1 -V \cos \theta} \tag{8}
\end{eqnarray}
\((6)\) 式および \((8)\) 式が,静止観測者の観測する光の入射角 $\theta$ と運動する観測者の観測する光の入射角 $\theta’$ の関係を表す。観測者の運動によって $\theta’ \neq \theta$ となる現象が光行差である。