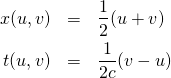• abst-sample-utf8.tex
• abstract.sty
• plot1.pdf （サンプル用。上記 tex ファイルで includegraphics されている）

上記ファイルを（必要ならマウス右ボタンクリックで）ダウンロードしてください。

サンプル LaTeX ファイル

\documentclass[12pt]{jarticle}
\usepackage{abstract}
% abstract.sty を この tex ファイルと同じところに置いておく。
%%% これより上は変更しないでください %%%
\usepackage{wrapfig}
\usepackage[dvipdfmx]{graphicx}
\usepackage[dvipdfmx]{color}
%%% 上のパッケージは図を使う場合のみ必要 %%%
%
\title{
地球環境防災学科　卒業論文要旨の作成例
\large{\\--- 副題がある場合はこのように記入 ---}
%% 副題が不要の場合は % \large{...} のように先頭に % をつける。
}
\author{地球環境防災学科　19S3099　苗字 名前}
\begin{document}
\maketitle

要旨作成で \LaTeX を使う場合には，
要旨作成用の \texttt{tex} ファイル（例えばこのファイル）と同じ
場所（フォルダまたはディレクトリとも言う）に
{\color{red}\texttt{abstract.sty}}を置いてタイプセットしてください。

出来上がりは，\textbf{卒業論文は1ページ}，
\textbf{修士論文は2ページ}までの{\color{blue}\textbf{PDFファイル}}で
提出してください。

グラフや図を挿入する場合は，PDF ファイルを準備し，以下のようにします。
\begin{verbatim} 
 \includegraphics[width=0.5\textwidth]{plot1.pdf}
\end{verbatim}

% 以下の例では，本文の幅の半分のサイズの図の領域を確保します。
\begin{wrapfigure}{r}{0.5\textwidth} %% 図右寄せの場合{r}
\includegraphics[width=0.5\textwidth]{plot1.pdf}
\caption{図の説明}
\end{wrapfigure}

図に文章を回り込ませるような，少し凝った配置をしたい場合は，
このファイルの例のように，
\verb|wrapfigure| 環境を使ってみるのもいいかもしれません。

要旨ですので，詳細な数式を書くスペースはありませんが，
それでもどうしても必要な場合は，以下のようにきちんと書きます。
\begin{equation}
 R_{\mu\nu}-\frac{1}{2} g_{\mu\nu} R = \frac{8\pi G}{c^4} T_{\mu\nu}
\end{equation}

それでは，頑張って卒業論文・修士論文および論文要旨を期限までに仕上げて提出してください。

弘前大学理工学部地球環境防災学科・卒業論文，
大学院理工学研究科地球環境学コース・修士論文の要旨担当からのお知らせでした。

\end{document}

出来上がり例

macOS の TeXShop で書くことを想定しているが，utf8 が処理できる環境であれば特に問題なくタイプセットできると思います。

重要：TeXShop の「環境設定…」から「設定プロファイル」を「pTex(ptex2pdf)」にしておく。

以下のファイルをダウンロードし，同じ場所において，TeXShop で sotsuron-sample-utf8.tex を開き，「タイプセット」ボタンをクリック。

• sotsuron-sample-utf8.tex
• plot1.pdf

Windows 用に Shift-JIS に変換した TeX ファイル：

• sotsuron-sample-sjis.tex

タイトルページと目次

\documentclass[a4paper,12pt]{jsreport}
\usepackage{bm}
\usepackage[dvipdfmx]{graphicx}
\usepackage{ascmac}

\title{卒論・修論を\LaTeX で書く}
\author{弘前大学理工学部地球環境防災学科\\
学籍番号　名前}
\date{2020年吉日}

\begin{document}
\maketitle
\tableofcontents

第1章

\chapter{はじめに}

最初はイントロ的なことを書く。
\section{現状と問題点}

最近の現状と問題点とか。

\section{解決策の提案}

こうしたらいい，とか。

\section{数式の書き方}

アインシュタイン方程式は以下の通りである。
\begin{equation}
R_{\mu\nu} - \frac{1}{2} g_{\mu\nu} R =
\frac{8\pi G}{c^2} T_{\mu\nu}
\end{equation}

第2章

\chapter{つぎに}

この辺から本番。

\section{文献の引用の仕方}

データは参考文献\cite{rika} にあったものを使った．
この文献\cite{ten}も参考にした。

\section{図の挿入の仕方}
\begin{figure}[h]
\begin{center}
\includegraphics[width=7cm]{./plot1.pdf}
\caption{サイン関数のグラフ}
\end{center}
\end{figure}

第3章

\chapter{最後に}

結論とか，まとめとか。
最後にいうのもなんだが，ベクトルの書き方。
\begin{itemize}
\item 普通の$\alpha$は\verb|\alpha|で書く。
\item \verb|$\vec{\alpha}$| で $\vec{\alpha}$
\item \verb|\usepackage{bm}| している場合は
\verb|$\bm{\alpha}$| で $\bm{\alpha}$
\item 並べると，$\alpha$, $\vec{\alpha}$, $\bm{\alpha}$
\end{itemize}

謝辞

\chapter*{謝辞}

謝辞には第何章とかの番号をつけなくてもよいので，そんなときは，
\verb|\chapter*{ }| という具合に書きます。

みなさん，ありがとう．(普通の人が見るのは，イントロと謝辞だけ...
という説もあるから，忘れないで書く．)

付録

\appendix
\chapter{付録があるときは}
プログラム文とかを書いてページ数を稼ぎたいときは，
以下のようにしてみます。

\begin{verbatim}
#include <iostream>
using namespace std;
int main() {
for(int i = 1; i <= 5; i++) {
cout << "こんにちは, C++ の世界! " << i << endl;
}
return 0;
}
\end{verbatim}
\verb|\usepackage{ascmac}|して\verb|screen| 環境を使うと，枠がつきます。
\begin{screen}
\begin{verbatim}
#include <iostream>
using namespace std;
int main() {
for(int i = 1; i <= 5; i++) {
cout << "こんにちは, C++ の世界! " << i << endl;
}
return 0;
}
\end{verbatim}
\end{screen}

参考文献

\begin{thebibliography}{99}
\bibitem{rika} 国立天文台編，理科年表 (丸善)
\bibitem{ten} 天文年鑑，誠文堂新光社。
\end{thebibliography}

\end{document}