一次元波動方程式に関連して,偏微分の規則について質問があったので補足。
(1) ![]()
上の一次元波動方程式を解く際,以下のような変数変換![]() を行う。
を行う。
(2) ![]()
もともと ![]() の関数である
の関数である ![]() は変数変換すると,
は変数変換すると,![]() の関数
の関数 ![]() になるので,合成関数の偏微分の規則にしたがって,
になるので,合成関数の偏微分の規則にしたがって,
(3) ![]()
変数変換の式から,
(4) ![]()
(5) ![]()
なので,
(6) ![]()
これが任意の ![]() について成り立つのだから,
について成り立つのだから,
(7) ![]()
![]() についても同様。
についても同様。
また,この変数変換の逆変換とは,![]() を
を ![]() で表すことであり,以下のようになる。
で表すことであり,以下のようになる。
(8) 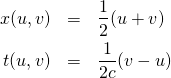
もともと ![]() の関数であった関数は
の関数であった関数は ![]() と
と![]() の関数とみなされるので,合成関数の偏微分の規則により,
の関数とみなされるので,合成関数の偏微分の規則により,
(9) ![]()
(10) ![]()
したがって,
(11) ![]()
(12) ![]()