葛西 真寿　弘前大学大学院理工学研究科

一様重力場中の単ふりこ

Maxima を使って一様重力場中の単ふりこの問題を数値的に解きます。

振幅が小さい時には単振動になり，振り子の周期は振幅に依存しないことが知られていますが，振幅が大きいときの（「十分小さい」という近似が成り立たない場合の）ふりこの周期は，振幅にどう依存するでしょうか？

単ふりこの運動方程式

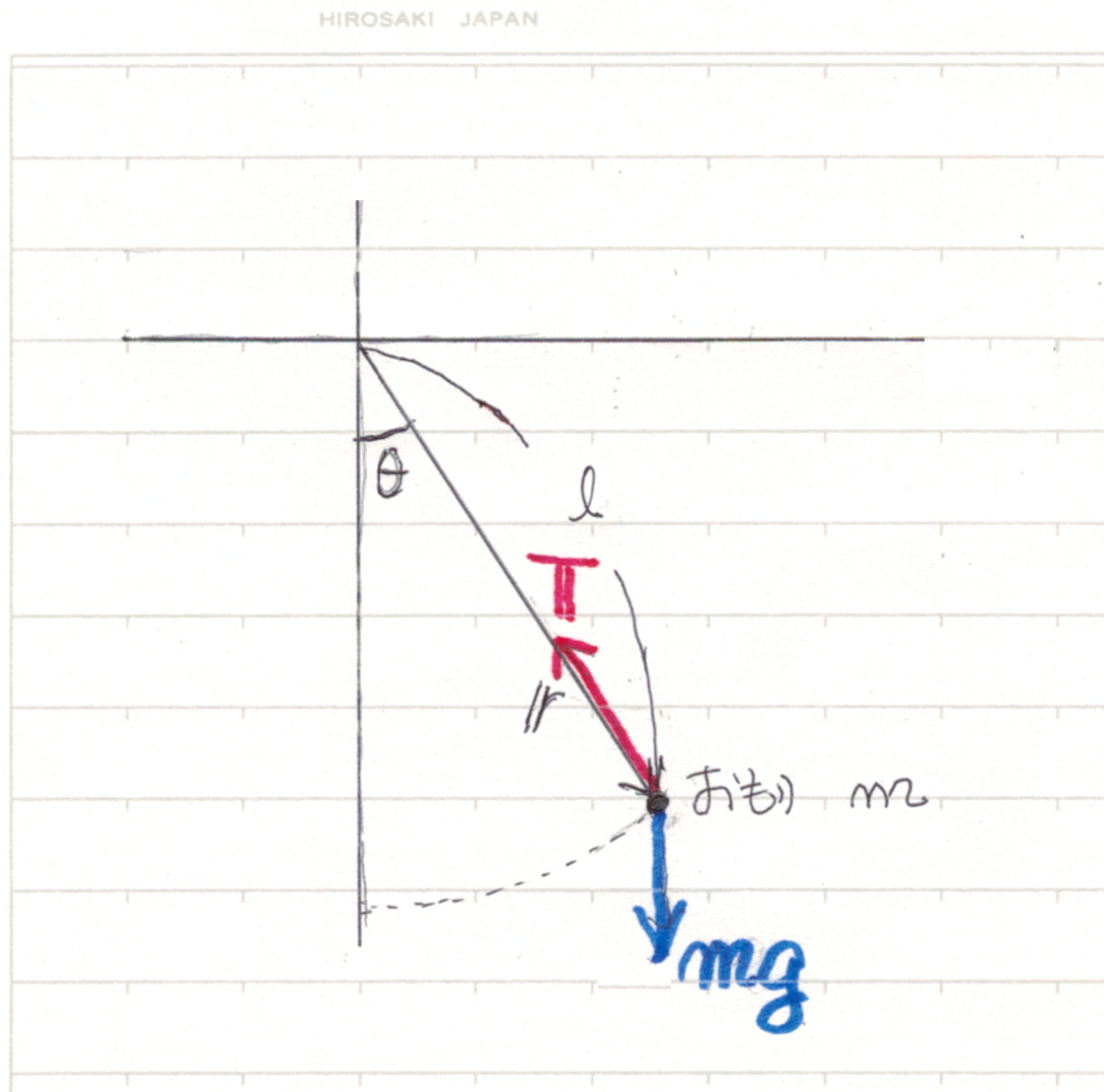
単ふりこのひもの長さを $\ell$，重力加速度の大きさを $g$，鉛直下向きからの振れ角を $\theta$ とすると，単ふりこの運動方程式は

$$ \frac{d^2\theta}{dt^2} = - \frac{g}{\ell} \sin\theta $$

となることを示す。

単ふりこ

運動方程式

（以下，Jupyter Notebook の数式表示では，3次元ベクトルをboldsymbol $\boldsymbol{r}$ のように表すと普通の $r$ と区別がつきにくい懸念があるので，$\vec{r}$ のように表すことにする。）

単ふりこの先端のおもりは，ひもの張力 $\vec{T}$ と重力 $ m\vec{g}$ を受ける。鉛直下向きを $+z$ 方向とすると $\vec{g} = (0, 0, g)$ は重力加速度ベクトル, $g$ は重力加速度の大きさである。

したがって，運動方程式は

$$m \frac{d^2\vec{r}}{dt^2} = m\vec{g} + \vec{T}$$

保存量（角運動量の鉛直成分）

この式の両辺に位置ベクトル $\vec{r}$ の外積をかける。$\vec{T} \propto - \vec{r}$ であることに注意すると，$\vec{r}\times \vec{T} = \vec{0}$ であるから，運動方程式は以下のようになる。

$$\frac{d}{dt}\left(m \vec{r}\times\frac{d\vec{r}}{dt}\right) = m \vec{r}\times\vec{g}$$

この両辺に一定のベクトルである重力加速度ベクトル $\vec{g}$ の内積をかけてやると，

$$ \frac{d}{dt}\left\{\vec{g}\cdot\left(m\vec{r}\times\frac{d\vec{r}}{dt}\right)\right\} = 0 $$

この式は，角運動量 $\displaystyle \vec{L} \equiv m \vec{r}\times\frac{d\vec{r}}{dt}$ の鉛直成分，つまり重力加速度ベクトルにそった成分が保存することを意味する。

運動が平面内に限られる理由

この式を成分で具体的に書き下すと（両辺を $m g$ で割ったのち）

$$\frac{d}{dt}\left( x \frac{dy}{dt} - y \frac{dx}{dt}\right) = \frac{d}{dt}\left\{ x^2 \frac{d}{dt}\left(\frac{y}{x}\right) \right\} = 0 $$

極座標 $$\vec{r} = (x, y, z) = (\ell \sin\theta \cos\varphi, \ell \sin\theta \sin\varphi, \ell \cos\theta) $$

を使って書くと，

$$\frac{d}{dt}\left\{ x^2 \frac{d}{dt}\left(\frac{y}{x}\right) \right\} = \ell^2 \frac{d}{dt} \left(\sin^2\theta \frac{d\varphi}{dt} \right) = 0 $$

微分してゼロということは，中身が一定であることだから，

$$ \sin^2\theta \frac{d\varphi}{dt} = \mbox{const.} \equiv l_z $$

ここで，初期条件として $t = 0$ で $\displaystyle\frac{d\varphi}{dt} = 0$ とすると，$l_z = 0$ となり常に $\displaystyle\frac{d\varphi}{dt} = 0$，つまり $\varphi = \mbox{const.}$ でありつづけることが示される。

したがって，単ふりこの運動が（慣性系では）一定の平面内に限られるのは，以下の理由による：

  • 角運動量の鉛直成分（重力加速度ベクトルに平行な成分）は保存される。
    （上記の場合は，重力加速度ベクトルの向きは $z$ 方向なので，角運動量の $z$ 成分 $L_z = m \ell^2 l_z$ が一定である。）

  • 初期条件として $L_z = 0$ とすると，ずーっと $L_z = 0$ でありつづける。
    （上記の場合は初期条件として $\displaystyle \frac{d\varphi}{dt} = 0$ とすると，ずーっと $\displaystyle \frac{d\varphi}{dt} = 0$でありつづける，つまり $\varphi = \mbox{const.}$）

  • したがって，運動は $\varphi$ が一定の平面内に限られる。

すなわち，初期条件として，$\displaystyle y = 0, \frac{dy}{dt} = 0$ とすると，以後の 単ふりこの運動は $y = 0$ の $xz$ 平面内に限られることがわかる。

最終的な運動方程式

そこでこれ以後は，$\vec{r} = (x, y, z) = (\ell\sin\theta, 0, \ell\cos\theta)$ とおく。

すると，$\vec{r}$ と外積をとった運動方程式の残りの成分のうち，$x$ 成分は $ 0 = 0$ となり， $y$ 成分は以下のようになる。

\begin{eqnarray} \frac{d}{dt} \left( z \frac{dx}{dt} - x \frac{dz}{dt} \right) &=& -x g \\ \frac{d}{dt} \left\{z^2 \frac{d}{dt}\left(\frac{x}{z}\right)\right\} &=& -x g \\ \ell^2 \frac{d}{dt} \left\{ \cos^2\theta \frac{d}{dt}\left( \frac{\sin\theta}{\cos\theta}\right) \right\} &=& - \ell g \sin\theta \\ \ell^2 \frac{d^2\theta}{dt^2} =&=& - \ell g \sin\theta \end{eqnarray}

であるから，運動方程式は最終的に

$$ \frac{d^2\theta}{dt^2} = - \frac{g}{\ell} \sin\theta $$

となる。

振幅が小さい場合

$|\theta| \ll 1$ の場合には，$\sin\theta \simeq \theta$ と近似することにより，運動方程式は

$$ \frac{d^2\theta}{dt^2} \simeq - \frac{g}{\ell} \theta$$

となり，これは単振動となる。

単振動の周期

単振動の周期 $T_0$ は

$$ T_0 = 2\pi \sqrt{\frac{\ell}{g}} $$

となり，これは初期条件で与えられる振れ幅（振幅）$\theta_0$ に依存しない。

振幅が大きい場合の周期は？

振幅が大きい，つまり $\sin\theta \simeq \theta$ と近似できない場合は，単振動ではない運動をするはずだから，ふりこの周期は一般に振幅に依存するのではないかと考えられる。

そこで，振幅 $\theta_0$ をたとえば $10$° から $90$° まで $10$° きざみで大きくしていった場合，ふりこの周期はどうなるか？　というのが問題。

無次元化された運動方程式

解析的に解けない場合は，数値的に解くことになる。そんなとき，解くべき方程式を無次元化しておくとよい。

ここでは，単振動の場合の周期 $T_0$ の2乗を運動方程式の両辺にかける。 すると，右辺は

$$- T_0^2 \times \frac{g}{\ell} \sin\theta = - 4\pi^2 \sin\theta$$

となる。また，規格化された時間 $\tau$ を

$$ \tau \equiv \frac{t}{T_0}$$

のように定義すると

$$ T_0^2 \frac{d^2}{dt^2} = \frac{d^2}{d\tau^2}$$

となるので，無次元化された運動方程式は以下のようになる。

$$ \frac{d^2\theta}{d\tau^2} = - 4\pi^2 \sin\theta$$

まず，この2階常微分方程式を数値的に解いてみる。

運動方程式の数値解

ルンゲ・クッタ法 rk()

常微分方程式系をルンゲ・クッタ法で数値的に解く rk() を使って運動方程式の数値解を求めます。

    rk ([ODE1, …, ODEm], [v1, …, vm], [init1, …, initm], domain)

Maxima のマニュアルでは以下の例が示されています。

dx/dt = 4-x^2-4*y^2     dy/dt = y^2-x^2+1
t は 0 から 4 の間, t = 0 で x が -1.25, y が 0.75 という条件: 

sol: rk([4-x^2-4*y^2, y^2-x^2+1],
        [x, y], 
        [-1.25, 0.75], [t, 0, 4, 0.02])$
plot2d([discrete, makelist([p[1], p[3]], p, sol)], 
       [xlabel, "t"], [ylabel, "y"])$

無次元化された運動方程式

$$ \frac{d^2\theta}{d\tau^2} = - 4\pi^2 \sin\theta$$

を以下のような連立1階常微分方程式の系にしてルンゲ・クッタ法で数値的に解いています。

d theta/dt = dottheta
d dottheta/dt = - 4*%pi**2*sin(theta)

まず，$\theta_0 = 60$° の場合に，刻み幅を変えてみて精度を確認してみます。

In [1]:
sol1: rk([dottheta, -4*%pi**2*sin(theta)], 
         [theta, dottheta], 
         [60*%pi/180, 0], [t, 0, 2, 0.001])$

sol2: rk([dottheta, -4*%pi**2*sin(theta)], 
         [theta, dottheta], 
         [60*%pi/180, 0], [t, 0, 2, 0.0002])$
In [2]:
print(sol1[length(sol1)][1], sol1[length(sol1)][2], sol1[length(sol1)][3])$
print(sol2[length(sol2)][1], sol2[length(sol2)][2], sol2[length(sol2)][3])$
\(2.0\) \(0.6952100567947159\) \(4.599353167586568\)
\(2.0\) \(0.6952100568756764\) \(4.599353167159691\)

刻み幅 0.001 で小数点以下9桁ほどの精度が出ていることがわかります。以後は，この刻み幅で続けます。

In [3]:
sol10: rk([dottheta, -4*%pi**2*sin(theta)], 
         [theta, dottheta], 
         [10*%pi/180, 0], [t, 0, 2, 0.001])$

sol60: rk([dottheta, -4*%pi**2*sin(theta)], 
         [theta, dottheta], 
         [60*%pi/180, 0], [t, 0, 2, 0.001])$

plot2d()

振幅 10° の場合と 60° の場合の数値解をプロットします。

In [4]:
/* Jupyter Notebook にインラインでグラフを表示させる場合，*/
/* 最初に以下のようにプロットオプションをセット。 */
set_plot_option([svg_file, "~/.maxplot.svg"])$
In [5]:
plot2d([[discrete, makelist([p[1], p[2]], p, sol10)], 
        [discrete, makelist([p[1], p[2]], p, sol60)]], 
       [xlabel,"t"],[ylabel,"y"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 1 y t discrete1 discrete1 discrete2 discrete2 -1.5 -1 -0.5 0 0.5 1 1.5 0 0.5 1 1.5 2

判断しやすいように，初期条件の振幅で規格化した数値解をプロットします。

In [6]:
data10: makelist([sol10[i][1], sol10[i][2]/sol10[1][2]], i, length(sol10))$
data60: makelist([sol60[i][1], sol60[i][2]/sol60[1][2]], i, length(sol60))$

plot2d([[discrete, data10], [discrete, data60]], 
       [xlabel, "t"], [ylabel, "θ"], grid2d,
       [legend, "振幅 10°", "振幅 60°"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 1 θ t 振幅 10° 振幅 10° 振幅 60° 振幅 60° -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0 0.5 1 1.5 2

上のグラフを見る限りでは，振幅が60°と大きくなると，周期がのびているように見えます。

もう少し定量的に調べてみます。

数値計算の答えのうち，$\dot{\theta}$ の数値解は sol10[i][3] や sol60[i][3] に格納されています。この数値解をみて，$\theta$ の値が増加から減少に転じる時刻，つまり $\dot{\theta}$ の値が正から負に転じる時刻を以下のようにして調べてみます。

In [7]:
print("振幅 10°")$
for i: 3 thru length(sol10)-1
  do(
  if (sol10[i][3] >=0) and (sol10[i+1][3] <= 0) then 
      print("周期 = ", sol10[i][1])
)$

print("振幅 60°")$
for i: 3 thru length(sol60)-1
  do(
  if (sol60[i][3] >=0) and (sol60[i+1][3] <= 0) then 
      print("周期 = ", sol60[i][1])
)$
振幅 10°
周期 = \(1.001\)
振幅 60°
周期 = \(1.073\)

問題

無次元化された運動方程式を数値的に解き，振幅 $\theta_0$ を $10$° から $90$° まで $10$° きざみで大きくしていった場合，ふりこの周期はどのように変化するかを示せ。

保存量（エネルギー保存則）

無次元化された運動方程式

$$ \frac{d^2\theta}{d\tau^2} = - 4\pi^2 \sin\theta$$

の両辺に $\displaystyle \frac{d\theta}{d\tau}$ をかけて整理すると，

$$\frac{d}{d\tau}\left\{ \frac{1}{2}\left( \frac{d\theta}{d\tau} \right)^2 - 4\pi^2 \cos\theta \right\} = 0 $$

つまり，

$$ \frac{1}{2}\left( \frac{d\theta}{d\tau} \right)^2 - 4\pi^2 \cos\theta = \mbox{const.} \equiv \varepsilon $$

という保存量が存在することがわかる。（これはエネルギー保存則です。）

$t = 0$ で $\displaystyle \theta = \theta_0, \frac{d\theta}{d\tau} = 0$ という初期条件を課すと，定数 $\varepsilon$ の値は以下のように定まる。 $$ \varepsilon = - 4\pi^2 \cos\theta_0$$

つまり，

$$\frac{d\theta}{d\tau} = \pm 2\pi \sqrt{2(\cos\theta-\cos\theta_0)}$$

これは変数分離形の微分方程式であり，$\theta$ が $0$ から $\theta_0$ までの時間の4倍が周期 $\bar{T}$ になることから，

$$ \frac{1}{2\pi} \int_0^{\theta_0} \frac{d\theta}{\sqrt{2(\cos\theta-\cos\theta_0)}} = \int_0^{\bar{T}/4} d\tau $$

すなわち

$$ \bar{T} = \frac{2}{\pi} \int_0^{\theta_0} \frac{d\theta}{\sqrt{2(\cos\theta-\cos\theta_0)}} $$

第1種完全楕円積分

ここでは，上記の積分が変数変換によって，第1種完全楕円積分

$$K(k) \equiv \int_0^{\pi/2} \frac{dt}{\sqrt{1 - k^2 \sin^2 t}}$$

で書けることを示す。

まず，分母は半角の公式を使って

\begin{eqnarray} \sqrt{2 (\cos\theta-\cos\theta_0)} &=& \sqrt{2 \left\{ \left(1-2\sin^2\frac{\theta}{2}\right) -\left(1-2\sin^2\frac{\theta_0}{2}\right) \right\} }\\ &=& 2\sqrt{\sin^2\frac{\theta_0}{2} - \sin^2\frac{\theta}{2}} \end{eqnarray}

ここで，

$$\displaystyle \sin\frac{\theta_0}{2} \equiv k, \quad \sin\frac{\theta}{2} \equiv k \sin t $$

とおくと，

\begin{eqnarray} 2\sqrt{\sin^2\frac{\theta_0}{2} - \sin^2\frac{\theta}{2}} &=& 2 k \sqrt{1 - \sin^2 t} \\ &=& 2 k \cos t \end{eqnarray}

一方，分子は

$$ \sin\frac{\theta}{2} \equiv k \sin t $$

より，

$$ d\theta = \frac{2 k \cos t}{\cos\frac{\theta}{2}} dt = \frac{2 k \cos t}{\sqrt{1-k^2 \sin^2 t}} dt $$

したがって，

\begin{eqnarray} \int_0^{\theta_0} \frac{1}{\sqrt{2(\cos\theta-\cos\theta_0)}} d\theta &=&\int_0^{\pi/2} \frac{1}{2 k \cos t} \frac{2 k \cos t}{\sqrt{1-k^2 \sin^2 t}} dt\\ &=&\int_0^{\pi/2} \frac{dt}{\sqrt{1-k^2 \sin^2 t}}\\ &\equiv& K(k) \end{eqnarray}

elliptic_kc (m)

ありがたいことに，Maxima では以下のように定義された第一種完全楕円積分

integrate(1/sqrt(1 - m*sin(x)^2), x, 0, %pi/2)

が elliptic_kc (m) として使えます。

In [8]:
K(m):= 'integrate(1/sqrt(1 - m*sin(x)^2), x, 0, %pi/2);
Out[8]:
\[\tag{${\it \%o}_{16}$}K\left(m\right):=\int_{0}^{\frac{\pi}{2}}{\frac{1}{\sqrt{1-m\,\sin ^2x}}\;dx}\]
In [9]:
k: float(sin(60*%pi/(180*2)));
Out[9]:
\[\tag{${\it \%o}_{17}$}0.5\]
In [10]:
2/float(%pi) * elliptic_kc(k**2);
Out[10]:
\[\tag{${\it \%o}_{18}$}1.073182007149365\]

問題

第1種完全楕円積分を使って書かれたふりこの周期の式を使い，振幅 $\theta_0$ を $10$° から $90$° まで $10$° きざみで大きくしていった場合，ふりこの周期はどのように変化するかを示せ。

また，運動方程式を数値的に解いて得られた結果と比較せよ。

参考：第1種完全楕円積分の数値積分

第1種完全楕円積分

$$K(m) \equiv \int_0^{\pi/2} \left[1 - m \sin^2 t \right]^{-1/2}\, dt$$

を数値積分で求めてみる。

romberg()

In [11]:
rombergtol: 1.e-12$
Knum(m):= romberg(1/sqrt(1-m*sin(x)*sin(x)), x, 0, %pi/2)$
In [12]:
print(2/float(%pi) * elliptic_kc(k**2))$
print(2/float(%pi) * Knum(k**2))$
\(1.073182007149365\)
\(1.073182007149365\)

ということから，第1種完全楕円積分は（おそらく内部的には同じことをしているのであろうと想像できますが）組み込み関数 elliptic_kc() でも，数値積分してくれる関数 romberg() を使っても，同じ答えが出るようです。