Maxima-Jupyter による数式処理とグラフ作成

葛西 真寿　弘前大学大学院理工学研究科

この Notebook では，「wxMaxima による数式処理とグラフ作成」のテキストの内容を，Jupyter Notebook 上で Maxima-Jupyter を使って説明しています。

セクションの構成は，wxMaxima 版のテキストに準じています。

Maxima-Jupyter による数式処理

基本操作

Maxima-Jupyter の起動

ターミナル等で

jupyter notebook (または jupyter-notebook)

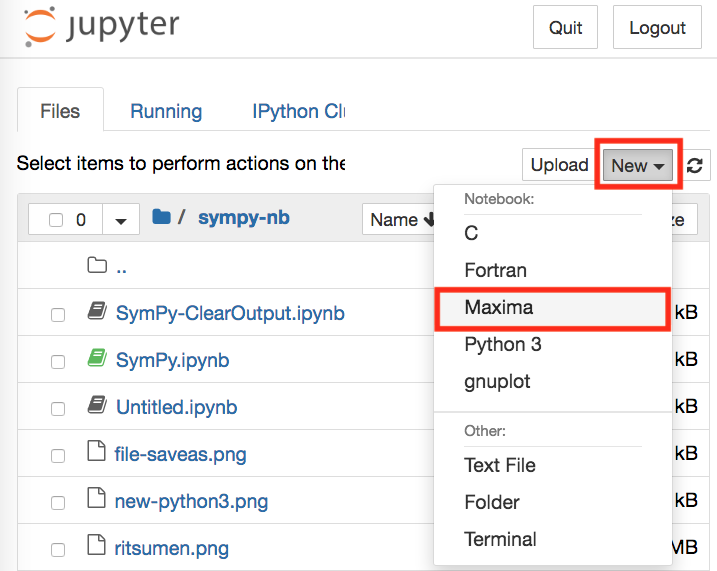
右上の「New」から 「Maxima」を選ぶ。

計算の実行と改行

計算の実行は，数値や式などを入力して最後にセミコロン ; を入力後，Shift キーを押しならが Enter キー（または Return キー）を押します。

まずは簡単なかけ算 123×456 を計算してみます。

In [1]:
123 * 456;
Out[1]:
\[\tag{${\it \%o}_{1}$}56088\]

2 の 100 乗 (2100) のような大きい数でも，厳密な結果を出力します。（^ は累乗を表します。）

In [2]:
2^100;
Out[2]:
\[\tag{${\it \%o}_{2}$}1267650600228229401496703205376\]

float 関数を使って不動小数点表示で近似値を出力させることもできます。

In [3]:
float(2^100);
Out[3]:
\[\tag{${\it \%o}_{3}$}1.26765060022823 \times 10^{+30}\]

Enter キーのみでは改行されるだけで計算が実行されません。Shift+Enter キーが入力されるまで，Maxima は式の入力が継続していると判断します。

例として，以下のような積分を計算してみます。Shift キーを忘れて Enter キーのみを押すと単に改行されます。慌てずにセミコロン ; を入力後， Shift キーを押しながら Enter キーを押すと実行します。

答えは $\int 3x^2\ dx = x^3$ です.

In [4]:
integrate(3*x^2, x)


;
Out[4]:
\[\tag{${\it \%o}_{4}$}x^3\]

計算結果の保存と読み込み

Jupyter Notebook （の Maxima-Jupyter）で計算した結果を保存するには，「File」メニューから「Save as ... 」でファイル名をつけて保存します。

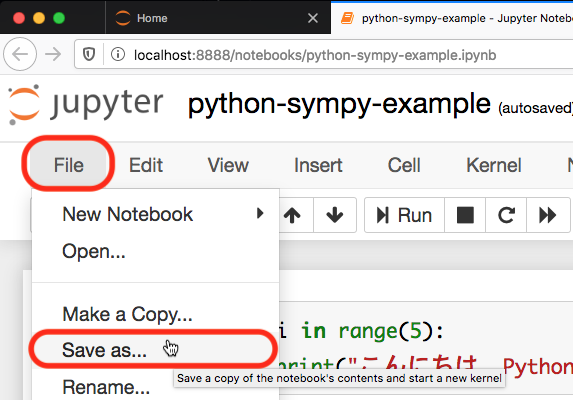
「File」メニューの真下に，なにやら四角で右上隅がかけている形のアイコンがありますが（これが「フロッピーディスク」というものであることは，20世紀の昔を知る人にしかわからないと思います），このアイコンをクリックしても保存されます。

また，「File」メニューから「Open... 」を選び，計算結果が保存された Notebook をまた利用することもできます。

表記などの約束事

Maxima の実行に際して，いくつか表記についての約束事があります。代表的なものを以下に示します。

コメント(実行に影響しない注釈)を 入れたいときは，/* ... */ でコメント部分を囲みます。

In [5]:
1 + 2 + 3;
Out[5]:
\[\tag{${\it \%o}_{5}$}6\]
In [6]:
1 + 2 /* + 3 */;
Out[6]:
\[\tag{${\it \%o}_{6}$}3\]

加法 +，減法 -，乗法 *，除法 / における優先順位は数学と同じです。優先して計算したい箇所は ( ) で 囲みます。

In [7]:
1 + 2 * 3;
Out[7]:
\[\tag{${\it \%o}_{7}$}7\]
In [8]:
(1 + 2) * 3;
Out[8]:
\[\tag{${\it \%o}_{8}$}9\]

ただし，大カッコ [ ] や中カッコ { } は優先順位の指定には用いません。

代入

変数に式や値を代入するときは : (コロン)を使います。

変数 a に，$100 + 3/21$ を代入して， a を使って計算を続けます.

In [9]:
a: 100 + 3/21;
Out[9]:
\[\tag{${\it \%o}_{9}$}\frac{701}{7}\]
In [10]:
(a - 100) * 7;
Out[10]:
\[\tag{${\it \%o}_{10}$}1\]

変数 eq に式 $x^2 + 3 x + 2$ を代入します。

In [11]:
eq: x^2 + 3*x + 2;
Out[11]:
\[\tag{${\it \%o}_{11}$}x^2+3\,x+2\]

eq を factor 関数で因数分解します。

In [12]:
factor(eq);
Out[12]:
\[\tag{${\it \%o}_{12}$}\left(x+1\right)\,\left(x+2\right)\]

関数の定義

関数の定義には := を使います。$f(x) := x^2$

In [13]:
f(x):= x^2;
Out[13]:
\[\tag{${\it \%o}_{13}$}f\left(x\right):=x^2\]

$f(4) = 4^2 = 16$

In [14]:
f(4);
Out[14]:
\[\tag{${\it \%o}_{14}$}16\]

$f(3\sqrt{A}) = (3\sqrt{A})^2 = 9 A$ です。

In [15]:
f(sqrt(A)*3);
Out[15]:
\[\tag{${\it \%o}_{15}$}9\,A\]

$\frac{d}{dx}(x \cos x)$ を計算します。

In [16]:
diff(x*cos(x), x);
Out[16]:
\[\tag{${\it \%o}_{16}$}\cos x-x\,\sin x\]

以下の例のように f(x):= % のような 仕方で（直前の）計算結果を参照して関数を定義することはできません。

In [17]:
g(x):= %;
Out[17]:
\[\tag{${\it \%o}_{17}$}g\left(x\right):={\it \%}\]
In [18]:
g(x);
Out[18]:
\[\tag{${\it \%o}_{18}$}g\left(x\right):={\it \%}\]

このような場合には define を使います。%o16 は 16 番目の出力結果（今の場合は $\cos(x) − x \sin(x)$ です。）

In [19]:
define(g(x), %o16);
Out[19]:
\[\tag{${\it \%o}_{19}$}g\left(x\right):=\cos x-x\,\sin x\]
In [20]:
integrate(g(x), x);
Out[20]:
\[\tag{${\it \%o}_{20}$}x\,\cos x\]

実行結果の非表示

文末に $ をつけると実行結果の出力を省略します。

In [21]:
eq: x^2 + 3*x + 2$

変数 eq を出力させると... 確かに式 $x^2 +3x+2$ ですね.

In [22]:
eq;
Out[22]:
\[\tag{${\it \%o}_{22}$}x^2+3\,x+2\]

2 次方程式 $x^2 +3x+2 = 0$ を solve を使って解いていますが，結果は出力されません。$ ではなく ; を文末 につけると結果が出力されます。

In [23]:
solve(eq = 0, x)$
In [24]:
solve(eq = 0, x);
Out[24]:
\[\tag{${\it \%o}_{24}$}\left[ x=-2 , x=-1 \right] \]

前の出力結果の参照

直前の出力結果は % と表します。これを参照してさらに計算することができます。また，以前の結果を参照する場合は %o26 のように行番号を指定することもできます。

expand 関数を使って展開します。

In [25]:
expand((x - 2)^4);
Out[25]:
\[\tag{${\it \%o}_{25}$}x^4-8\,x^3+24\,x^2-32\,x+16\]

直前の結果を factor 関数で因数分解します。

In [26]:
factor(%);
Out[26]:
\[\tag{${\it \%o}_{26}$}\left(x-2\right)^4\]

行番号 %o26 の結果を展開します。

In [27]:
expand(%o26);
Out[27]:
\[\tag{${\it \%o}_{27}$}x^4-8\,x^3+24\,x^2-32\,x+16\]

一時的代入

ev 関数を使うことで，一時的に式などに値を代入する事ができます。

変数 c に 2*x を代入します。

In [28]:
c: 2*x;
Out[28]:
\[\tag{${\it \%o}_{28}$}2\,x\]

x=3 を一時的に代入して c の値を評 価します。

In [29]:
ev(c, x=3);
Out[29]:
\[\tag{${\it \%o}_{29}$}6\]

c の定義そのものは変わりません。

In [30]:
c;
Out[30]:
\[\tag{${\it \%o}_{30}$}2\,x\]

リスト成分や右辺の取り出し

方程式の解などは，リスト形式 ([ ] で囲まれた形)で出力します。 リスト成分は [ ] で取 り出すことができます。

関数 f(x) を定義します。

In [31]:
f(x):= x^2 + 3*x + 2;
Out[31]:
\[\tag{${\it \%o}_{31}$}f\left(x\right):=x^2+3\,x+2\]

solve で方程式 f(x) = 0 を解きます。

In [32]:
sol: solve( f(x) = 0, x );
Out[32]:
\[\tag{${\it \%o}_{32}$}\left[ x=-2 , x=-1 \right] \]

リストとして表されている 2 個の解のうち，1 番目を sol[1] として， 2 番目を sol[2] としてそれぞれ取り出します。

In [33]:
sol[1];
sol[2];
Out[33]:
\[\tag{${\it \%o}_{33}$}x=-2\]
Out[33]:
\[\tag{${\it \%o}_{34}$}x=-1\]

rhs は右辺 (right hand side) を取り出す関数です。また，左辺を取り出す関数は lhs (left hand side) です。

x = -2 の右辺を取り出して ans1 に代入します。

二つめの解も同様に ans2 に代入します。

In [34]:
ans1: rhs(sol[1]);
ans2: rhs(sol[2]);
Out[34]:
\[\tag{${\it \%o}_{35}$}-2\]
Out[34]:
\[\tag{${\it \%o}_{36}$}-1\]

関数 f(x) に解を入れると確かに 0 になります。

In [35]:
f(ans1);
Out[35]:
\[\tag{${\it \%o}_{37}$}0\]
In [36]:
f(ans2);
Out[36]:
\[\tag{${\it \%o}_{38}$}0\]

以下は見慣れない書式ですが， ev(f(x), sol[1]) の簡略形です。

In [37]:
f(x), sol[1];
Out[37]:
\[\tag{${\it \%o}_{39}$}0\]

数の計算・基本的な関数

基本的な演算

1 から 10 までの和を求めてみます。

In [38]:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
Out[38]:
\[\tag{${\it \%o}_{40}$}55\]

同様の計算は公式 $\sum_{i = 1}^{n} = n (n + 1)/2$ を 使ってもできます。

In [39]:
n: 10$
n*(n + 1)/2;
Out[39]:
\[\tag{${\it \%o}_{42}$}55\]
In [40]:
kill(n)$
ev(n*(n + 1)/2, n = 10);
Out[40]:
\[\tag{${\it \%o}_{44}$}55\]

以下は，ev(n*(n + 1)/2, n = 10) の簡略形でしたね。

In [41]:
n*(n+1)/2, n = 10;
Out[41]:
\[\tag{${\it \%o}_{45}$}55\]

基本的な四則演算 (+ - * /) 以外によく使われる演算記号を示します。

$2^4$ の計算。累乗は ^ で表します。^ のかわりに ** でもよいようです。

In [42]:
2^4;
Out[42]:
\[\tag{${\it \%o}_{46}$}16\]
In [43]:
2**4;
Out[43]:
\[\tag{${\it \%o}_{47}$}16\]

4 の階乗の計算をします. 4! = 4*3*2*1 = 24 です。

In [44]:
4!;
Out[44]:
\[\tag{${\it \%o}_{48}$}24\]

!! は，一つおきの階乗の計算をします。5!! = 5*3*1 です。

In [45]:
5!!;
Out[45]:
\[\tag{${\it \%o}_{49}$}15\]

練習

(練習) 3, 2, 1 でつくる最大の数

数字の 3 と 2 と 1 を 1 個ずつ使った演算でつくることができる最大の整数は?

ヒント:

(1 + 2) × 3 = 9 じゃ全然だめ。そのまま並べると 321 ですが，累乗を使うともっと大きい数をつくることができます。 $21^3$ とか，$31^2$ とか，$2^{31}$ とか...

基本的な定数

Maxima の基本的な定数を示します。
円周率 $\pi$ 無限大 $\infty$ 自然対数の底 $e$ 虚数単位 $i$
%pi inf %e %i

無理数 $e$，$\pi$ と虚数単位 $i$ と整数 $−1$ の間のすてきな関係，オイラーの等式 $$e^{i\pi} = -1$$

In [46]:
%e^(%i * %pi);
Out[46]:
\[\tag{${\it \%o}_{50}$}-1\]

浮動小数点で近似値を表示するには float や bfloat を使います。

In [47]:
%pi; 
float(%pi);
bfloat(%pi);
Out[47]:
\[\tag{${\it \%o}_{51}$}\pi\]
Out[47]:
\[\tag{${\it \%o}_{52}$}3.141592653589793\]
Out[47]:
\[\tag{${\it \%o}_{53}$}3.141592653589793_B \times 10^{0}\]

float は 16 桁の値を返します.それ以上の桁数を見たいときには，bfloat を使います。bfloat の表示桁数は fpprec で指定します。

有効数字 32 桁で円周率 $\pi$ を表示す る例です。

In [48]:
fpprec: 32$ bfloat(%pi);
Out[48]:
\[\tag{${\it \%o}_{55}$}3.1415926535897932384626433832795_B \times 10^{0}\]

基本的な関数

基本的な関数は以下のように表記されます。
平方根 指数関数 自然対数 絶対値 三角関数 逆関数 双曲線関数
sqrt exp log abs sin cos tan asin acos atan sinh cosh tanh

うっかり $\sqrt{x^2} = x$ としないように。 $\sqrt{x^2} = |x|$ です。

In [49]:
sqrt(x^2);
Out[49]:
\[\tag{${\it \%o}_{56}$}\left| x\right| \]

ピタゴラスの定理をみたす整数の例。 $\sqrt{3^2 + 4^2} = 5$ ですね。

In [50]:
sqrt(3^2 + 4^2);
Out[50]:
\[\tag{${\it \%o}_{57}$}5\]

$\exp(1) = e$ のこと。

$e^{\log x}$ や $\log(e^2)$ の計算。

In [51]:
exp(log(x));
log(%e^2);
Out[51]:
\[\tag{${\it \%o}_{58}$}x\]
Out[51]:
\[\tag{${\it \%o}_{59}$}2\]

練習

（練習）ピタゴラス数

$a^2 + b^2 = c^2$ を満たす正の整数の組をピタゴラス数といいます。ピタゴラス数は二つの任意の正の整数 $m, n$ から以下のように何組でもつくることができます。

$$a=|m^2 −n^2|, \ b=2mn, \ c= \sqrt{a^2 +b^2} $$

このとき，$c$ は必ず整数になることを示しなさい。

試しにやってみます。

In [52]:
kill(m, n)$ /* m, n を初期化 */
a: abs(m^2 - n^2);
b: 2 * m * n;
c: sqrt(a^2 + b^2);
Out[52]:
\[\tag{${\it \%o}_{61}$}\left| n^2-m^2\right| \]
Out[52]:
\[\tag{${\it \%o}_{62}$}2\,m\,n\]
Out[52]:
\[\tag{${\it \%o}_{63}$}\sqrt{\left(n^2-m^2\right)^2+4\,m^2\,n^2}\]

直接証明することも簡単ですが，疑似乱数を使って，ちょっとした数値実験をしてみます。

random(100) は 0 から 99 までの整 数疑似乱数をつくる関数です。

In [53]:
[a, b, c], m = random(100), n = random(100);
[a, b, c], m = random(100), n = random(100);
[a, b, c], m = random(100), n = random(100);
Out[53]:
\[\tag{${\it \%o}_{64}$}\left[ 140 , 48 , 148 \right] \]
Out[53]:
\[\tag{${\it \%o}_{65}$}\left[ 6069 , 5780 , 8381 \right] \]
Out[53]:
\[\tag{${\it \%o}_{66}$}\left[ 8265 , 728 , 8297 \right] \]

$c = \sqrt{a^2 + b^2}$ は確かに整数になっています。証明も簡単ですね。

練習

（練習）星の明るさと等級

夜空に見える星の明るさ $L$ は等級 $m$ で表され，以下のような関係があります。

$m = −2.5 \log_{10} L + \mbox{const.}\quad$ ($\mbox{const.}$ は定数のこと)

1 等星と 6 等星では，どちらが何倍明るいですか?

load(log10)$ とすると，常用対数 $\log_{10}$ が使えます.

$$\log_{10} 1000 = \log_{10} 10^3 = 3$$

ですね.

In [54]:
load(log10)$
log10(1000);
Out[54]:
\[\tag{${\it \%o}_{68}$}3\]

三角関数の値・引数の単位

三角関数の値を数値で求めたいときには，以下のようにします。

$\displaystyle \sin\frac{\pi}{3}$ の値は...

In [55]:
sin(%pi/3);
Out[55]:
\[\tag{${\it \%o}_{69}$}\frac{\sqrt{3}}{2}\]

float 関数を使って，直前の結果を 浮動小数点表示します。

In [56]:
float(%);
Out[56]:
\[\tag{${\it \%o}_{70}$}0.8660254037844386\]

変数 pi に浮動小数点表示の $\pi$ の値を代入します。 浮動小数点表示で数値を入れると， sin も浮動小数点表示で答えを返します。

In [57]:
pi: float(%pi);
sin(pi/3);
Out[57]:
\[\tag{${\it \%o}_{71}$}3.141592653589793\]
Out[57]:
\[\tag{${\it \%o}_{72}$}0.8660254037844386\]

三角関数の引数はラジアンです。度を使って求めたいときは以下のようにします。

度をラジアンに変換する関数 degrad を定義します。

degrad(60) を引数にして sin の値を求めます。

In [58]:
degrad(x):= x/180*%pi$
sin(degrad(60));
Out[58]:
\[\tag{${\it \%o}_{74}$}\frac{\sqrt{3}}{2}\]

練習

（練習）屋根勾配

家の屋根の勾配は角度ではなく，伝統的に 3 寸勾配，4 寸勾配のように水平方向に 1 尺(10 寸)に対して垂直方向に何寸立ち上がるかで示します。

図のログハウスの屋根は 8 寸勾配です。 傾斜角度にすると何度ですか?

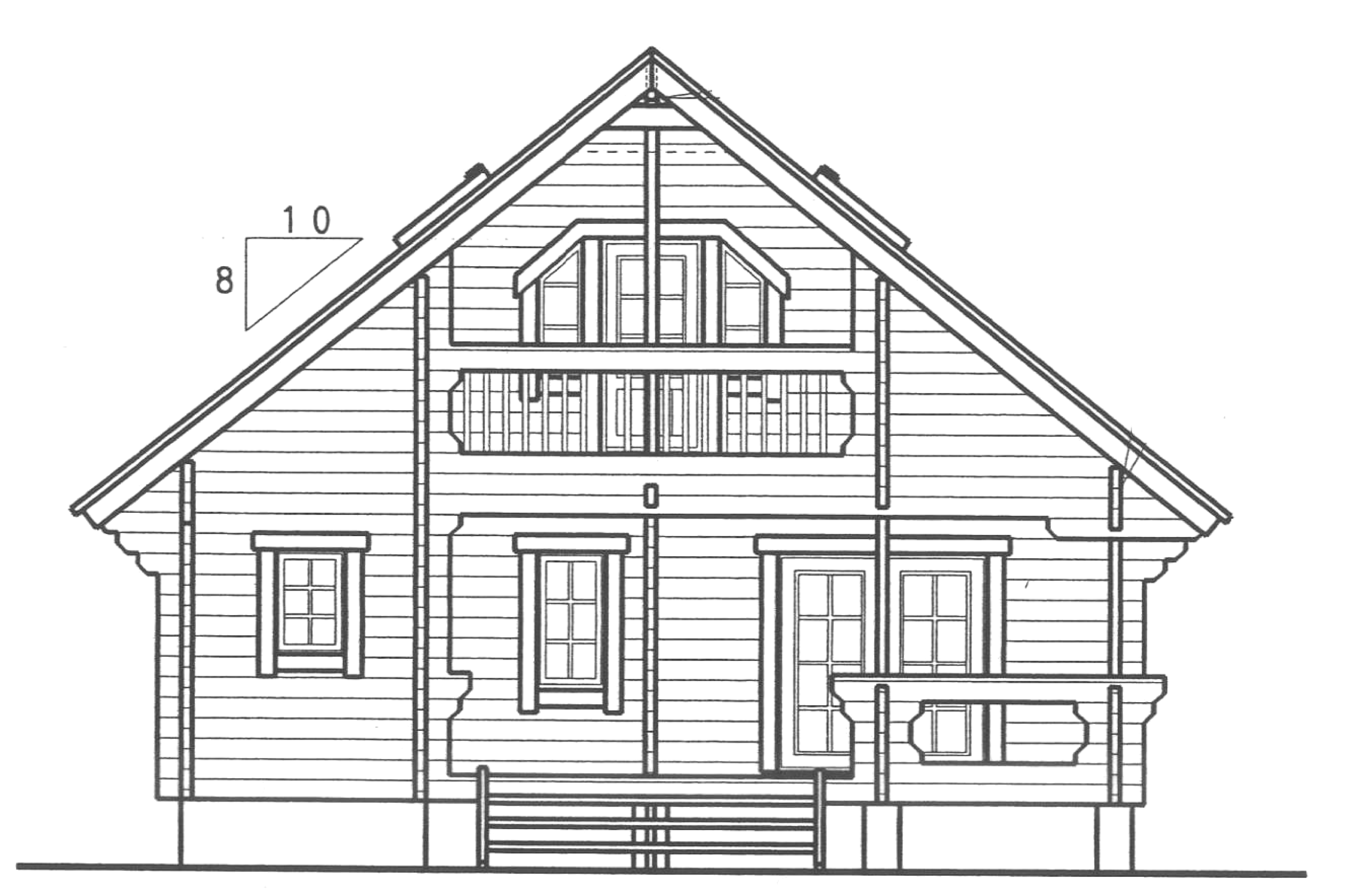
以下に各寸勾配の角度の表があります。10 寸勾配まで表 を完成させましょう。

勾配 1寸勾配 2寸勾配 3寸勾配 ...
atan(0.1) atan(0.2) atan(0.3) ...
rad 0.0997 0.1974 0.2915 ...
度 5.7106° 11.3099° 16.6992° ...

数列の和

数列の和を計算する関数 sum の書式は，sum(一般項 a_i，i，はじめの i，最後の i) です。

$\displaystyle \sum_{i=1}^{100} i^2$ の計算をします。

In [59]:
sum(i^2, i, 1, 10);
Out[59]:
\[\tag{${\it \%o}_{75}$}385\]

一般の $n$ までの和は $\displaystyle \sum_{i=1}^{n} i^2$ ですが...

In [60]:
kill(n)$
sum(i^2, i, 1, n);
Out[60]:
\[\tag{${\it \%o}_{77}$}\sum_{i=1}^{n}{i^2}\]

sum 関数は答えを出してくれません。nusum は $n$ までの和を知っています。

In [61]:
nusum(i^2, i, 1, n);
Out[61]:
\[\tag{${\it \%o}_{78}$}\frac{n\,\left(n+1\right)\,\left(2\,n+1\right)}{6}\]

練習

（練習）数列の和

  1. 初項が $a_1$，公差 $d$ の等差数列の第 $1$ 項から第 $n$ 項までの和を求めよ。
  2. 初項が $b_1$，公比が $r$ の等比数列について，第 $n$ 項までの和を求めよ。
  3. 初項が $3$，公比が $2$ の等比数列について，第 10 項までの和を求めよ。
  4. 無限等比数列の和 $\displaystyle \sum_{i=1}^{\infty} b_1\,r^{i-1}$ を求めよ。ただし，$0 < r < 1$。
In [62]:
/* 1. のヒント */
a(a1, d, i):= a1 + d*(i-1);
nusum(a(a1, d, i), i, 1, n)$
Out[62]:
\[\tag{${\it \%o}_{79}$}a\left(a_{1} , d , i\right):=a_{1}+d\,\left(i-1\right)\]
In [63]:
/* 2. と 3. のヒント */
kill(b, b1, r, i)$

b(b1, r, i):= b1 * r^(i-1);
nusum(b(b1, r, i), i, 1, n)$
%, b1=3, r=2, n=10$
Out[63]:
\[\tag{${\it \%o}_{82}$}b\left(b_{1} , r , i\right):=b_{1}\,r^{i-1}\]
In [64]:
/* 4. のヒント */
/* r の範囲を宣言して... */
assume( 0 < r, r < 1);
nusum(b(b1, r, i), i, 1, n)$
limit(%, n, inf)$
Out[64]:
\[\tag{${\it \%o}_{85}$}\left[ r>0 , r<1 \right] \]

関数のテイラー展開

$\sin x$ を$x = 0$ のまわりで $x^5$ までテイラー展開する例。

In [65]:
taylor(sin(x), x, 0, 5);
Out[65]:
\[\tag{${\it \%o}_{88}$}\frac{x^5}{120}-\frac{x^3}{6}+x\]

$e^{ix}$（$i$ は虚数単位）のテイラー展開。

In [66]:
ty: taylor(exp(%i*x), x, 0, 5);
Out[66]:
\[\tag{${\it \%o}_{89}$}\frac{i\,x^5}{120}+\frac{x^4}{24}-\frac{i\,x^3}{6}-\frac{x^2}{2}+i\,x+1\]

上記の虚部を imagpart，実部を realpart でとります。

In [67]:
imagpart(ty);
Out[67]:
\[\tag{${\it \%o}_{90}$}\frac{x^5}{120}-\frac{x^3}{6}+x\]
In [68]:
realpart(ty);
Out[68]:
\[\tag{${\it \%o}_{91}$}\frac{x^4}{24}-\frac{x^2}{2}+1\]

$\cos x, \tan x, \log (1 + x)$ 等のテイラー展開もやってみましょう。

In [69]:
taylor(log(1 + x), x, 0, 5);
Out[69]:
\[\tag{${\it \%o}_{92}$}\frac{x^5}{5}-\frac{x^4}{4}+\frac{x^3}{3}-\frac{x^2}{2}+x\]

式の整理・簡単化

Maxima では，多項式やいろいろな関数を含んだ式の変形や整理・簡単化が可能です。

展開・因数分解・簡単化

$(x + 1)^2$ を展開します。

In [70]:
(x + 1)^2;
expand(%);
Out[70]:
\[\tag{${\it \%o}_{93}$}\left(x+1\right)^2\]
Out[70]:
\[\tag{${\it \%o}_{94}$}x^2+2\,x+1\]

$x^3 - 1$ を因数分解します。

In [71]:
factor(x^3 - 1);
Out[71]:
\[\tag{${\it \%o}_{95}$}\left(x-1\right)\,\left(x^2+x+1\right)\]

$\displaystyle \frac{3}{x^3 -1}$ を部分分数に展開する例。

In [72]:
partfrac(3/(x^3 - 1), x);
Out[72]:
\[\tag{${\it \%o}_{96}$}\frac{-x-2}{x^2+x+1}+\frac{1}{x-1}\]

ratsimp を使って，上式を「簡単化」します。

In [73]:
ratsimp(%);
Out[73]:
\[\tag{${\it \%o}_{97}$}\frac{3}{x^3-1}\]

三角関数を含む式の簡単化

三角関数や双曲線関数を含む式の簡単化には，trigsimp 関数などを使います。

$\cos^2 x - \sin^2 x$ を「簡単化」します。

In [74]:
trigsimp(cos(x)^2 - sin(x)^2);
Out[74]:
\[\tag{${\it \%o}_{98}$}2\,\cos ^2x-1\]

trigreduce は三角関数同士の積をなるべく減らして「簡単化」します。

In [75]:
trigreduce(cos(x)^2 - sin(x)^2);
Out[75]:
\[\tag{${\it \%o}_{99}$}\frac{\cos \left(2\,x\right)+1}{2}+\frac{\cos \left(2\,x\right)}{2}-\frac{1}{2}\]

通分すればもっと簡単になりますね。このへんが Maxima のつれないところです。

In [76]:
trigsimp(%);
Out[76]:
\[\tag{${\it \%o}_{100}$}\cos \left(2\,x\right)\]

trigexpand 関数は加法定理や倍角の公式を使って「展開」します。

In [77]:
trigexpand(cos(3*x));
trigsimp(%);
Out[77]:
\[\tag{${\it \%o}_{101}$}\cos ^3x-3\,\cos x\,\sin ^2x\]
Out[77]:
\[\tag{${\it \%o}_{102}$}4\,\cos ^3x-3\,\cos x\]

練習

(練習)加法定理・三倍角の公式

  1. 三角関数及び双曲線関数の加法定理を確認しなさい。
  2. $\sin 3x$ を $\sin x$ だけを使って表しなさい。
  3. $\tan 3x$ を $\tan x$ だけを使って表しなさい.
In [78]:
/* 1. のヒント */
/* trigexpand で展開します。*/
trigexpand(sin(x + y))$
trigexpand(cos(x + y))$
trigexpand(tan(x + y))$
trigexpand(sinh(x + y))$
trigexpand(cosh(x + y))$
trigexpand(tanh(x + y))$
In [79]:
/* 2. や 3. のヒント */
trigexpand(sin(3*x));
trigsimp(%);
Out[79]:
\[\tag{${\it \%o}_{109}$}3\,\cos ^2x\,\sin x-\sin ^3x\]
Out[79]:
\[\tag{${\it \%o}_{110}$}\left(4\,\cos ^2x-1\right)\,\sin x\]

$\cos(x)^2$ を $1-\sin(x)^2$ で置き換える例です。

In [80]:
ratsubst(1-sin(x)^2, cos(x)^2, %)$

微分・積分・数値積分

微分・積分を行う関数の表記を以下に示します。

操作 表記例
微分 diff(f(x), x)
n 階微分 diff(f(x), x, n)
不定積分 integrate(f(x), x)
定積分 integrate(f(x), x, a, b)
数値積分 romberg(f(x), x, a, b)

微分・積分

$x^3 +5x+2$ を $x$ で微分します。

In [81]:
diff(x^3 + 5*x + 2, x);
Out[81]:
\[\tag{${\it \%o}_{112}$}3\,x^2+5\]

$x^3 +5x+2$ を $x$ で 2 階微分します。

In [82]:
diff(x^3 + 5*x + 2, x, 2);
Out[82]:
\[\tag{${\it \%o}_{113}$}6\,x\]

$x^2 \cos x + 2 x \sin x$ を $x$ で積分しま す。

In [83]:
integrate(x^2*cos(x) + 2*x*sin(x), x);
Out[83]:
\[\tag{${\it \%o}_{114}$}2\,\left(\sin x-x\,\cos x\right)+\left(x^2-2\right)\,\sin x+2\,x\,\cos x\]

もう少し簡単になりそうですね。このへんが Maxima のつれないところです。

In [84]:
trigsimp(%);
Out[84]:
\[\tag{${\it \%o}_{115}$}x^2\,\sin x\]

定積分の例：$\displaystyle \int_0^{\pi/2} \sin x \, dx = 1$

以下の例では ' から始めると，その部分の計算を実行せずに形を整えて表示だけしてくれるところを示しています。

In [85]:
'integrate(sin(x), x, 0, %pi/2) = 
 integrate(sin(x), x, 0, %pi/2);
Out[85]:
\[\tag{${\it \%o}_{116}$}\int_{0}^{\frac{\pi}{2}}{\sin x\;dx}=1\]

有名なガウス積分。不定積分はできないのに，無限区間の定積分だけはできる！という例。

In [86]:
'integrate(exp(-x^2), x, -inf, inf) = 
 integrate(exp(-x^2), x, -inf, inf);
Out[86]:
\[\tag{${\it \%o}_{117}$}\int_{-\infty }^{\infty }{e^ {- x^2 }\;dx}=\sqrt{\pi}\]

練習

（練習）関数の傾き

$\displaystyle y = \frac{2x - 1}{x+1}$ が $x \neq -1$ で増加関数であることを示しなさい。

練習

（練習）積分

以下の積分をしなさい。

$$1.\ \int e^x \sin x \ dx \qquad 2. \ \int \frac{x^2 - 2 x - 2}{x^3 -1}\ dx$$

数値積分

解析的に積分できない場合は，数値積分によって近似値を求めることができます。

$\displaystyle \int_0^{\pi} \sin(\sin x)\ dx$ の計算をします。

In [87]:
integrate(sin(sin(x)), x, 0, %pi);
Out[87]:
\[\tag{${\it \%o}_{118}$}\int_{0}^{\pi}{\sin \sin x\;dx}\]

解析的に解けないと，そのままで返します。

romberg 関数を使うと，数値的に積分した結果を表示します。

In [88]:
r1: romberg(sin(sin(x)), x, 0, %pi);
Out[88]:
\[\tag{${\it \%o}_{119}$}1.786487487137068\]

数値積分 romberg の精度は，大域変数 rombergtol で決まります。

rombergtol の値を小さくすることで精度をあげることができます。

デフォルトの rombergtol の値は...

In [89]:
rombergtol;
Out[89]:
\[\tag{${\it \%o}_{120}$}1.0 \times 10^{-4}\]

rombergtol を $10^{-12}$ にしてもう一度同じ数値積分を行うと...

In [90]:
rombergtol: 1.e-12$
r2: romberg(sin(sin(x)), x, 0, %pi);
Out[90]:
\[\tag{${\it \%o}_{122}$}1.786487481950052\]
In [91]:
r1 - r2;
Out[91]:
\[\tag{${\it \%o}_{123}$}5.187015705843123 \times 10^{-9}\]

方程式

多項式方程式・連立方程式

Maxima は，式の計算だけでなく，代数方程式を解くことができます.例を以下に示します。

$x^2 +2x−2 = 0$ を $x$ について解き ます.

In [92]:
solve(x^2 + 2*x - 2 = 0, x);
Out[92]:
\[\tag{${\it \%o}_{124}$}\left[ x=-\sqrt{3}-1 , x=\sqrt{3}-1 \right] \]

連立方程式 $x^2 + y^2 = 5, \ x + y = 1$ を $x, y$ について解きます。

In [93]:
solve([x^2+y^2=5, x+y=1], [x, y]);
Out[93]:
\[\tag{${\it \%o}_{125}$}\left[ \left[ x=-1 , y=2 \right] , \left[ x=2 , y=-1 \right] \right] \]

solve の代わりに algsys も使えます。

In [94]:
algsys([x^2+y^2=5, x+y=1], [x, y]);
Out[94]:
\[\tag{${\it \%o}_{126}$}\left[ \left[ x=-1 , y=2 \right] , \left[ x=2 , y=-1 \right] \right] \]

3 次方程式 $x^3 = 8$ を解きます。

In [95]:
solve(x^3 = 8, x);
Out[95]:
\[\tag{${\it \%o}_{127}$}\left[ x=\sqrt{3}\,i-1 , x=-\sqrt{3}\,i-1 , x=2 \right] \]

確認のため，上記の1番目の答えを3乗して簡単化すると...

In [96]:
rhs(%[1])^3, ratsimp;
Out[96]:
\[\tag{${\it \%o}_{128}$}8\]

実数解のみを求める場合は， realroots を使います。

In [97]:
realroots(x^3 = 8);
Out[97]:
\[\tag{${\it \%o}_{129}$}\left[ x=2 \right] \]

練習

（練習）鶴と亀と蟻

鶴と亀と蟻，個体数の合計は 10。足の数は全部で 34 本。蟻は亀より 1 匹少ない。鶴，亀，蟻，それぞれ何羽・何匹?

鶴と亀と蟻の個体数をそれぞれ $x, y, z$ として連立方程式をたてて solve します。蟻の足は何本かわかりますよね?

かつて線形代数の授業でこの問題を出したとき，真っ先に出た質問が「先生，蟻の足は何本ですか？」でした... orz

方程式の数値解

1 変数多項式方程式の数値解を求める関数として， allroots や find_root があります。

$f(x) := x^3 + 8x - 3$ と定義します。

In [98]:
f(x):= x^3 + 8*x - 3;
Out[98]:
\[\tag{${\it \%o}_{130}$}f\left(x\right):=x^3+8\,x-3\]

allroots を使って，$f(x) = 0$ の全数値解を求めます。

In [99]:
asol: allroots(f(x) = 0);
Out[99]:
\[\tag{${\it \%o}_{131}$}\left[ x=0.3687331875693762 , x=2.846396515370145\,i-0.1843665937846881 , x=-2.846396515370145\,i-0.1843665937846881 \right] \]

realroots を使って $f(x) = 0$ の実 数解を求めます。

In [100]:
rsol: realroots(f(x) = 0);
float(%);
Out[100]:
\[\tag{${\it \%o}_{132}$}\left[ x=\frac{12372633}{33554432} \right] \]
Out[100]:
\[\tag{${\it \%o}_{133}$}\left[ x=0.3687331974506378 \right] \]

allroots で求めた結果と少し違いますね。

精度を指定して再計算してみます。

In [101]:
realroots(f(x) = 0, 1e-16)$
float(%);
Out[101]:
\[\tag{${\it \%o}_{135}$}\left[ x=0.3687331875693762 \right] \]

多項式方程式でない場合には find_root 関数を使って，範囲を指定して解を探します。

関数 $g(x):= (x − 1)\,e^x$ の定義。

$g(x):= (x − 1)\,e^x = 1$ の解は solve などでは求めることができません。

In [102]:
g(x):= (x - 1)*exp(x);
solve(g(x) = 1, x);
Out[102]:
\[\tag{${\it \%o}_{136}$}g\left(x\right):=\left(x-1\right)\,\exp x\]
Out[102]:
\[\tag{${\it \%o}_{137}$}\left[ x=e^ {- x }\,\left(e^{x}+1\right) \right] \]

find_root を使って $0 \leq x \leq 2$ の 範囲で解を探してみます。

出た答えを代入して確かめると...

In [103]:
find_root(g(x) = 1, x, 0, 2);
g(%);
Out[103]:
\[\tag{${\it \%o}_{138}$}1.278464542761074\]
Out[103]:
\[\tag{${\it \%o}_{139}$}1.0\]

練習

（練習）関数の極大値

次の関数が極大値をとる $x$ の値およびその極大値を求めよ。

$$ 1. \ \ f(x) = \frac{x^3}{e^x - 1}, \qquad 2. \ \ g(x) = \frac{x^5}{e^x -1}$$
In [104]:
/* 1. のヒント */
/* f(x) を定義して，それを微分して... */
f(x):= x^3/(exp(x) - 1);
diff(f(x), x);
define(df(x), %);

/* 導関数が 0 になる x を数値的に求める */
find_root(df(x) = 0, x, 1, 5)$

/* 極値は... */
f(%)$
Out[104]:
\[\tag{${\it \%o}_{140}$}f\left(x\right):=\frac{x^3}{\exp x-1}\]
Out[104]:
\[\tag{${\it \%o}_{141}$}\frac{3\,x^2}{e^{x}-1}-\frac{x^3\,e^{x}}{\left(e^{x}-1\right)^2}\]
Out[104]:
\[\tag{${\it \%o}_{142}$}{\it df}\left(x\right):=\frac{3\,x^2}{e^{x}-1}-\frac{x^3\,e^{x}}{\left(e^{x}-1\right)^2}\]

常微分方程式: ode2

Maxima は 1 階および 2 階の常微分方程式も扱うことができます。 まず ode2 関数を使って 解く例を示します。

1 階常微分方程式と初期条件

微分方程式を記述する際は diff の 前の ’ に注意。

ode2 で $\displaystyle \frac{dy}{dt} = a y$ を解きます。

In [105]:
kill(a, t, y)$ /* 念のため，これから使う変数を初期化。 */

ode2('diff(y, t) = a* y, y, t);
Out[105]:
\[\tag{${\it \%o}_{146}$}y={\it \%c}\,e^{a\,t}\]

%c は積分定数です。

1 階常微分方程式の初期条件には ic1 を使い，例えば初期条件を $t = 0$ で $y = 1$ とすると積分定数 %c の値が決まります。

In [106]:
ic1(%, t = 0, y = 1);
Out[106]:
\[\tag{${\it \%o}_{147}$}y=e^{a\,t}\]

2 階常微分方程式と初期条件

2階常微分方程式 $\displaystyle \frac{d^2 x}{dt^2} + K x = 0$ を解く例です。

ここでは単振動の運動方程式を想定しているので $K > 0$です。あとで聞かれないように最初に仮定しておきます。

In [107]:
assume( K > 0);
ode2('diff(x, t, 2) + K*x = 0, x, t);
Out[107]:
\[\tag{${\it \%o}_{148}$}\left[ K>0 \right] \]
Out[107]:
\[\tag{${\it \%o}_{149}$}x={\it \%k}_{1}\,\sin \left(\sqrt{K}\,t\right)+{\it \%k}_{2}\,\cos \left(\sqrt{K}\,t\right)\]

%k1，%k2 は積分定数です。

2 階常微分方程式の初期条件は ic2 で設定します。 初期条件を $t = 0$ で $x=x_0, v=v_0$ とすると %k1，%k2 が決まります。

In [108]:
ic2(%, t = 0, x = x[0], 'diff(x, t) = v[0]);
Out[108]:
\[\tag{${\it \%o}_{150}$}x=\frac{v_{0}\,\sin \left(\sqrt{K}\,t\right)}{\sqrt{K}}+x_{0}\,\cos \left(\sqrt{K}\,t\right)\]

細かいことですが，x[0] のようにすると Maxima は下付きの添字 $x_0$ として表示します。

常微分方程式: desolve

常微分方程式を解く関数としては desolve もあります。 ode2 と書式が若干違います。

また，初期条件は atvalue 関数で先に設定しておきます。

2 階の常微分方程式 $\displaystyle \frac{d^2 x}{dt^2} + K x = 0$ を解く例を以下に示します。

In [109]:
atvalue(x(t), t = 0, x[0]);
atvalue('diff(x(t), t), t = 0, v[0]);
Out[109]:
\[\tag{${\it \%o}_{151}$}x_{0}\]
Out[109]:
\[\tag{${\it \%o}_{152}$}v_{0}\]
In [110]:
desolve('diff(x(t), t, 2) + K*x(t) = 0, x(t));
Out[110]:
\[\tag{${\it \%o}_{153}$}x\left(t\right)=\frac{v_{0}\,\sin \left(\sqrt{K}\,t\right)}{\sqrt{K}}+x_{0}\,\cos \left(\sqrt{K}\,t\right)\]

ちなみに，$K \rightarrow 0$ の極限で，この解がどうなるかというと...

In [111]:
limit(%, K, 0);
Out[111]:
\[\tag{${\it \%o}_{154}$}x\left(t\right)=v_{0}\,t+x_{0}\]

最初から $K = 0$ とした微分方程式 $\displaystyle \frac{d^2 x}{dt^2} = 0$ を解いても...

In [112]:
desolve('diff(x(t), t, 2) = 0, x(t));
Out[112]:
\[\tag{${\it \%o}_{155}$}x\left(t\right)=v_{0}\,t+x_{0}\]

練習

（練習）重力場中の投げ上げ運動

  1. 高さ $0$ から初速度 $v_0$ で鉛直上方に投げ上げた物体の時刻 $t$ における高さ $y$ を求めなさい。運動方程式は， $$ \frac{d^2 y}{dt^2} = -g$$
  2. 速度に比例する空気抵抗がある場合，運動方程式は以下のようになる。 $$ \frac{d^2 y}{dt^2} = -g - \beta \frac{dy}{dt}$$ このとき，高さ $0$ から初速度 $v_0$ で鉛直上方に投げ上げた物体の時刻 $t$ における高さ $y$ を 求めなさい。
  3. 前問 2. で求めた解が $\beta \rightarrow 0$ のとき，前問 1. の答えに一致することを示しなさい。

ベクトルと行列

3 次元ベクトルの表記

3 次元ベクトル $\boldsymbol{a} = (a_x,a_y,a_z)$ の表記例。

In [113]:
a: [a[x], a[y], a[z]];
Out[113]:
\[\tag{${\it \%o}_{156}$}\left[ a_{x} , a_{y} , a_{z} \right] \]

$\boldsymbol{a}$ の $x$ 成分（第 1 成分）を取り出すには...

In [114]:
a[1];
Out[114]:
\[\tag{${\it \%o}_{157}$}a_{x}\]

ベクトル $\boldsymbol{b}$ も同様に定義。

In [115]:
b: [b[x], b[y], b[z]];
Out[115]:
\[\tag{${\it \%o}_{158}$}\left[ b_{x} , b_{y} , b_{z} \right] \]

内積

ベクトルの内積 $\boldsymbol{a} \cdot \boldsymbol{b}$ には . (ドット)を使います。

In [116]:
a.b;
Out[116]:
\[\tag{${\it \%o}_{159}$}a_{z}\,b_{z}+a_{y}\,b_{y}+a_{x}\,b_{x}\]

内積を利用して，ベクトルの大きさを返す関数 norm を定義します。

In [117]:
norm(v):= sqrt(v.v);
norm(a);
Out[117]:
\[\tag{${\it \%o}_{160}$}{\it norm}\left(v\right):=\sqrt{v\cdot v}\]
Out[117]:
\[\tag{${\it \%o}_{161}$}\sqrt{a_{z}^2+a_{y}^2+a_{x}^2}\]

外積

ベクトルの外積 $\boldsymbol{a} \times \boldsymbol{b}$ を返す関数 cross を定義します。

In [118]:
cross(u, v):=
           [u[2]*v[3] - u[3]*v[2],
            u[3]*v[1] - u[1]*v[3],
            u[1]*v[2] - u[2]*v[1]]$

成分ごとに見てみます。

In [119]:
cross(a, b)[1];
cross(a, b)[2];
cross(a, b)[3];
Out[119]:
\[\tag{${\it \%o}_{163}$}a_{y}\,b_{z}-b_{y}\,a_{z}\]
Out[119]:
\[\tag{${\it \%o}_{164}$}b_{x}\,a_{z}-a_{x}\,b_{z}\]
Out[119]:
\[\tag{${\it \%o}_{165}$}a_{x}\,b_{y}-b_{x}\,a_{y}\]

練習

（練習）ベクトルの内積，外積

$\displaystyle \boldsymbol{a} = \left(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, \sqrt{3}\right), \boldsymbol{b} = \left(-1, 1, -\sqrt{2}\right)$ について，以下の量を計算しなさい。

$$1.\ \ |\boldsymbol{a}|, \quad 2.\ \ |\boldsymbol{b}|, \quad 3. \ \ \boldsymbol{a}\cdot\boldsymbol{b}, \quad 4. \ \ \boldsymbol{a}\times\boldsymbol{b}, \quad 5. \ \ \cos\theta, \quad 6. \ \ \sin\theta$$

ここで $\theta$ は2つのベクトルのなす角。

練習

（練習）ベクトルの 3 重積

  1. スカラー3重積の以下の性質を確かめなさい。 $$\boldsymbol{a}\cdot (\boldsymbol{b}\times\boldsymbol{c}) = \boldsymbol{b}\cdot (\boldsymbol{c}\times\boldsymbol{a}) = \boldsymbol{c}\cdot (\boldsymbol{a}\times\boldsymbol{b}) $$
  2. ベクトル3重積の以下の性質を確かめなさい。 $$\boldsymbol{a}\times (\boldsymbol{b}\times\boldsymbol{c}) = (\boldsymbol{a}\cdot\boldsymbol{c})\,\boldsymbol{b} - (\boldsymbol{a}\cdot\boldsymbol{b})\,\boldsymbol{c} $$
In [120]:
/* 1. のヒント */
kill(c)$

c: [c[x], c[y], c[z]];
a.cross(b, c) - b.cross(c, a)$
expand(%)$
Out[120]:
\[\tag{${\it \%o}_{167}$}\left[ c_{x} , c_{y} , c_{z} \right] \]

行列の簡単な演算

変数を別に再利用する際には，以前の定義を消しておきます。

In [121]:
kill(a, b, c, d)$

2 行 2 列の行列 A の定義。

In [122]:
A: matrix([a, b], [c, d]);
Out[122]:
\[\tag{${\it \%o}_{171}$}\begin{pmatrix}a & b \\ c & d \\ \end{pmatrix}\]

transpose は転置行列。

In [123]:
transpose(A);
Out[123]:
\[\tag{${\it \%o}_{172}$}\begin{pmatrix}a & c \\ b & d \\ \end{pmatrix}\]

determinant は行列式。

In [124]:
determinant(A);
Out[124]:
\[\tag{${\it \%o}_{173}$}a\,d-b\,c\]

逆行列は A^^-1 のように書きます。

In [125]:
A^^-1;
Out[125]:
\[\tag{${\it \%o}_{174}$}\begin{pmatrix}\frac{d}{a\,d-b\,c} & -\frac{b}{a\,d-b\,c} \\ -\frac{c}{a\,d-b\,c} & \frac{a}{a\,d-b\,c} \\ \end{pmatrix}\]

$A^{-1}\, A$ が単位行列になることを確かめます。 行列の積も . (ドット)で 表します。

In [126]:
A^^-1 . A, ratsimp;
Out[126]:
\[\tag{${\it \%o}_{175}$}\begin{pmatrix}1 & 0 \\ 0 & 1 \\ \end{pmatrix}\]

回転行列 O の定義。

In [127]:
O: matrix([cos(x), -sin(x), 0],
          [sin(x),  cos(x), 0],
          [0,      0,       1]);
Out[127]:
\[\tag{${\it \%o}_{176}$}\begin{pmatrix}\cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\]

直交行列とは，転置行列が逆行列になっている行列のこと。この回転を表す行列 O が直交行列であることを示してみます。

In [128]:
transpose(O) - O^^-1;
Out[128]:
\[\tag{${\it \%o}_{177}$}\begin{pmatrix}\cos x-\frac{\cos x}{\sin ^2x+\cos ^2x} & \sin x-\frac{\sin x}{\sin ^2x+\cos ^2x} & 0 \\ \frac{\sin x}{\sin ^2x+\cos ^2x}-\sin x & \cos x-\frac{\cos x}{\sin ^2x+\cos ^2x} & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}\]

うーん，この辺が Maxima のつれないところです。

In [129]:
transpose(O) - O^^-1, trigreduce;
Out[129]:
\[\tag{${\it \%o}_{178}$}\begin{pmatrix}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}\]

以下のようにしても，直交行列であることが示せます。

In [130]:
O. transpose(O);
Out[130]:
\[\tag{${\it \%o}_{179}$}\begin{pmatrix}\sin ^2x+\cos ^2x & 0 & 0 \\ 0 & \sin ^2x+\cos ^2x & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\]
In [131]:
trigsimp(%);
Out[131]:
\[\tag{${\it \%o}_{180}$}\begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\]

3 次元ベクトル $\boldsymbol{r}$ を，3 行 1 列の行列として定義します。このように成分を縦に並べたものを列ベクトルと言うんでしたね。

In [132]:
r: matrix([x], [y], [z]);
Out[132]:
\[\tag{${\it \%o}_{181}$}\begin{pmatrix}x \\ y \\ z \\ \end{pmatrix}\]

3 次元ベクトルの直交変換の例。

In [133]:
O . r;
Out[133]:
\[\tag{${\it \%o}_{182}$}\begin{pmatrix}x\,\cos x-\sin x\,y \\ \cos x\,y+x\,\sin x \\ z \\ \end{pmatrix}\]

練習

（練習）直交変換されたベクトルの大きさ

$\boldsymbol{r}' \equiv O \,\boldsymbol{r}$ の大きさは $\boldsymbol{r}$ の大きさと同じであることを示しなさい。

In [134]:
/* ヒント */
(O.r) . (O.r)$
trigsimp(%)$

Maxima-Jupyter によるグラフ作成

Maxima-Jupyter を使って，関数のグラフを描くことができます。また，数値データもグラフにすることができます。

In [135]:
/* Jupyter Notebook にインラインでグラフを表示させる場合，*/
/* 最初に以下のようにプロットオプションをセット。 */
set_plot_option([svg_file, "~/.maxplot.svg"])$

2 次元グラフ plot2d の例

2 次元グラフ $y = f(x)$ を描く一般的な表記例は以下の通りです。

plot2d(f(x), [x, a, b])

例として，$y = \sin x$ のグラフを $−2\pi \leq x \leq 2\pi$ の範囲で描きます。基本的な定数の一つである円周率 $\pi$ は Maxima では %pi と書くのでしたね。

In [136]:
plot2d(sin(x), [x, -2*%pi, 2*%pi])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 sin(x) x gnuplot_plot_1 -1 -0.5 0 0.5 1 -6 -4 -2 0 2 4 6

3 次元グラフ plot3d の例

3 次元グラフ $z = g(x, y)$ を描く一般的な表記例は以下の通りです。

plot3d(g(x,y), [x, a, b], [y, c, d])

例として，$z = x \sin y$ のグラフを $-3 \leq x \leq 3, -4 \leq y \leq 4$ の範囲で描きます。

In [137]:
plot3d(x*sin(y), [x, -3, 3], [y, -4, 4])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 -3 -2 -1 0 1 2 3 -4 -3 -2 -1 0 1 2 3 4 -3 -2 -1 0 1 2 3 gnuplot_plot_1 x*sin(y) x y z

数値データ・リストのグラフ作成例

Maxima は，リスト形式のリスト形式の数値データもグラフ化することができます。

以下の例では，最初（左側）の数値を $x$ 座標の値，次（右側）の数値を $y$ 座標の値として 6 個の点 からなるリスト data の各点をつないだ折れ線グラフを描きます。

In [138]:
data: makelist([i, i^2], i, 0, 5);
plot2d([discrete, data])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x gnuplot_plot_1 0 5 10 15 20 25 0 1 2 3 4 5
Out[138]:
\[\tag{${\it \%o}_{188}$}\left[ \left[ 0 , 0 \right] , \left[ 1 , 1 \right] , \left[ 2 , 4 \right] , \left[ 3 , 9 \right] , \left[ 4 , 16 \right] , \left[ 5 , 25 \right] \right] \]

オプションを設定してプロットする例。

ここでは，[style, points]を設定して線でつながずに点で描きます。プロットオプションの style には，points の他にも，lines，linespoints， dots が設定できます。

In [139]:
plot2d([discrete, data], [style, points])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x gnuplot_plot_1 0 5 10 15 20 25 0 1 2 3 4 5

でかい点ですね。点のサイズを変更して描きます。

In [140]:
plot2d([discrete, data], [style, [points, 1.5]])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x gnuplot_plot_1 0 5 10 15 20 25 0 1 2 3 4 5

複数のグラフを重ねて表示

Maxima で複数のグラフを重ねて表示する例を示します。

$y = x^2 - 1$ と $y = 4 x - 5$ の 2 つのグラフを重ねて描きます。

$x$ の範囲は $-5 \leq x \leq 5$ です。 以下の例でわかるように，重ねて描きたい関数を [x^2 - 1, 4*x - 5] のように [ と ] で囲んだリスト形式にして plot2d コマンドを使います。

In [141]:
plot2d([x^2 - 1, 4*x - 5], [x, -5, 5])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x x^2-1 x^2-1 4*x-5 4*x-5 -25 -20 -15 -10 -5 0 5 10 15 20 25 -4 -2 0 2 4

いくつかオプションを設定して描く例です。

以下の例では，縦軸 ($y$ 軸) の表示範囲を制限し たために，

plot2d: some values were clipped. というメッセージが出ています。

In [142]:
plot2d([x^2 - 1, 4*x - 5], [x, -5, 5],
       [y, -5, 10],                         /* 縦軸の表示範囲の設定 */
       [color, red, black],                 /* 線の色の設定 */ 
       [style, [lines, 4], lines],          /* 片方の線の太さを4に */
       [gnuplot_preamble, "set key bottom"] /* 凡例の位置 */
       )$

plot2d: some values were clipped.
plot2d: some values were clipped.
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x x^2-1 x^2-1 4*x-5 4*x-5 -4 -2 0 2 4 6 8 10 -4 -2 0 2 4

上のグラフをみると，2 つのグラフは 1 点で接しているように見えます。

実際に $y = 4x - 5$ が接線であることを示してみましょう。

$x^2 - 1 = 4 x - 5$ の解が1つであることを示せば十分ですね。

In [143]:
sol: solve(x^2 - 1 = 4*x - 5, x);
Out[143]:
\[\tag{${\it \%o}_{194}$}\left[ x=2 \right] \]

$y = f(x)$ の $x = x_1$ における接線の方程式は， $$ y - f(x_1) = f'(x_1) \,(x - x_1)$$ ですから...

In [144]:
f(x):= x^2 - 1;
define(df(x), diff(f(x), x));

x1: rhs(sol[1]);
y = df(x1) * (x - x1) + f(x1), ratsimp;
Out[144]:
\[\tag{${\it \%o}_{195}$}f\left(x\right):=x^2-1\]
Out[144]:
\[\tag{${\it \%o}_{196}$}{\it df}\left(x\right):=2\,x\]
Out[144]:
\[\tag{${\it \%o}_{197}$}2\]
Out[144]:
\[\tag{${\it \%o}_{198}$}y=4\,x-5\]

できたら，$y = x2 - 1$ の $x = 1$ 等における接線のグラフも描いてみましょう。

数値データファイルを読み込む

Maxima では，あらかじめ作成された数値データファイルを読み込んでグラフを描くこともできます。

以下のような内容のファイル test.dat がカレントディレクトリにあるとします。

0   0
1   1
2   4
3   9
4   16
5   25

データファイルを読み込む Maxima の関数は，read_nested_list を使います。

In [145]:
dat: read_nested_list("test.dat");
Out[145]:
\[\tag{${\it \%o}_{199}$}\left[ \left[ 0 , 0 \right] , \left[ 1 , 1 \right] , \left[ 2 , 4 \right] , \left[ 3 , 9 \right] , \left[ 4 , 16 \right] , \left[ 5 , 25 \right] \right] \]
In [146]:
plot2d([discrete, dat],
       [x, 0, 6], [y, 0, 28],                   /* x, y の表示範囲を設定 */ 
       [style, [points, 1]], [color, red],      /* 大きさ，色 */
       [gnuplot_preamble, "set key top left"],  /* 凡例の位置 */ 
       [legend, "データ"]                       /* 凡例表示の設定 */
       )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x データ データ 0 5 10 15 20 25 0 1 2 3 4 5 6

数値データと理論曲線を重ねて表示

前節の数値データファイル test.dat と理論曲線 $y = x^2$ の 2 つのグラフを重ねて表示してみます。

In [147]:
plot2d([[discrete, dat], x^2], [x, 0, 5], [y, 0, 28],
       [style, [points, 1.5], lines], [color, red, blue],
       [gnuplot_preamble, "set key top left"], 
       [legend, "データ", "理論曲線 y=x^2"]
       )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x データ データ 理論曲線 y=x^2 理論曲線 y=x^2 0 5 10 15 20 25 0 1 2 3 4 5

媒介変数表示の 2 次元グラフ

半径 $1$ の円の方程式は $x^2 +y^2 = 1$ です.この円を描くには，$y = \pm \sqrt{1 - x^2}$ として $y = f(x)$ の形にするよりも，以下のような媒介変数表示にしたほうが簡単でしょう。

$$ x=\cos t, \quad y=\sin t \quad (0 \leq t \leq 2\pi) $$

媒介変数表示の 2 次元グラフを Maxima で描くには以下のようにします。

In [148]:
plot2d([parametric, cos(t), sin(t), [t, 0, 2*%pi]])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 sin(t) cos(t) gnuplot_plot_1 -1 -0.5 0 0.5 1 -1 -0.5 0 0.5 1

グラフの縦横の 比を1:1にして円らしく見えるように，[same_xy] を設定してみます。

[yx_ratio, 1] でも同等です。

In [149]:
plot2d([parametric, cos(t), sin(t), [t, 0, 2*%pi]],
        [same_xy],
        [xlabel, "x"], [ylabel, "y"], [legend, "x^2+y^2=1"],
        [x,-1.1, 1.1], [y, -1.1, 1.1]
      )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x x^2+y^2=1 x^2+y^2=1 -1 -0.5 0 0.5 1 -1 -0.5 0 0.5 1

練習

（練習）楕円のグラフ（楕円中心を原点にして）

同様にして，楕円のグラフを描くこともできます。 原点を中心とし，長半径 $a$，単半径 $b$ の楕円の式は

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$

媒介変数表示では，$x=a \cos t, \ y=b \sin t, \ (0\leq t\leq 2\pi)$と書けます。 $a$，$b$ に適当な値を入れて楕円のグラフを描きなさい。

In [150]:
/* ヒント */
x(a, t):= a*cos(t)$
y(b, t):= b*sin(t)$

plot2d([parametric, x(1,t), y(1,t), [t, 0, 2*%pi]],
        [same_xy],
        [xlabel, "x"], [ylabel, "y"], [legend, "a=1, b=1"],
        [x,-2, 2], [y, -2, 2]
      )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x a=1, b=1 a=1, b=1 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2

海王星と冥王星の軌道

焦点を原点とした楕円のグラフ

太陽からの万有引力を受けて運動する惑星は，太陽（二体問題では質量中心）を焦点の一つとした楕円運動を描いて運動します。 焦点の一つを原点とし，長半径 $a$，離心率 $e$ の楕円の方程式は，極座標 $r$，$\varphi$ を使って以下のように表すことができます。

$$ r= \frac{a (1−e^2)}{ 1 + e\cos\varphi}$$

さて，かつては第9惑星，現在では準惑星の一つである冥王星も楕円軌道を描きます。冥王星の軌道長半径 $𝑎_P=39.767\mbox{AU}$，離心率 $𝑒_P=0.254$ を使って冥王星の軌道を描きます。

まず，極座標表示の楕円の式を関数として定義します。

In [151]:
r(a, e, t):= a*(1-e^2)/(1+e*cos(t))$
x(a, e, t):= r(a, e, t)*cos(t)$
y(a, e, t):= r(a, e, t)*sin(t)$
In [152]:
aP: 39.767$
eP: 0.254$
plot2d([parametric, x(aP, eP, t), y(aP, eP, t), [t, 0, 2*%pi]],
        [same_xy],
        [xlabel, "x"], [ylabel, "y"], [legend, "冥王星"],
        [x,-50, 50], [y, -50, 50]
      )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x 冥王星 冥王星 -40 -20 0 20 40 -40 -20 0 20 40

では，この冥王星の軌道と，その内側をまわる海王星の軌道を重ねて描いてみましょう。

海王星の軌道長半径は $a_N=30.1104\mbox{AU}$，離心率は $e_N=0.0090$ と小さいので簡単のために $e_N=0$ として扱います。実際の2つの天体の軌道は同じ平面上にありませんが，太陽からの距離のみをみるために，ここでは同一平面上に描きます。

In [153]:
aN: 30.1104$
eN: 0$
plot2d([[parametric, x(aP, eP, t), y(aP, eP, t), [t, 0, 2*%pi]],
        [parametric, x(aN, eN, t), y(aN, eN, t), [t, 0, 2*%pi]]
       ],
        [same_xy],
        [xlabel, "x"], [ylabel, "y"], [legend, "冥王星", "海王星"],
        [x,-50, 50], [y, -50, 50]
      )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x 冥王星 冥王星 海王星 海王星 -40 -20 0 20 40 -40 -20 0 20 40

さて，この冥王星と海王星の軌道のグラフをいると，軌道が交差しているように見えます。このことを確かめます。

表示される領域を制限して，交差しているあたりを拡大してみます。

In [154]:
plot2d([[parametric, x(aP, eP, t), y(aP, eP, t), [t, 0, 2*%pi]],
        [parametric, x(aN, eN, t), y(aN, eN, t), [t, 0, 2*%pi]]
       ],
        [xlabel, "x"], [ylabel, "y"], [legend, "冥王星", "海王星"],
        [x, 27, 29], [y, 10, 13]
      )$

plot2d: some values were clipped.
plot2d: some values were clipped.
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x 冥王星 冥王星 海王星 海王星 10 10.5 11 11.5 12 12.5 13 27 27.5 28 28.5 29

海王星の軌道は半径 $a_N$ の円としますから，以下の式を満たす角度 $\varphi$ を求めればよいことになります。

$$ r(a_P, e_P, \varphi) = a_N$$

$0 < \varphi < \pi/2$ のどこかで交差しているようですから，このあたりで数値的に解を求める方法は以下の通りです。

In [155]:
phi1: find_root(r(aP, eP, t) = aN, t, 0, %pi/2);
Out[155]:
\[\tag{${\it \%o}_{217}$}0.3840242513908817\]

$ -\pi/2 < \varphi < 0$ の範囲でも交差していますね。 対称性から答えは phi1 に負号をつけたものになるのは明らかですが，念のために確かめます。

In [156]:
phi2: find_root(r(aP, eP, t) = aN, t, -%pi/2, 0);
Out[156]:
\[\tag{${\it \%o}_{218}$}-0.3840242513908817\]

求めた角度はラジアン単位ですから，度に直してみます。

In [157]:
fpprintprec: 3$ /* 表示するケタ数を 3 に */ 
float(phi1*180/%pi);
Out[157]:
\[\tag{${\it \%o}_{220}$}22.0\]

この角度の 2 倍，つまり一周 360 度のうちに約 44 度にあたる分は海王星のほうが冥王星より 太陽から遠い位置にあることがわかります。

原点と 2 つの軌道の交点を結ぶ直線を描く方法は以下の通りです。

In [158]:
plot2d([[discrete, [[0, 0], [aN*cos(phi1), aN*sin(phi1)]]],
        [discrete, [[0, 0], [aN*cos(phi2), aN*sin(phi2)]]]
       ],
        [same_xy], [x,-50, 50], [y, -50, 50], 
        [xlabel, "x"], [ylabel, "y"], [legend, "", ""],
        [color, black, black]
      )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x gnuplot_plot_1 gnuplot_plot_2 -40 -20 0 20 40 -40 -20 0 20 40

原点と2つの軌道の交点を結ぶ直線を追加して，冥王星と海王星の軌道を描いてみます。

In [159]:
plot2d([[discrete, [[0, 0], [aN*cos(phi1), aN*sin(phi1)]]],
        [discrete, [[0, 0], [aN*cos(phi2), aN*sin(phi2)]]],
        [parametric, x(aP, eP, t), y(aP, eP, t), [t, 0, 2*%pi]],
        [parametric, x(aN, eN, t), y(aN, eN, t), [t, 0, 2*%pi]]
       ],
        [same_xy], [x,-50, 50], [y, -50, 50], 
        [xlabel, "x"], [ylabel, "y"], [legend, "", "", "冥王星", "海王星"],
        [color, black, black, red, blue]
      )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x gnuplot_plot_1 gnuplot_plot_2 冥王星 冥王星 海王星 海王星 -40 -20 0 20 40 -40 -20 0 20 40

月別平年気温の関数フィット

青森市の月別平年気温のデータを使って行列 M を作ります。

In [160]:
M: read_matrix("aomori.dat");
Out[160]:
\[\tag{${\it \%o}_{223}$}\begin{pmatrix}1 & -1.2 \\ 2 & -0.7 \\ 3 & 2.4 \\ 4 & 8.3 \\ 5 & 13.3 \\ 6 & 17.2 \\ 7 & 21.1 \\ 8 & 23.3 \\ 9 & 19.3 \\ 10 & 13.1 \\ 11 & 6.8 \\ 12 & 1.5 \\ \end{pmatrix}\]

このデータをグラフに描いてみます。

数値データをグラフにする際には，すでに説明したように plot2d([discrete, ... ]) を使いますが，使用するデータはリスト形式である必要があります。 今回は，すぐ後で述べる理由により，行列形式でデータを準備したので，args 関数を使って行列をリストに変換して plot2d に渡します。

In [161]:
plot2d([discrete, args(M)], [style, [points, 1.5]])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x gnuplot_plot_1 -5 0 5 10 15 20 25 0 2 4 6 8 10 12

グラフを見ると，月別平年気温は 12 ヶ月周期の三角関数でフィットできるようにみえます。

では，以下のように関数フィットをしてみましょう。

まず，最小二乗法のパッケージ lsquares をロードします.これは lsquares_estimates を 初めて使う際，最初に 1 回だけ行えばよいです。

In [162]:
load(lsquares)$

次に，次のような関数を定義して，うまくフィットするように定数 a, b, c を求めます。

最小二乗法を行う関数 lsquares_estimates には数値データを行列として入れてやる必要があります。このために行列形式で月別平年気温のデータを準備したのでした。

In [163]:
kill(a0, a1, b1, f)$
f(x) := a0 + a1*cos(2*%pi*x/12) + b1*sin(2*%pi*x/12);
Out[163]:
\[\tag{${\it \%o}_{227}$}f\left(x\right):=a_{0}+a_{1}\,\cos \left(\frac{2\,\pi\,x}{12}\right)+b_{1}\,\sin \left(\frac{2\,\pi\,x}{12}\right)\]
In [164]:
lsquares_estimates(M, [x, y], y=f(x), [a0, a1, b1])$
float(%);
Out[164]:
\[\tag{${\it \%o}_{229}$}\left[ \left[ a_{0}=10.4 , a_{1}=-8.37 , b_{1}=-8.29 \right] \right] \]

最小二乗法によって求めた a0, a1, b1 の値を f(x) に代入し，この関数を描きます。

In [165]:
fit: ev(f(x), %);
Out[165]:
\[\tag{${\it \%o}_{230}$}-8.29\,\sin \left(\frac{\pi\,x}{6}\right)-8.37\,\cos \left(\frac{\pi\,x}{6}\right)+10.4\]
In [166]:
plot2d(fit, 
       [x, 0.5, 12.5], [y, -5, 28],
       [style,lines], [color, red],
       [gnuplot_preamble, "set xtics 1"],
       [xlabel, "月"], [ylabel, "月別平年気温"], [title, "青森市の月別平年気温"]
     )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 月別平年気温 月 gnuplot_plot_1 -5 0 5 10 15 20 25 1 2 3 4 5 6 7 8 9 10 11 12 青森市の月別平年気温

最終的に，月別平年気温の数値データとフィット曲線を重ねて描いてみます。

In [167]:
plot2d([[discrete, args(M)], fit],
       [x, 0.5, 12.5], [y, -5, 28],
       [style, [points, 1.5], [lines, 2]], [color, blue, red],
       [gnuplot_preamble, "set xtics 1; set key samplen 1"],
       [legend, "気温データ", "フィット曲線"],
       [xlabel, "月"], [ylabel, "月別平年気温"], [title, "青森市の月別平年気温"]
     )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 月別平年気温 月 気温データ 気温データ フィット曲線 フィット曲線 -5 0 5 10 15 20 25 1 2 3 4 5 6 7 8 9 10 11 12 青森市の月別平年気温

ちなみに，関数フィットした際の定数 a0 は月別平均気温の平均値に相当します。 平均値を求めるだけなら，最小二乗法などやらなくても以下のようにして求めることができます。

In [168]:
sum(M[i,2], i, 1, length(M))/length(M);
Out[168]:
\[\tag{${\it \%o}_{233}$}10.4\]

Maxima-Jupyter を使ってもう少し...

Maxima を使って，さらにいくつか問題に取り組んでみます。

波動

x 方向に進む波

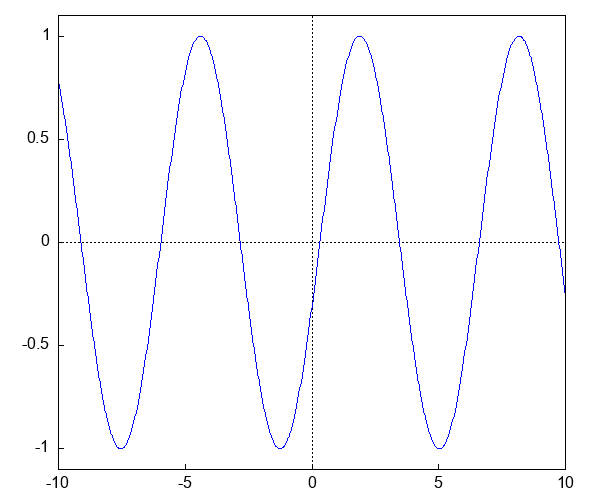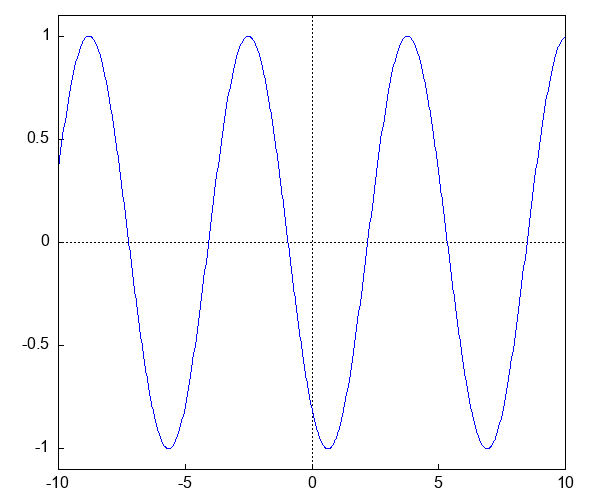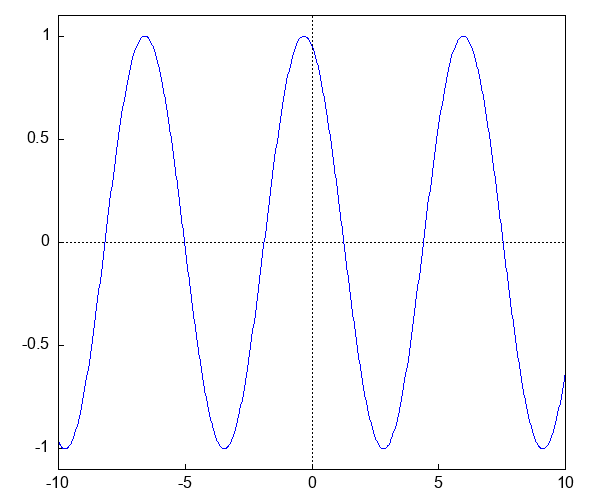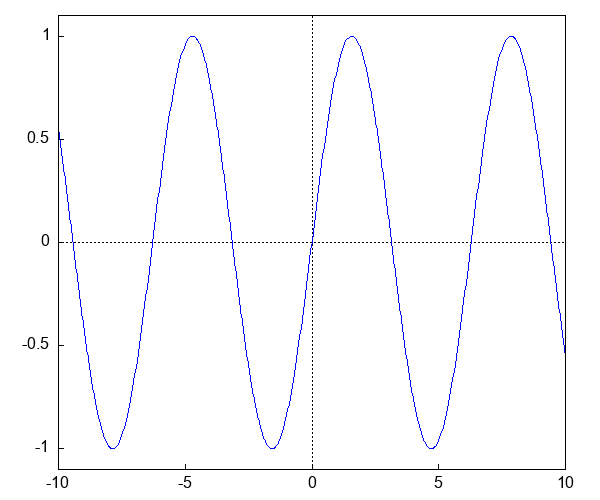
$\sin(x - v t)$ は$x$の正の方向に速度$v$で進む正弦型の波動をあらわす。 波が進む様子を描いてみよう。

簡単のために，$v = 1$ とする。時刻 $t=0$ では，この波は $\sin x$。少し時間がたった後，たとえば $t = 0.5$ では，$\sin (x - 0.5)$，さらに，$\sin (x - 1.0)$，，$\sin (x - 1.5)$ など...

In [169]:
/* Jupyter Notebook にインラインでグラフを表示させる場合，*/
/* 最初に以下のようにプロットオプションをセット。 */
set_plot_option([svg_file, "maxplot.svg"])$
In [170]:
plot2d(sin(x), 
       [x, -10, 10], [y, -1.1, 1.1],  
       [style, [lines,2]], [color, red],
       [xlabel, "x"], [ylabel, ""],
       [gnuplot_preamble, "set key outside; set key samplen 1"], 
       [legend, "t = 0.0"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x t = 0.0 t = 0.0 -1 -0.5 0 0.5 1 -10 -5 0 5 10
In [171]:
plot2d([sin(x), sin(x - 0.5)], 
       [x, -10, 10], [y, -1.1, 1.1],  
       [style, dots, [lines, 2, 2]], 
       [xlabel, "x"], [ylabel, ""],
       [gnuplot_preamble, "set key outside; set key samplen 1"], 
       [legend, "t = 0.0", "t = 0.5"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x t = 0.0 t = 0.0 t = 0.5 t = 0.5 -1 -0.5 0 0.5 1 -10 -5 0 5 10
In [172]:
plot2d([sin(x), sin(x - 0.5), sin(x - 1.0)], 
       [x, -10, 10], [y, -1.1, 1.1],  
       [style, dots, dots, [lines, 2, 2]], 
       [xlabel, "x"], [ylabel, ""],
       [gnuplot_preamble, "set key outside; set key samplen 1"], 
       [legend, "t = 0.0", "t = 0.5", "t = 1.0"]
       )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x t = 0.0 t = 0.0 t = 0.5 t = 0.5 t = 1.0 t = 1.0 -1 -0.5 0 0.5 1 -10 -5 0 5 10
In [173]:
plot2d([sin(x), sin(x - 0.5), sin(x - 1.0), sin(x - 1.5)], [x, -10, 10], [y, -1.1, 1.1],  
       [style, dots, dots, dots, [lines, 2, 2]], 
       [xlabel, "x"], [ylabel, ""],
       [gnuplot_preamble, "set key outside; set key samplen 1"], 
       [legend, "t = 0.0", "t = 0.5", "t = 1.0", "t = 1.5"]
       )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x t = 0.0 t = 0.0 t = 0.5 t = 0.5 t = 1.0 t = 1.0 t = 1.5 t = 1.5 -1 -0.5 0 0.5 1 -10 -5 0 5 10

draw で GIF アニメ

draw 関数を使うことで，Jupyter Notebook 環境で簡単にアニメーションを作ることができる。

In [174]:
draw(
  terminal   = animated_gif,
  dimensions = [400, 300], 
  delay      = 10,
  file_name  = "anim1",
  makelist(gr2d(explicit(sin(x - 0.314*i), x, -10, 10)), i, 20)
  )$

$x$ 軸，$y$ 軸を描き，縦軸の表示範囲を [-1.1, 1.1] に設定し，少し早く動く GIF アニメにしてみます。

In [175]:
draw(
  terminal   = animated_gif, 
  delay      = 5,
  file_name  = "anim2",
  makelist(gr2d(explicit(sin(x - 0.314*i), x, -10, 10), 
                yrange = [-1.1, 1.1], xaxis = true, yaxis = true
               ), i, 20)
  )$

うなり

振動数が少しだけ異なる2つの波を重ね合わせると「うなり」が起こることを示してみます。（高校の物理で習ったと思いますが，三角関数の加法則との関連で説明してみます。）

In [176]:
plot2d(sin(x + 0.05*x) + sin(x - 0.05*x), [x, -100, 100], [y, -2.1, 2.1], 
       [xlabel, ""], [ylabel, ""], 
       [gnuplot_preamble, "set key below"], [legend, "sin(x + 0.05*x) + sin(x - 0.05*x)"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 sin(x + 0.05*x) + sin(x - 0.05*x) sin(x + 0.05*x) + sin(x - 0.05*x) -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -100 -50 0 50 100
In [177]:
sin(a + b) + sin(a - b), trigexpand;
Out[177]:
\[\tag{${\it \%o}_{242}$}2\,\sin a\,\cos b\]

... ですから，うなりとなる波形は $2 \cos b = 2 \cos 0.05x$ と早合点してしまいそうですが，これを描いてみると...

In [178]:
plot2d([sin(x + 0.05*x) + sin(x - 0.05*x), 2*cos(0.05*x)], 
       [x, -100, 100], [y, -2.1, 2.1], 
       [style, lines, [lines, 2, 2]],
       [xlabel, ""], [ylabel, ""], 
       [gnuplot_preamble, "set key below"], 
       [legend, "sin(x + 0.05x) + sin(x - 0.05x)", "2 cos 0.05x"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 sin(x + 0.05x) + sin(x - 0.05x) sin(x + 0.05x) + sin(x - 0.05x) 2 cos 0.05x 2 cos 0.05x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -100 -50 0 50 100

そうではなくて，むしろ $2 |\cos 0.05x|$ ですよね。

In [179]:
plot2d([sin(x + 0.05*x) + sin(x - 0.05*x), 2*abs(cos(0.05*x))], 
       [x, -100, 100], [y, -2.1, 2.1], 
       [style, lines, [lines, 2, 2]],
       [xlabel, ""], [ylabel, ""], 
       [gnuplot_preamble, "set key below"], 
       [legend, "sin(x + 0.05x) + sin(x - 0.05x)", "2 |cos 0.05x|"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 sin(x + 0.05x) + sin(x - 0.05x) sin(x + 0.05x) + sin(x - 0.05x) 2 |cos 0.05x| 2 |cos 0.05x| -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -100 -50 0 50 100

つまり，$\omega_1 = a+b, \omega_2 = a-b$ の波を重ねると， 振動数の差の半分 $\displaystyle b = \frac{\omega_1 - \omega_2}{2}$ の コサイン波 $2 \cos b t$ が生じるように思えるが...

実際には，その絶対値 $2 | \cos b t|$ なので，振動数は実質その2倍，つまり うなりの振動数は $2 b = \omega_1 - \omega_2$ となり，

「振動数のわずかに異なる2つの波を重ねると，それらの振動数の差の振動数をもつうなりが発生する」

ということになる，という理解でどうでしょう。

定常波

波長・振幅が等しい正弦波が直線上を逆向きに同じ速さで進んでいると，重ね合わせによってどのような波が生じるか。

$$ \sin (x- v t) + \sin(x + v t)$$

例を参考に，GIF アニメを作ってみてください。

In [180]:
plot2d(sin(x - 0) + sin(x + 0), 
       [x, -10, 10], [y, -2.1, 2.1],  
       [style, [lines, 3, red]], 
       [xlabel, ""], [ylabel, ""],
       [gnuplot_preamble, "set key outside; set key samplen 1"], 
       [legend, "t = 0.0"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 t = 0.0 t = 0.0 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -10 -5 0 5 10
In [181]:
plot2d([sin(x - 0) + sin(x + 0), sin(x - 0.5) + sin(x + 0.5)],
       [x, -10, 10], [y, -2.1, 2.1],  
       [style, dots, [lines, 3, red]], 
       [xlabel, ""], [ylabel, ""],
       [gnuplot_preamble, "set key outside; set key samplen 1"], 
       [legend, "t = 0.0", "t = 0.5"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 t = 0.0 t = 0.0 t = 0.5 t = 0.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -10 -5 0 5 10
In [182]:
plot2d([sin(x - 0) + sin(x + 0), 
        sin(x - 0.5) + sin(x + 0.5), 
        sin(x - 1.0) + sin(x + 1.0)],
       [x, -10, 10], [y, -2.1, 2.1],  
       [style, dots, dots, [lines, 3, red]], 
       [xlabel, ""], [ylabel, ""],
       [gnuplot_preamble, "set key outside; set key samplen 1"], 
       [legend, "t = 0.0", "t = 0.5", "t = 1.0"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 t = 0.0 t = 0.0 t = 0.5 t = 0.5 t = 1.0 t = 1.0 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -10 -5 0 5 10
In [183]:
plot2d([sin(x - 0) + sin(x + 0), 
        sin(x - 0.5) + sin(x + 0.5), 
        sin(x - 1.0) + sin(x + 1.0), 
        sin(x - 1.5) + sin(x + 1.5)],
       [x, -10, 10], [y, -2.1, 2.1],  
       [style, dots, dots, dots, [lines, 3, red]], 
       [xlabel, ""], [ylabel, ""],
       [gnuplot_preamble, "set key outside; set key samplen 1"], 
       [legend, "t = 0.0", "t = 0.5", "t = 1.0", "t = 1.5"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 t = 0.0 t = 0.0 t = 0.5 t = 0.5 t = 1.0 t = 1.0 t = 1.5 t = 1.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 -10 -5 0 5 10
In [184]:
draw(
  terminal   = animated_gif, 
  delay      = 10,
  file_name  = "anim3",
  makelist(gr2d(explicit(sin(x - 0.0628*i) + sin(x + 0.0628*i), x, -10, 10), 
                yrange = [-2.1, 2.1], xaxis = true, yaxis = true
               ), i, 100)
  )$

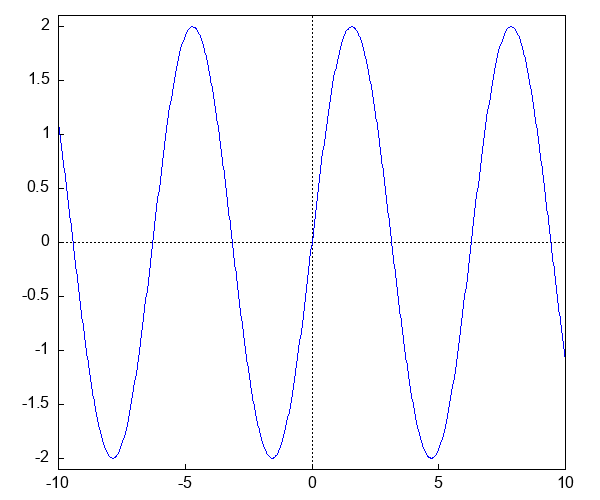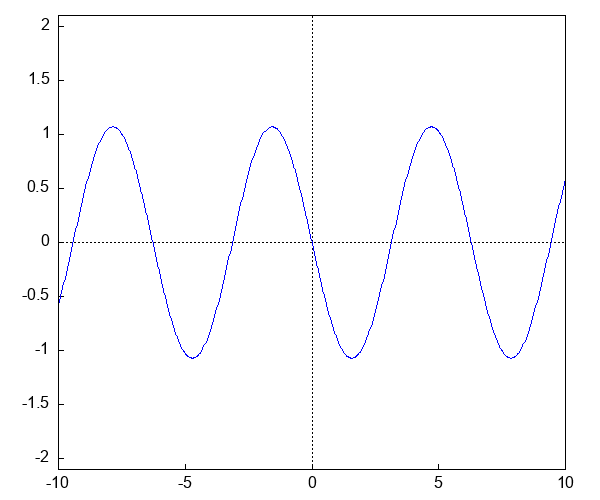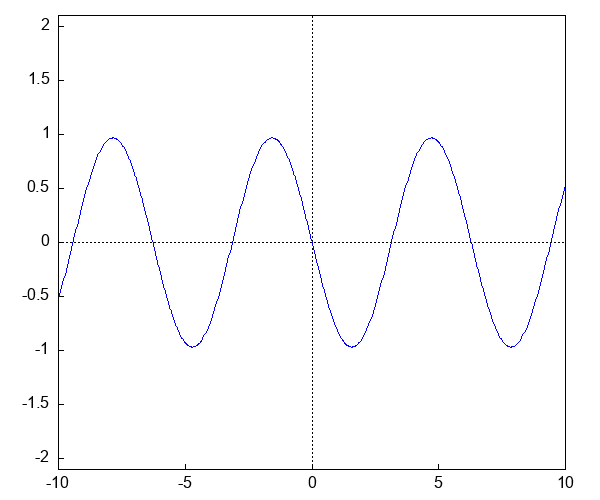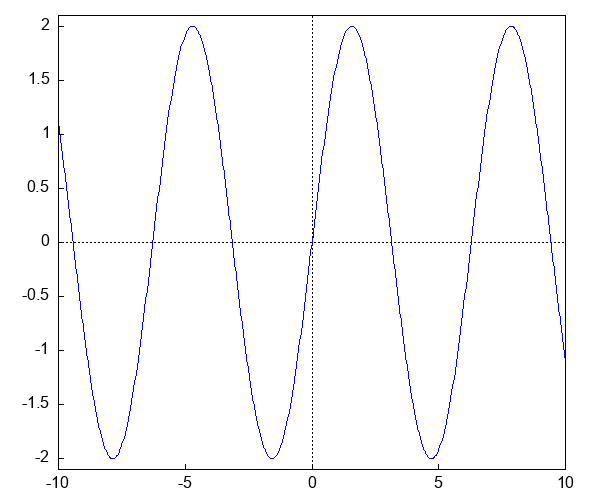
一様重力場中の質点の運動

水平な地上で，水平となす角 $\theta$ で斜め上方に初速度の大きさ $v_0$ でボールを投げ出す。 $v_0$ を一定としたとき，水平到達距離を最大にする $\theta$ は？ またそのときの水平到達距離は？

水平方向を $x$，鉛直上向きを $y$ をすると，運動方程式は，

$$\frac{d^2 x}{dt^2} = 0, \quad \frac{d^2 y}{dt^2} = -g$$

初期条件を $t = 0$ で $x(0) = 0, y(0) = 0, v_x(0) = v_0 \cos\theta, v_y(0) = v_0 \sin\theta$ として解きます。

In [185]:
ode2('diff(x, t, 2)  = 0, x, t)$
ic2(%, t = 0, x = 0, 'diff(x, t) = v[0]*cos(theta));
Out[185]:
\[\tag{${\it \%o}_{251}$}x=v_{0}\,t\,\cos \vartheta\]
In [186]:
ode2('diff(y, t, 2) = -g, y, t)$
ic2(%, t = 0, y = 0, 'diff(y, t) = v[0]*sin(theta));
Out[186]:
\[\tag{${\it \%o}_{253}$}y=v_{0}\,t\,\sin \vartheta-\frac{g\,t^2}{2}\]

... となるが，$g$ や $v_0$ に実際の次元のついた量をいれるのではなく，まずはこの式を，この系に特徴的な量で無次元化することを考える。

今，$\displaystyle \theta=\frac{\pi}{2}$ として垂直に投げ上げると，鉛直方向の $y$ は

$$ y = v_0 t - \frac{1}{2} g t^2 = \frac{v_0^2}{2 g} - \frac{1}{2} g \left( t - \frac{v_0}{g}\right)^2 $$

となることから，特徴的な量として，$y$ が最大値をとる時刻 $\displaystyle t_m \equiv \frac{v_0}{g}$ と，その時の $y$ の最大値 $\displaystyle y_m \equiv \frac{v_0^2}{2g}$ を使って，以下のような無次元量をつくる。

$$ \bar{x} \equiv \frac{x}{y_m}, \quad \bar{y} \equiv \frac{y}{y_m}, \quad \bar{t} \equiv \frac{t}{t_m}$$

これらの無次元量を使って軌道をあらわすと，

$$ \bar{x} = 2 \bar{t} \cos\theta, \quad \bar{y} = 2 \bar{t} \sin\theta - \bar{t}^2 $$

以後は簡単のために $\bar{\ }$（バー）を省略する。

$\theta$ の値を変えて，$t$ を媒介変数としたグラフをいくつか描いてみる。

In [187]:
x(theta, t):= 2*t*cos(theta);
y(theta, t):= 2*t*sin(theta) - t**2;
Out[187]:
\[\tag{${\it \%o}_{254}$}x\left(\vartheta , t\right):=2\,t\,\cos \vartheta\]
Out[187]:
\[\tag{${\it \%o}_{255}$}y\left(\vartheta , t\right):=2\,t\,\sin \vartheta-t^2\]
In [188]:
th: %pi/4$
plot2d([parametric, x(th, t), y(th, t), [t, 0, 2]], 
       [xlabel, "x"], [ylabel, "y"], [legend, "θ = π/4"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x θ = π/4 θ = π/4 -1.2 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0 0.5 1 1.5 2 2.5 3

媒介変数 $t$ の範囲を適当に [0:2] とした図が上図であるが，$y$ の値がマイナスの領域まで描いてしまって，このボールが地面にめり込んでしまっている！！

$\displaystyle y = 2 t \sin\theta - t^2 = 0 $ から $t$ の範囲は $\theta$ によって異なり，$0 \le t \le 2 \sin\theta$ であることがわかるので， 以下のようにして，地面にめりこまないように，$y$ がふたたび $0$ になる時刻までのプロットにする。

In [189]:
th: %pi/4$
plot2d([parametric, x(th, t), y(th, t), [t, 0, 2*sin(th)]], 
       [xlabel, "x"], [ylabel, "y"], [legend, "θ = π/4"], 
       [xtics, 0.2], [ytics, 0.2], grid2d,
       [x, 0, 2], [y, 0, 1], [yx_ratio, 0.5])$

plot2d: some values were clipped.
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x θ = π/4 θ = π/4 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

初速度の角度を変え，いくつかプロット。

In [190]:
th1: %pi/6$
th2: %pi/5$
th3: %pi/4$
th4: %pi/3$
plot2d([[parametric, x(th1, t), y(th1, t), [t, 0, 2*sin(th1)]], 
        [parametric, x(th2, t), y(th2, t), [t, 0, 2*sin(th2)]], 
        [parametric, x(th3, t), y(th3, t), [t, 0, 2*sin(th3)]], 
        [parametric, x(th4, t), y(th4, t), [t, 0, 2*sin(th4)]]], 
       [xlabel, "x"], [ylabel, "y"], grid2d,
       [legend, "θ = π/6", "θ = π/5", "θ = π/4", "θ = π/3"], 
       [xtics, 0.2], [ytics, 0.2], [gnuplot_preamble, "set grid"],
       [x, 0, 2], [y, 0, 1], [yx_ratio, 0.5])$

plot2d: some values were clipped.
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 y x θ = π/6 θ = π/6 θ = π/5 θ = π/5 θ = π/4 θ = π/4 θ = π/3 θ = π/3 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

さて，肝心の水平到達距離を最大にする $\theta$ だが，地上から投げ上げたボールが再び地上に戻ってくるまでの時間は，$y(\theta, t) = 0$ を $t$ について解いて...

In [191]:
solt: solve(y(theta,t) = 0, t);
Out[191]:
\[\tag{${\it \%o}_{265}$}\left[ t=2\,\sin \vartheta , t=0 \right] \]

$t = 2 \sin\theta$ をあらためて $x(\theta, t)$ に代入して...

In [192]:
x(theta, t), solt[1];
trigreduce(%);
Out[192]:
\[\tag{${\it \%o}_{266}$}4\,\cos \vartheta\,\sin \vartheta\]
Out[192]:
\[\tag{${\it \%o}_{267}$}2\,\sin \left(2\,\vartheta\right)\]

これから，ただちに $x$ は $\theta=\pi/4$ のとき最大値 $2$ をとることがわかる。

あたらめて無次元化するまえの $x$ についてみると，最大到達距離は

$$x_{\max} = \bar{x}_{\max} \, y_m = 2 \times \frac{v_0^2}{2g} = \frac{v_0^2}{g}$$

ケプラーの第3法則

以下のような内容のファイル planets.dat がカレント・ディレクトリにあるとします。

  0.3841  0.24085
  0.7233  0.61520
  1.0000  1.00002
  1.5237  1.88085
  5.2026  11.8620
  9.5549  29.4572
19.2184   84.0205
30.1104  164.7701
39.767   248

1列目の軌道長半径を x に，2列目の平均周期を y にしてプロットしてみます。

In [193]:
dat: read_nested_list("planets.dat")$

以下では，離散データ dat をプロットするので，[style, [points, 1.5, red]] のように points でプロットすること，および点のサイズと色を指定しています。また，grid2d でグリッド線を表示させています。

In [194]:
plot2d([discrete, dat], [style, [points, 1.5, red]], grid2d,
       [xlabel, "軌道長半径 a"], [ylabel, "公転周期 T"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 公転周期 T 軌道長半径 a gnuplot_plot_1 0 50 100 150 200 250 0 5 10 15 20 25 30 35 40

対数グラフ

上のグラフを見る限りは，直線で禁じできるような単純な比例関係ではなさそうです。

以下のように，logx, logy, として両対数グラフにしてみます。

In [195]:
plot2d([discrete, dat], [style, [points, 1.5, red]], grid2d, logx, logy,
       [xlabel, "軌道長半径 a"], [ylabel, "公転周期 T"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 公転周期 T 軌道長半径 a gnuplot_plot_1 0.1 1 10 100 1000 1 10

両対数グラフにすると，データは直線に乗っているようにみえます。ということは， $\displaystyle T = K a^p$ のような関係になっていることが予想されます。

また，$a = 1$ のとき $T=1$ であることから，$K$ の値は $1$ にしてしまいましょう。

さらに，$a=10$ のあたりで $T$ の値は $10$ と $100$ の間であることから，$1 < p < 2$ であることが予想されます。

最少二乗法で $p$ の値を求めてみます。

In [196]:
load(lsquares)$
In [197]:
M: read_matrix("planets.dat")$
f(x):=x^p;
fpprintprec: 3$
lsquares_estimates(M, [x, y], y=f(x), [ p])$
float(%);

*************************************************
  N=    1   NUMBER OF CORRECTIONS=25
       INITIAL VALUES
 F=  7.348237574827267D+03   GNORM=  1.077154642132768D+04
*************************************************

   I  NFN     FUNC                    GNORM                   STEPLENGTH

   1    5     1.904584801099601D+02   8.784310860959597D+03   4.246074778576236D-05  
   2    9     3.013015441521753D+00   1.225806729503201D+03   1.762944016428666D-02  
   3   10     3.124210853388047D-01   3.072692435748910D+02   1.000000000000000D+00  
   4   11     1.392523639450161D-01   7.671176899006442D+00   1.000000000000000D+00  
   5   12     1.391434699033869D-01   4.629018333594104D-02   1.000000000000000D+00  
   6   13     1.391434659389219D-01   7.036353104518235D-06   1.000000000000000D+00  

 THE MINIMIZATION TERMINATED WITHOUT DETECTING ERRORS.
 IFLAG = 0
Out[197]:
\[\tag{${\it \%o}_{273}$}f\left(x\right):=x^{p}\]
Out[197]:
\[\tag{${\it \%o}_{276}$}\left[ \left[ p=1.5 \right] \right] \]
In [198]:
fit: ev(f(x), %);
Out[198]:
\[\tag{${\it \%o}_{277}$}x^{1.5}\]

$\displaystyle T = a^{1.5}$ のような関係が得られました。

実際のケプラーの第3法則も，$T \propto a^{1.5}$ すなわち，$\displaystyle T^2 \propto a^3$ です。

In [199]:
plot2d([[discrete, dat], fit], [x, 0.1, 100],
       [style, [points, 1.5, red], [lines, 1, blue]], grid2d, logx, logy, 
       [gnuplot_preamble, "set key top left"], [legend, "惑星データ", "T = a^{1.5}"],
       [xlabel, "軌道長半径 a"], [ylabel, "公転周期 T"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 公転周期 T 軌道長半径 a 惑星データ 惑星データ T = a^{1.5} T = a^{1.5} 0.01 0.1 1 10 100 1000 0.1 1 10 100

リストと行列の成分

各惑星のデータは，

dat: read_nested_list("planets.dat")$
M: read_matrix("planets.dat")$

として既に読み込んでいました。

リストか行列かによって，成分の取り出し方は微妙に違います。

In [200]:
dat[1];  dat[1][1];
M[1];    M[1,1];

/* args 関数で行列をリストに変換できるのでしたね。 */
args(M)[1];  args(M)[1][1];
Out[200]:
\[\tag{${\it \%o}_{279}$}\left[ 0.384 , 0.241 \right] \]
Out[200]:
\[\tag{${\it \%o}_{280}$}0.384\]
Out[200]:
\[\tag{${\it \%o}_{281}$}\left[ 0.384 , 0.241 \right] \]
Out[200]:
\[\tag{${\it \%o}_{282}$}0.384\]
Out[200]:
\[\tag{${\it \%o}_{283}$}\left[ 0.384 , 0.241 \right] \]
Out[200]:
\[\tag{${\it \%o}_{284}$}0.384\]

惑星の公転運動

簡単のために，惑星（および冥王星）を離心率 $e=0$ の円軌道として，地球がちょうど1周する間に他の惑星がどれだけ公転運動するかを描いてみます。

半径 $a_i$，公転周期 $T_i$ の天体の $t=0$ での初期位置を $x$ 軸上として，時刻 $t$ における位置は

$$x = a_i \cos \frac{2\pi t}{T_i} = a_i \cos \omega_i\ t, \quad y = a_i \sin \frac{2\pi t}{T_i} = a_i \sin \omega_i\ t$$

です。

In [201]:
a(i):= M[i,1]$
T(i):= M[i,2]$
omega(i):= 2*float(%pi)/T(i)$

x(i,t):= a(i)*cos(omega(i)*t);
y(i,t):= a(i)*sin(omega(i)*t);
Out[201]:
\[\tag{${\it \%o}_{288}$}x\left(i , t\right):=a\left(i\right)\,\cos \left(\omega\left(i\right)\,t\right)\]
Out[201]:
\[\tag{${\it \%o}_{289}$}y\left(i , t\right):=a\left(i\right)\,\sin \left(\omega\left(i\right)\,t\right)\]

まずは地球の公転軌道を描きます。

In [202]:
plot2d([parametric, x(3, t), y(3, t), [t, 0, T(3)]], [xlabel,""], [ylabel,""],
       [gnuplot_preamble,"set key top left"],
       [legend, "地球"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 地球 地球 -1 -0.5 0 0.5 1 -1 -0.5 0 0.5 1

地球の公転軌道が円にみえるように調整し，他の惑星の軌道もあわせて描きます。

In [203]:
plot2d([[parametric, x(3, t), y(3, t), [t, 0, T(3)]],
        [parametric, x(4, t), y(4, t), [t, 0, T(3)]],
        [parametric, x(5, t), y(5, t), [t, 0, T(3)]], 
        [parametric, x(6, t), y(6, t), [t, 0, T(3)]]
       ], 
       [x, -2, 10], [y, -2, 4], [yx_ratio, 0.5], 
       [legend, "地球", "火星", "木星", "土星"], [gnuplot_preamble,"set key top left"],
       [xlabel,""], [ylabel,""] )$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 地球 地球 火星 火星 木星 木星 土星 土星 -2 -1 0 1 2 3 4 -2 0 2 4 6 8 10

練習

（練習）

  1. 残りの天体の軌道も描いてみましょう。
  2. GIF アニメにしてみましょう。
  3. 一番内側の水星がちょうど一周する時間に，残りの天体はどこまで運動するかがわかるように描いてみましょう。

人口問題

【参考】 「微分方程式で数学モデルを作ろう バージェス，ボリー著，日本評論社」

マルサスの人口モデル

人口変化のしかたを明らかにし，将来の変化を予測するモデルを定式化するこ とは実社会において非常に重要な問題である。ここでは，まずマルサスの 「人口論」に書かれたアイデアを紹介する。

時刻 $t$ におけるある国の総人口を $N(t)$ とする。短い時間間隔 $dt$ における 出生数と死亡数は，ともにその時点での総人口と時間間隔に比例するから，

$$\mbox{出生数} = \alpha N dt, \quad \mbox{死亡数} = \beta N dt $$

したがって，時間間隔$dt$での人口の増加$dN$は

$$dN = \alpha N dt - \beta N dt = \gamma N dt, \quad\mbox{ただし}\ \gamma \equiv \alpha - \beta $$

これは微分方程式

$$\frac{dN}{dt} = \gamma N $$

であり，次のように解ける。

In [204]:
ode2('diff(N, t) = gamma * N, N, t)$
ic1(%, t = t[0], N = N[0]);
Out[204]:
\[\tag{${\it \%o}_{293}$}N=N_{0}\,e^{t\,\gamma-t_{0}\,\gamma}\]

つまり， $$N(t) = N_0 \,e^{\gamma (t - t_0)} $$

ここで，$N_0 = N(t_0)$ は $t_0$ 年の人口である。また，$\gamma$ は，$t_0$ 年と $t_1$ 年の人口を使って以下のように求めることができる。

$$ \gamma = \frac{1}{t_1 - t_0} \ln\left(\frac{N(t_1)}{N_0} \right)$$

参考文献にあった，米国の人口データをファイルにしてあるので，これを読み込み，グラフに描きます。

In [205]:
usa: read_matrix("usa.dat")$
In [206]:
plot2d([discrete, args(usa)], 
       [style, [points, 1.5]], grid2d,
       [xlabel,"年"], [ylabel, "人口（単位：百万人）"],
       [gnuplot_preamble, "set key top left"],
       [legend, "米国の人口"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 人口（単位：百万人） 年 米国の人口 米国の人口 0 20 40 60 80 100 120 140 1780 1800 1820 1840 1860 1880 1900 1920 1940

人口データから，$t_0, N_0, \gamma$ の値を求め，マルサスモデル $N(t) = N_0 \,e^{\gamma (t - t_0)}$ を重ねて描きます。

In [207]:
t0: usa[1,1]$
N0: usa[1,2]$ 
gamma: 1/(usa[2,1]-usa[1,1])*log(usa[2,2]/usa[1,2])$
Nm(t):= N0*exp(gamma*(t-t0));
Out[207]:
\[\tag{${\it \%o}_{299}$}{\it Nm}\left(t\right):=N_{0}\,\exp \left(\gamma\,\left(t-t_{0}\right)\right)\]
In [208]:
plot2d([[discrete, args(usa)], Nm(t)], [t, 1780, 1940],
       [style, [points, 1.5], lines], grid2d,
       [xlabel,"年"], [ylabel, "人口（単位：百万人）"],
       [gnuplot_preamble, "set key top left"],
       [legend, "米国の人口", "マルサスモデル"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 人口（単位：百万人） 年 米国の人口 米国の人口 マルサスモデル マルサスモデル 0 50 100 150 200 250 300 350 400 1780 1800 1820 1840 1860 1880 1900 1920 1940

ヴェアフルストによる修正モデル

マルサス・モデルは，$\gamma > 0$ の場合には人口の際限ない増加を予測する。 しかし，実際には食糧資源の供給不足，人口の過密，その他の環境的要因によ り，このような無制限な増加は続かない。

ヴェアフルストは，人口過密の要因を考慮にいれて，次のような修正を提案し た。人口は継続し続ける限り増加するが，上限 (それを$N_{\max}$としよう) があるとする。そして，人口変化は，次の各々に比例すると仮定する:

  1. 現在の人口 $N$
  2. 未使用の人口資源に対する割合 $(1 - N/N_{\rm max})$

したがって微分方程式は

$$ \frac{dN}{dt} = \gamma N \left(1 - \frac{N}{N_{\rm max}}\right) $$

となり，（変数分離法によってこの式は解けて）解は

$$ N(t) = N_0 \frac{N_{\rm max}}{N_0 + (N_{\rm max}-N_0)\,e^{-\gamma (t-t_0)}} $$

パラメータ $N_{\max}$ をどのように選ぶと，米国の人口変化をよく再現するか，調べてみます。

In [209]:
t0: usa[1,1]$
N0: usa[1,2]$ 
gamma: 1/(usa[2,1]-usa[1,1])*log(usa[2,2]/usa[1,2])$

Nv(t):= N0*Nmax/(N0 + (Nmax - N0)*exp(-gamma*(t-t0)));
Out[209]:
\[\tag{${\it \%o}_{304}$}{\it Nv}\left(t\right):=\frac{N_{0}\,{\it Nmax}}{N_{0}+\left({\it Nmax}-N_{0}\right)\,\exp \left(\left(-\gamma\right)\,\left(t-t_{0}\right)\right)}\]
In [210]:
fpprintprec: 8$
lsquares_estimates(usa, [t, y], y = Nv(t), [Nmax])$
float(%);
Out[210]:
\[\tag{${\it \%o}_{307}$}\left[ \left[ {\it Nmax}=214.10557 \right] \right] \]
In [211]:
fit: Nv(t), %;
Out[211]:
\[\tag{${\it \%o}_{308}$}\frac{835.01172}{210.20557\,e^ {- 0.030673027\,\left(t-1790\right) }+3.9}\]
In [212]:
plot2d([[discrete, args(usa)], Nm(t), fit], [t, 1780, 1940],
       [style, [points, 1.5], lines, [lines, 2, blue]], grid2d,
       [xlabel,"年"], [ylabel, "人口（単位：百万人）"],
       [gnuplot_preamble, "set key top left"],
       [legend, "米国の人口", "マルサスモデル", "ヴェアフルストモデル"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 人口（単位：百万人） 年 米国の人口 米国の人口 マルサスモデル マルサスモデル ヴェアフルストモデル ヴェアフルストモデル 0 50 100 150 200 250 300 350 400 1780 1800 1820 1840 1860 1880 1900 1920 1940

フーリエ級数展開

周期$2L$の周期関数$f(x)$のフーリエ級数展開は

$$ f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty}\left( a_n \cos\frac{n\pi x}{L} + b_n \sin \frac{n\pi x}{L}\right) $$

ここで，フーリエ係数 $a_n, b_n$ は以下のように求めるのであった。

$$ a_n = \frac{1}{L} \int_{-L}^{L} f(x)\cos\frac{n\pi x}{L}\, dx, \quad b_n = \frac{1}{L} \int_{-L}^{L} f(x)\sin\frac{n\pi x}{L}\, dx. $$

矩形波のフーリエ級数展開

以下のように $\pi \le x < \pi$ で定義された矩形が，この領域外では周期 $2\pi$ の矩形波となっている例。

$$ f(x) = \left\{ \begin{array}{rl} -1 & \mbox{$(-\pi \le x < 0)$} \\ 1 & \mbox{$(0 \le x < \pi)$} \end{array} \right. $$

Maxima でこの周期的矩形波をどうやって表すかが，工夫のしどころ。

私としては，以下を提案する。

$$ f(x) = \mbox{signum}(\sin x) $$

ここで，$\mbox{signum}(x)$ は，$x>0$ のとき $+1$，$x<0$ のとき $-1$ を返す関数。

In [213]:
f(x):= signum(sin(x));
Out[213]:
\[\tag{${\it \%o}_{310}$}f\left(x\right):={\it signum}\left(\sin x\right)\]
In [214]:
plot2d(f(x), [x, -2*%pi, 2*%pi], [y, -1.5, 1.5], [xtics, %pi], grid2d, [ylabel,""],
[gnuplot_preamble, "set format x '%4.1P π'"], 
[legend,"f(x)"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x f(x) f(x) -1.5 -1 -0.5 0 0.5 1 1.5 -2.0 π -1.0 π 0.0 π 1.0 π 2.0 π

$f(x)$ は奇関数なので，フーリエ係数は $b_n$ のみ。

In [215]:
b(n):= 1/%pi * integrate((-1)*sin(n*x), x, -%pi, 0) 
     + 1/%pi * integrate((+1)*sin(n*x), x, 0, %pi)$

Fourier(n, x):= sum(b(i)*sin(i*x), i, 1, n)$
In [216]:
for i:1 thru 9 do print("b[", i, "] = ", b(i) );
b[ \(1\) ] = \(\frac{4}{\pi}\)
b[ \(2\) ] = \(0\)
b[ \(3\) ] = \(\frac{4}{3\,\pi}\)
b[ \(4\) ] = \(0\)
b[ \(5\) ] = \(\frac{4}{5\,\pi}\)
b[ \(6\) ] = \(0\)
b[ \(7\) ] = \(\frac{4}{7\,\pi}\)
b[ \(8\) ] = \(0\)
b[ \(9\) ] = \(\frac{4}{9\,\pi}\)
Out[216]:
\[\tag{${\it \%o}_{314}$}\mathbf{done}\]
In [217]:
plot2d([f(x), Fourier(1,x)],  
       [x, -2*%pi, 2*%pi], [y, -1.5, 2], [xtics, %pi], grid2d, [ylabel,""],
       [style, lines, [lines, 3, red]],
       [gnuplot_preamble, "set format x '%4.1P π'"], 
       [legend,"f(x)", "n = 1"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x f(x) f(x) n = 1 n = 1 -1.5 -1 -0.5 0 0.5 1 1.5 2 -2.0 π -1.0 π 0.0 π 1.0 π 2.0 π
In [218]:
plot2d([f(x), Fourier(1,x), Fourier(3,x)],  
       [x, -2*%pi, 2*%pi], [y, -1.5, 2], [xtics, %pi], grid2d, [ylabel,""],
       [style, lines, [dots, gray], [lines, 2, red]],
       [gnuplot_preamble, "set format x '%4.1P π'"], 
       [legend,"f(x)", "", "n = 3"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x f(x) f(x) gnuplot_plot_2 n = 3 n = 3 -1.5 -1 -0.5 0 0.5 1 1.5 2 -2.0 π -1.0 π 0.0 π 1.0 π 2.0 π
In [219]:
plot2d([f(x), Fourier(1,x), Fourier(3,x), Fourier(5,x)],  
       [x, -2*%pi, 2*%pi], [y, -1.5, 2], [xtics, %pi], grid2d, [ylabel,""],
       [style, lines, [dots, gray], [dots, gray], [lines, 3, red]],
       [gnuplot_preamble, "set format x '%4.1P π'"], 
       [legend,"f(x)", "", "", "n = 5"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x f(x) f(x) gnuplot_plot_2 gnuplot_plot_3 n = 5 n = 5 -1.5 -1 -0.5 0 0.5 1 1.5 2 -2.0 π -1.0 π 0.0 π 1.0 π 2.0 π
In [220]:
plot2d([f(x), Fourier(1,x), Fourier(3,x), Fourier(5,x), Fourier(7,x)],  
       [x, -2*%pi, 2*%pi], [y, -1.5, 2], [xtics, %pi], grid2d, [ylabel,""],
       [style, lines, [dots, gray], [dots, gray], [dots, gray], [lines, 3, red]],
       [gnuplot_preamble, "set format x '%4.1P π'"], 
       [legend,"f(x)", "", "", "", "n = 7"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x f(x) f(x) gnuplot_plot_2 gnuplot_plot_3 gnuplot_plot_4 n = 7 n = 7 -1.5 -1 -0.5 0 0.5 1 1.5 2 -2.0 π -1.0 π 0.0 π 1.0 π 2.0 π

三角波のフーリエ級数展開

以下のように $\pi \le x < \pi$ で定義された三角形が，この領域外では周期 $2\pi$ の三角波となっている例。

$$ f(x) =\left\{ \begin{array}{rl} \pi + x, &\mbox{$(-\pi \le x < 0)$} \\ \pi - x, &\mbox{$(0 \le x < \pi)$} \end{array} \right. $$

Maxima でこの周期的三角波をどうやって表すかが，工夫のしどころ。

私としては，以下を提案する。

f(x):= abs(x - 2*%pi*floor(x/(2*%pi)) - %pi)

$$ f(x) = \left| x - 2\pi\,\mbox{floor}\left(\frac{x}{2\pi}\right) - \pi\right| $$
In [221]:
f(x):= abs(x - 2*%pi*floor(x/(2*%pi)) - %pi);
Out[221]:
\[\tag{${\it \%o}_{319}$}f\left(x\right):=\left| x-2\,\pi\,\left \lfloor \frac{x}{2\,\pi} \right \rfloor-\pi\right| \]
In [222]:
plot2d(f(x), 
    [x, -3*%pi, 3*%pi], [y, -0.2, 4], 
    [xtics, %pi], [ytics, 0.5*%pi], grid2d, [ylabel,""],
    [gnuplot_preamble, "set format x '%4.1P π'; set format y '%4.1P π'"], 
    [legend,"f(x)"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x f(x) f(x) 0.0 π 0.5 π 1.0 π -3.0 π -2.0 π -1.0 π 0.0 π 1.0 π 2.0 π 3.0 π

$f(x)$ は偶関数なので，フーリエ係数は $a_n$ のみ。

In [223]:
a(n):= 1/%pi * integrate((%pi + x)*cos(n*x), x, -%pi, 0) 
     + 1/%pi * integrate((%pi - x)*cos(n*x), x, 0, %pi)$

Fourier(n, x):= a(0)/2 + sum(a(i)*cos(i*x), i, 1, n)$
In [224]:
makelist(a(i), i, 0, 8);
Out[224]:
\[\tag{${\it \%o}_{323}$}\left[ \pi , \frac{4}{\pi} , 0 , \frac{4}{9\,\pi} , 0 , \frac{4}{25\,\pi} , 0 , \frac{4}{49\,\pi} , 0 \right] \]
In [225]:
plot2d([f(x), Fourier(1,x)],
    [x, -3*%pi, 3*%pi], [y, -0.2, 4], 
    [xtics, %pi], [ytics, 0.5*%pi], grid2d, [ylabel,""],
    [style, lines, [lines, 3, red]],
    [gnuplot_preamble, "set format x '%4.1P π'; set format y '%4.1P π'"], 
    [legend,"f(x)", "n = 1"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x f(x) f(x) n = 1 n = 1 0.0 π 0.5 π 1.0 π -3.0 π -2.0 π -1.0 π 0.0 π 1.0 π 2.0 π 3.0 π
In [226]:
plot2d([f(x), Fourier(1,x), Fourier(3,x)],
    [x, -3*%pi, 3*%pi], [y, -0.2, 4], 
    [xtics, %pi], [ytics, 0.5*%pi], grid2d, [ylabel,""],
    [style, lines, [dots, gray], [lines, 3, red]],
    [gnuplot_preamble, "set format x '%4.1P π'; set format y '%4.1P π'"], 
    [legend,"f(x)", "", "n = 3"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x f(x) f(x) gnuplot_plot_2 n = 3 n = 3 0.0 π 0.5 π 1.0 π -3.0 π -2.0 π -1.0 π 0.0 π 1.0 π 2.0 π 3.0 π
In [227]:
plot2d([f(x), Fourier(1,x), Fourier(3,x), Fourier(5,x)],
    [x, -3*%pi, 3*%pi], [y, -0.2, 4], 
    [xtics, %pi], [ytics, 0.5*%pi], grid2d, [ylabel,""],
    [style, lines, [dots, gray], [dots, gray], [lines, 3, red]],
    [gnuplot_preamble, "set format x '%4.1P π'; set format y '%4.1P π'"], 
    [legend,"f(x)", "", "", "n = 5"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x f(x) f(x) gnuplot_plot_2 gnuplot_plot_3 n = 5 n = 5 0.0 π 0.5 π 1.0 π -3.0 π -2.0 π -1.0 π 0.0 π 1.0 π 2.0 π 3.0 π
In [228]:
plot2d([f(x), Fourier(1,x), Fourier(3,x), Fourier(5,x), Fourier(7,x)],
    [x, -3*%pi, 3*%pi], [y, -0.2, 4], 
    [xtics, %pi], [ytics, 0.5*%pi], grid2d, [ylabel,""],
    [style, lines, [dots, gray], [dots, gray], [dots, gray], [lines, 3, red]],
    [gnuplot_preamble, "set format x '%4.1P π'; set format y '%4.1P π'"], 
    [legend,"f(x)", "", "",  "", "n = 7"])$
Gnuplot Produced by GNUPLOT 5.4 patchlevel 0 x f(x) f(x) gnuplot_plot_2 gnuplot_plot_3 gnuplot_plot_4 n = 7 n = 7 0.0 π 0.5 π 1.0 π -3.0 π -2.0 π -1.0 π 0.0 π 1.0 π 2.0 π 3.0 π